The given infinite grid consists of hexagonal cells of six resistors each of resistance R. then R12

R3
2R3
4R3
3R4
The correct Answer is:B
Here we will apply superposition principle.
i. Let feed a current I to point 1, but do not draw the current
from 2 and allow the currjent to spread to infinity. Then current
in branch 12 will be I/3
ii. Secondly, feed current I to the current at take it out from 2,
now again current through branch 12 will be I/3
iii. Now carry out both the above steps (i) and (ii) simultaneously.
Then current in branch 12 will be sum of above two currents,
i.e.,I3+I3=2I3
Resistance between 1 and 2 is R.
Let remaining resistance is R1
Then

R1I3=R2I3orR1=2R
Req=RR1R+R1=R2RR+2R=2R3
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Multiple Correct16videos
ELECTRIC CURRENT AND CIRCUIT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Comprehension35videos
ELECTRIC CURRENT AND CIRCUIT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Subjective29videos
ELECTRIC CURRENT AND CIRCUIT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT & CIRCUITSEXERCISE - Kirchhoff s law and simple circuits15videos
ELECTRIC CURRENT & CIRCUITS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s38videos
ELECTRIC FLUX AND GAUSS LAW
Similar Questions
The circuit shown in the figure above consists of eight resistors, each with resistance R, and a battery with terminal voltage V and negligible internal resistance. The current flowing through the battery is n4VR, then n is
 View Solution
View Solution(i) State the two Kirchhoff's laws, Explain of the briefly how these rules are justified.
(ii) The current is drawn from a cell of emf E andinternal resistance r connected to the network of resistors each of resistance r as shown in the figure. Obtain the expression for (i) The current draw from the cell and (ii) the power consumed in the network .
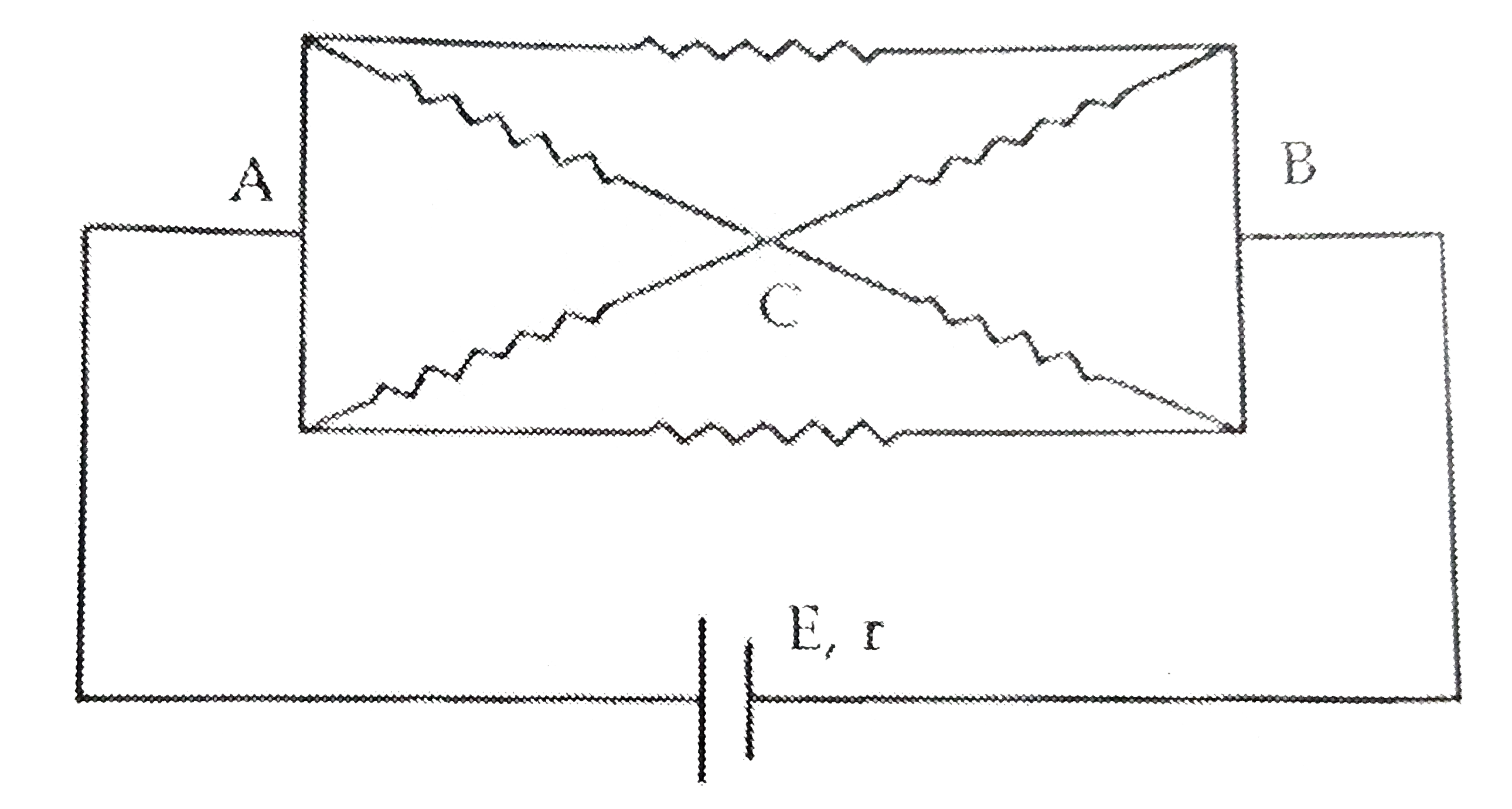 View Solution
View SolutionIn the given circuit, if resistance of each resistor is R:

Find the equivalent resistance between M and N,View SolutionIn the given circuit, if resistance of each resistor is R:
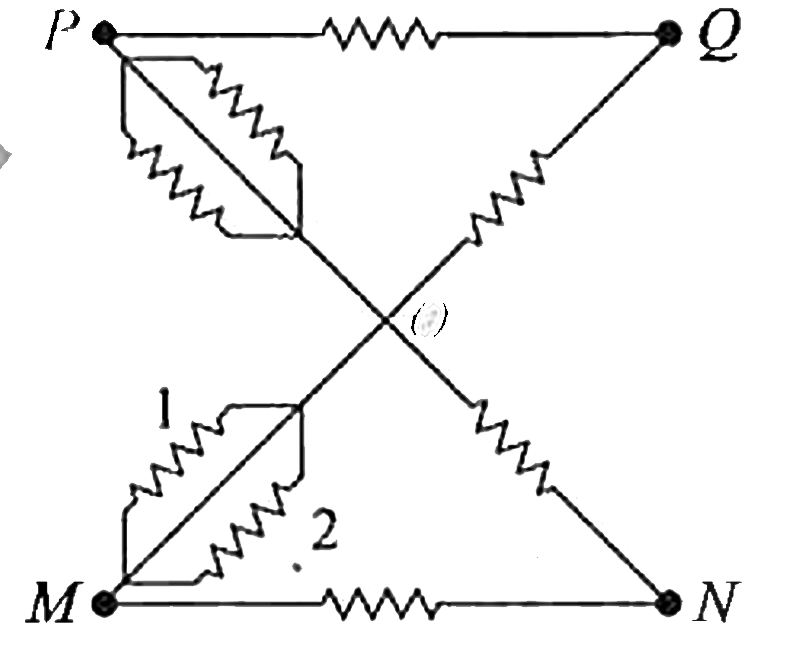
The equivalent resistance between M and Q.View SolutionFind the equivalent resistance between terminals A and B. Each resistor is of resistance R.
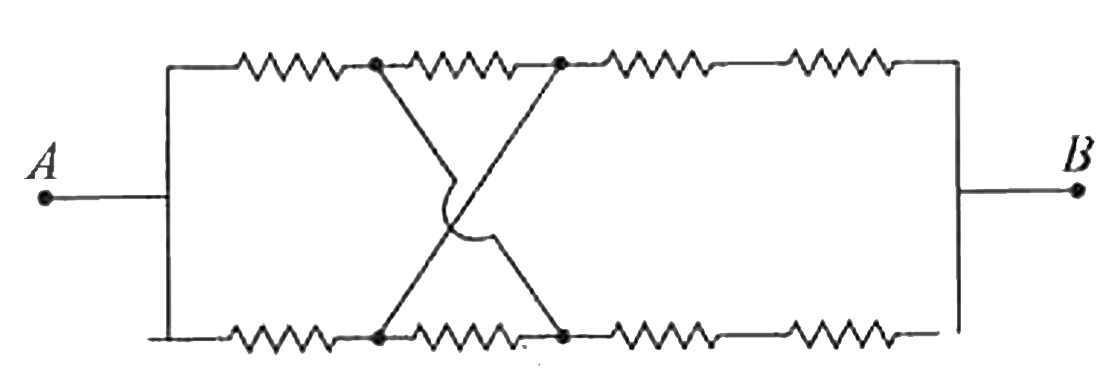 View Solution
View SolutionIn the circuit shown, both cells are ideal and of fixed emf, the resistance of resistance R1 has fixed resistance and the resistance of resistor R2 can be varied (but the value of R2 is not zero). Then:
 View Solution
View SolutionThe circuit consists of two resistors (of resistance R1=20Ω and R2=10Ω), a capacitor (of capacitance C=10μF) and two ideal cells. In the circuit shown the capacitor is in steady state and the switch S is open

The current through the resistor R2 just after the switch S is closed is :View SolutionThe maximum and the minimum equivalent resistance obtained by combining n identical resistors of resistance R, are RmaxandRmin respectively. The ratio RmaxRmin is equal to
View SolutionThe circuit consists of two resistors (of resistance R1=20Ω and R2=10Ω), a capacitor (of capacitance C=10μF) and two ideal cells. In the circuit shown the capacitor is in steady state and the switch S is open
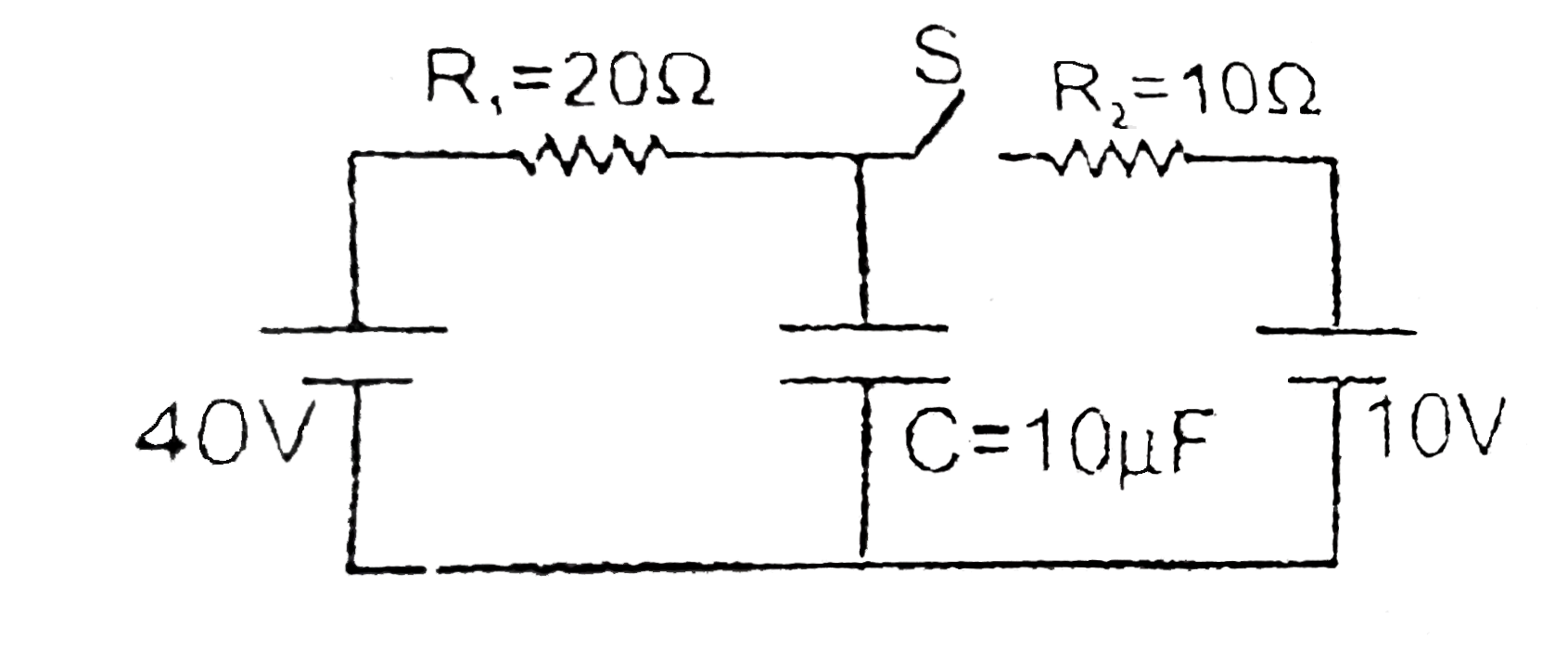
The charge on capacitor in steady state with switch S closed.View SolutionA combination consists of three resistors in series. Four similar sets are connected in parallel. If the resistance of each resistor is 2 Ω, find the resistance of the combination.
View Solution

