A nonuniformly charged ring is kept near an uncharged conducting solid sphere. The distance between their centres (which are on the same line normal to the plane of the ring) is 3m and their radius is 4m. If total charge on the ring is 1μC, then the potential of the sphere will be
2.25kV
3kV
1.8kV
cannot be determined
The correct Answer is:C
To solve the problem, we need to find the potential of an uncharged conducting solid sphere when placed near a nonuniformly charged ring. Here are the steps to arrive at the solution:
Step 1: Understand the Configuration
We have a nonuniformly charged ring with a total charge Q=1μC=1×10−6C and a conducting solid sphere that is uncharged. The distance between the centers of the ring and the sphere is d=3m, and the radius of the ring is R=4m.
Step 2: Determine the Distance from the Ring to the Sphere
Since the distance between the centers is given as 3m and the radius of the ring is 4m, we can visualize that the closest point of the ring to the sphere is at a distance of d−R=3m−4m=−1m. However, this indicates that the ring is actually further away from the sphere than its radius, so we will consider the distance from the center of the ring to the surface of the sphere.
Step 3: Calculate the Effective Distance
The effective distance from the ring to the surface of the sphere is:
D=d+R=3m+4m=7m
Step 4: Use the Formula for Electric Potential
The potential V at a point due to a point charge is given by:
V=14πϵ0⋅Qr
where r is the distance from the charge to the point where the potential is being calculated, and ϵ0 is the permittivity of free space, approximately 8.85×10−12C2/(N⋅m2).
Step 5: Substitute Values into the Formula
Substituting Q=1×10−6C and r=7m:
V=14π(8.85×10−12)⋅1×10−67
Step 6: Calculate the Numerical Value
Calculating 14π(8.85×10−12):
14π(8.85×10−12)≈9×109N⋅m2/C2
Now substituting this into the potential formula:
V≈9×109⋅1×10−67≈9×1037≈1285.71V
Step 7: Convert to Kilovolts
To express the potential in kilovolts:
V≈1.28571kV≈1.29kV
Conclusion
The potential of the sphere due to the charged ring is approximately 1.29 kV.
We have a nonuniformly charged ring with a total charge Q=1μC=1×10−6C and a conducting solid sphere that is uncharged. The distance between the centers of the ring and the sphere is d=3m, and the radius of the ring is R=4m.
Since the distance between the centers is given as 3m and the radius of the ring is 4m, we can visualize that the closest point of the ring to the sphere is at a distance of d−R=3m−4m=−1m. However, this indicates that the ring is actually further away from the sphere than its radius, so we will consider the distance from the center of the ring to the surface of the sphere.
The effective distance from the ring to the surface of the sphere is:
D=d+R=3m+4m=7m
The potential V at a point due to a point charge is given by:
V=14πϵ0⋅Qr
where r is the distance from the charge to the point where the potential is being calculated, and ϵ0 is the permittivity of free space, approximately 8.85×10−12C2/(N⋅m2).
Substituting Q=1×10−6C and r=7m:
V=14π(8.85×10−12)⋅1×10−67
Calculating 14π(8.85×10−12):
14π(8.85×10−12)≈9×109N⋅m2/C2
Now substituting this into the potential formula:
V≈9×109⋅1×10−67≈9×1037≈1285.71V
To express the potential in kilovolts:
V≈1.28571kV≈1.29kV
The potential of the sphere due to the charged ring is approximately 1.29 kV.
Topper's Solved these Questions
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Assertion and Reason Type
8 Videos
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Comprehension Type
94 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Multiple Correct Answer type
2 Videos
- MISCELLANEOUS VOLUME 5BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Integer
12 Videos
Similar Questions
An electric dipole is kept on the axis of a uniformly charged ring at distance from the centre of the ring. The direction of the dipole moment is along the axis. The dipole moment is p, charge of the ring is Q & radius of the ring is R. The force on the dipole is
View SolutionA conducting shell S1 having a charge Q is surrounded by an uncharged concentric conducting spherical shell S2.
Let the potential difference between S1 and that S2 be V. If the shell S2 is now given a charge −3Q, the new potential difference between the same two shells is
View SolutionAn isolated conduction sphere sphere whose radius R=1 m has a charge q=19nC. The energy density at the surfasce of the sphere is
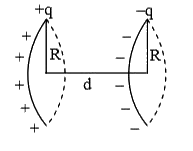
View SolutionTwo thin rings each of radius R are placed at a distance 'd' apart. The charges on the rings are +q and -q. The potential difference between their centres will be -
View SolutionA hollow metallic sphere of radius 0.1 m is charged to a potential of 5 V. The potential at its centre is
View SolutionA non-conducting solid sphere of radius R is uniformly charged. The magnitude of the electric filed due to the sphere at a distance r from its centre
View SolutionFor a uniformly charged non conducting sphere of radius R which of following shows a correct graph between the electric field intensity and the distance from the centre of sphere –
View SolutionAssertion: A positively charged rod is held near a neutral conducting solid sphere as illustrated below. The sphere lies on a insulated stand. The potential of ground (or earth) is zero. The potential at point A (point A need not be centre of the sphere) is higher compared to potential of gound (earth).
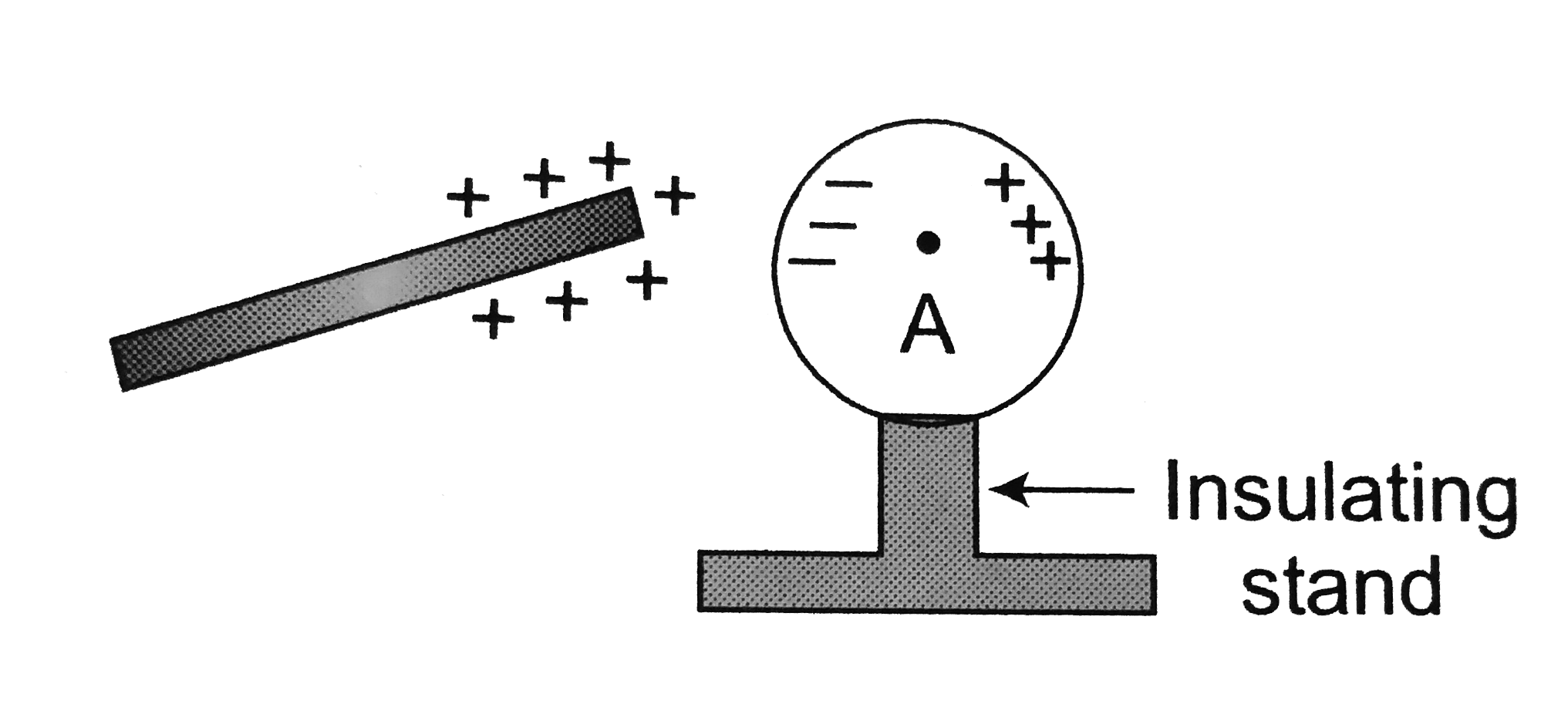
Reason: In this situation of assertion, the potential at the centre of conducting sphere is positive. the solid sphere being conducting, potential at each point in the sphere is same.
View SolutionAssertion: A positively charged rod is held near a neutral conducting solid sphere as illustrated below. The sphere lies on a insulated stand. The potential of ground (or earth) is zero. The potential at point A (point A need not be centre of the sphere) is higher compared to potential of gound (earth).

Reason: In this situation of assertion, the potential at the centre of conducting sphere is positive. the solid sphere being conducting, potential at each point in the sphere is same.
View SolutionBoth the ring and the conducting sphere are given the same charge Q. Determine the potential of the sphere. Assume that the centre of the sphere lies on the axis of th ring. Is it necessary that the charge on the ring be uniformly distributed to answer the above question ?
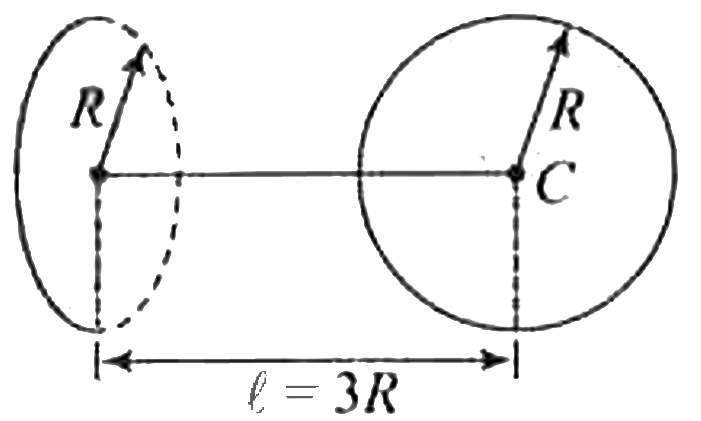
View Solution
