A charge is fixed at the origin of the co-ordinate system while a small electric dipole of dipolement pointing away from the charge along the x-axis is set free from a point far away from the origin.
(a) Calculate the K.E. of the dipole when it reaches to a point (d, 0).
(b) Calculate the force on the charge at this moment.
To solve the problem, we will break it down into two parts as specified in the question.
Part (a): Calculate the K.E. of the dipole when it reaches a point (d, 0).
1. Understanding the Potential Due to the Dipole:
The potential V due to an electric dipole at a distance r is given by:
V=14πϵ0→p⋅^rr2
where →p is the dipole moment, ^r is the unit vector in the direction from the dipole to the point where the potential is being calculated, and r is the distance from the dipole.
2. Calculating the Potential at Infinity:
At a point far away (infinity), the potential V∞ due to the dipole is zero:
V∞=0
3. Calculating the Potential at Point (d, 0):
At the point (d, 0), the angle θ between the dipole moment and the line joining the dipole to the charge is 180 degrees (since the dipole is pointing away from the charge). Therefore, cos(180∘)=−1:
Vd=14πϵ0p⋅(−1)d2=−p4πϵ0d2
4. Finding the Change in Potential:
The change in potential ΔV as the dipole moves from infinity to the point (d, 0) is:
ΔV=Vd−V∞=−p4πϵ0d2−0=−p4πϵ0d2
5. Calculating the Kinetic Energy:
The kinetic energy (K.E.) gained by the dipole as it moves from infinity to the point (d, 0) can be calculated using the formula:
KE=q⋅ΔV
Substituting ΔV:
KE=q(−p4πϵ0d2)=−qp4πϵ0d2
Since kinetic energy cannot be negative, we take the absolute value:
KE=qp4πϵ0d2
Part (b): Calculate the force on the charge +Q at this moment.
1. Electric Field Due to the Dipole:
The electric field E due to a dipole at a distance d along the axis of the dipole is given by:
E=14πϵ02pd3
2. Calculating the Force on Charge +Q:
The force F experienced by the charge +Q in the electric field E is given by:
F=Q⋅E
Substituting the expression for E:
F=Q⋅(14πϵ02pd3)=2Qp4πϵ0d3
Summary of Results:
- (a) The kinetic energy of the dipole at point (d, 0) is:
KE=qp4πϵ0d2
- (b) The force on the charge +Q at this moment is:
F=2Qp4πϵ0d3
The potential V due to an electric dipole at a distance r is given by:
V=14πϵ0→p⋅^rr2
where →p is the dipole moment, ^r is the unit vector in the direction from the dipole to the point where the potential is being calculated, and r is the distance from the dipole.
At a point far away (infinity), the potential V∞ due to the dipole is zero:
V∞=0
At the point (d, 0), the angle θ between the dipole moment and the line joining the dipole to the charge is 180 degrees (since the dipole is pointing away from the charge). Therefore, cos(180∘)=−1:
Vd=14πϵ0p⋅(−1)d2=−p4πϵ0d2
The change in potential ΔV as the dipole moves from infinity to the point (d, 0) is:
ΔV=Vd−V∞=−p4πϵ0d2−0=−p4πϵ0d2
The kinetic energy (K.E.) gained by the dipole as it moves from infinity to the point (d, 0) can be calculated using the formula:
KE=q⋅ΔV
Substituting ΔV:
KE=q(−p4πϵ0d2)=−qp4πϵ0d2
Since kinetic energy cannot be negative, we take the absolute value:
KE=qp4πϵ0d2
The electric field E due to a dipole at a distance d along the axis of the dipole is given by:
E=14πϵ02pd3
The force F experienced by the charge +Q in the electric field E is given by:
F=Q⋅E
Substituting the expression for E:
F=Q⋅(14πϵ02pd3)=2Qp4πϵ0d3
- (a) The kinetic energy of the dipole at point (d, 0) is:
KE=qp4πϵ0d2
- (b) The force on the charge +Q at this moment is:
F=2Qp4πϵ0d3
Topper's Solved these Questions
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Interger Answer type
20 Videos
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Fill in the blanks
10 Videos
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Assertion and Reason Type
8 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Multiple Correct Answer type
2 Videos
- MISCELLANEOUS VOLUME 5BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Integer
12 Videos
Similar Questions
A positive point charge q is fixed at origin. A dipole with a dipole momen →p is placed along the x-axis for away from the orgin with →p poiniting along positive x-axis .
(i) If the kinetic energy of the diople when it reachers a distance d from the origin is qp4πε0dn, then n is .
(ii) If the force experienced by the charge q at this moment is 4qpπε0d3,ˆi then x is.
View SolutionAn electric dipole is placed at the origin O and is directed along the x-axis. At a point P, far away from the dipole, the electric field is parallel to y-axis. OP makes an angle θ with the x-axis then
View SolutionAn electric dipole is placed at the origin O and is directed along the x-axis. At a point P, far away from the dipole, the electric field is parallel to y-axis. OP makes an angle θ with the x-axis then
View SolutionAn electric dipole consists of two charges of equal magnitude and opposite sign separately by a distance 2a. The dipole is along the X-axis and is centred at the origin
(i) Calculate the electric potential at point P
(ii) Calculate V at a point far from the dipole.
View SolutionA point charge q is placed at the origin . How does the electric field due to the charge very with distance r from the origin ?
View SolutionA small electric dipole is placed at origin with its dipole moment directed along positive x-axis .The direction of electric field at point (2,2√2,0)
View SolutionThe electric field of an electric dipole at a point on its axis , at a distance d from the centre of the dipole, varies as
View SolutionA short electric dipole is placed at a distance x from centre O on the axis of a ring of radius R and charge Q is uniformly distributed over tis.

The net force acting on the dipole will be
View SolutionAn electric dipole consists of two charges of equal magnitude and opposite sign saperated by a distance 2 a as shown in figure . The dipole is along the x axis and is centered at the origin
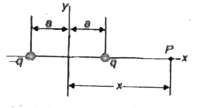
(A) Calculate the electric potential at point P .
(B ) Calculate V at a point far from the dipole .
View SolutionAn electric dipole is fixed at the origin of coordinates. Its moment is directed in the positive x- direction. A positive charge is moved from the point (r,0) to the point (−r,0) by an external agent. In this process, the work done by the agent is
View Solution
