Consider a resistor of uniform cross-sectional area connected to a battery of internal resistance zero. If the length of the resistor is doubled by stretching it, then
the current will become four times
the electric field in the wire will become half
the thermal power produced by the resistor will become one fourth
The product of the current density and conductance will become half.
The correct Answer is:B, C
To solve the problem, we need to analyze the effects of doubling the length of a resistor while keeping its volume constant. Here’s a step-by-step breakdown of the solution:
Step 1: Understand the relationship between resistance, length, and area
The resistance R of a uniform resistor is given by the formula:
R=ρLA
where:
- R is the resistance,
- ρ is the resistivity of the material,
- L is the length of the resistor,
- A is the cross-sectional area.
Step 2: Determine the new dimensions after stretching
When the length of the resistor is doubled, we have:
L′=2L
Since the volume V of the resistor remains constant, we can express the volume as:
V=A⋅L
After stretching, the new volume is:
V′=A′⋅L′=A′⋅(2L)
Setting the volumes equal gives:
A⋅L=A′⋅(2L)
From this, we can solve for the new area A′:
A′=A2
Step 3: Calculate the new resistance
Now we can substitute L′ and A′ into the resistance formula:
R′=ρL′A′=ρ(2L)A2=2ρL⋅2A=4ρLA=4R
Thus, the new resistance R′ is four times the original resistance R.
Step 4: Analyze the current through the resistor
Using Ohm's law, the current I through the resistor is given by:
I=ER
where E is the electromotive force (emf) of the battery. The new current I′ through the modified resistor is:
I′=ER′=E4R=I4
This indicates that the new current is one-fourth of the original current.
Step 5: Determine the electric field in the wire
The electric field E in the wire can be expressed as:
E=VL
For the new wire, the electric field E′ becomes:
E′=VL′=V2L=E2
Thus, the electric field in the wire is halved.
Step 6: Calculate the thermal power produced by the resistor
The power P dissipated in the resistor is given by:
P=V2R
For the new resistor, the power P′ is:
P′=V2R′=V24R=P4
This shows that the thermal power produced by the resistor is also one-fourth of the original power.
Step 7: Analyze the product of current density and conductance
The current density J is given by:
J=IA
And the conductance G is the reciprocal of resistance:
G=1R
The product of current density and conductance JG is:
JG=IA⋅1R
Since both current and area have changed, we need to analyze how they affect the product. However, since the resistivity and geometry have changed in a way that keeps the product constant, we conclude that JG remains unchanged.
Summary of Results
1. The new resistance R′=4R.
2. The new current I′=I4.
3. The electric field E′=E2.
4. The thermal power P′=P4.
5. The product of current density and conductance remains constant.
The resistance R of a uniform resistor is given by the formula:
R=ρLA
where:
- R is the resistance,
- ρ is the resistivity of the material,
- L is the length of the resistor,
- A is the cross-sectional area.
When the length of the resistor is doubled, we have:
L′=2L
Since the volume V of the resistor remains constant, we can express the volume as:
V=A⋅L
After stretching, the new volume is:
V′=A′⋅L′=A′⋅(2L)
Setting the volumes equal gives:
A⋅L=A′⋅(2L)
From this, we can solve for the new area A′:
A′=A2
Now we can substitute L′ and A′ into the resistance formula:
R′=ρL′A′=ρ(2L)A2=2ρL⋅2A=4ρLA=4R
Thus, the new resistance R′ is four times the original resistance R.
Using Ohm's law, the current I through the resistor is given by:
I=ER
where E is the electromotive force (emf) of the battery. The new current I′ through the modified resistor is:
I′=ER′=E4R=I4
This indicates that the new current is one-fourth of the original current.
The electric field E in the wire can be expressed as:
E=VL
For the new wire, the electric field E′ becomes:
E′=VL′=V2L=E2
Thus, the electric field in the wire is halved.
The power P dissipated in the resistor is given by:
P=V2R
For the new resistor, the power P′ is:
P′=V2R′=V24R=P4
This shows that the thermal power produced by the resistor is also one-fourth of the original power.
The current density J is given by:
J=IA
And the conductance G is the reciprocal of resistance:
G=1R
The product of current density and conductance JG is:
JG=IA⋅1R
Since both current and area have changed, we need to analyze how they affect the product. However, since the resistivity and geometry have changed in a way that keeps the product constant, we conclude that JG remains unchanged.
1. The new resistance R′=4R.
2. The new current I′=I4.
3. The electric field E′=E2.
4. The thermal power P′=P4.
5. The product of current density and conductance remains constant.
Topper's Solved these Questions
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Assertion and Reason
8 Videos
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Integer Answer Type
11 Videos
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Assertion-Reasoning Type
1 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Multiple Correct Answer type
2 Videos
- MISCELLANEOUS VOLUME 5BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Integer
12 Videos
Similar Questions
Statement I: A wire of uniform cross-section and uniform resistivity is connected across an ideal cell. Now the length of the wire is doubled keeping volume of the wire constant. The drift velocity of electrons after stretching the wire becomes one-fouth of what it was before stretching the wire.
Statement II: If a wire (of uniform resistivity and uniform cross section) of length l0 is stretched to length nl0, then its resistance becomes n2 times of what it was before stretching the wire (the volume of wire is kept constant in stretching process). Further at constant potential difference, current is inversely proportional to resistance. Finally, drift velocity of free electron is directly proportional to current and inversely proportional to cross-sectional area of current carrying wire.
View SolutionFirst a set of n equal resistors of R each are connected in series to a battery of emf E and internal resistance R. A current I is observed to flow. Then, the n resistors are connected in parallel to the same battery. It is observed that the current is increased 10 times. What is 'n'?
View SolutionA resistor of resistance R is connected to an ideal battery. If the value of R is decreased,the power dissipated in the resistor will
View SolutionA resistor of resistance R is connected to an ideal battery. If the value of R is decreased,the power dissipated in the resistor will
View SolutionA set of 'n' equal resistor, of value of 'R' each are connected in series to a battery of emf 'E' and internal resistance 'R'. The current drawn is I. Now, the 'n' resistors are connected in parallel to the same battery. Then the current drawn from battery becomes 10.1. The value of 'n' is
View SolutionTwo resistors of resistances 2Ωand4Ω when connected to a battery will have :
View SolutionThree resistors are connected to a 12 V battery as shown in the figure given below :

What is the current through the 8 ohm resistor ?
View SolutionThree resistors are connected to a 12 V battery as shown in the figure given below :
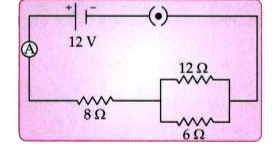
What is the current through the 6 ohm resistor ?
View SolutionIn the circuit shows in Fig. 6.42, resistors X and Y, each with resistance R, are connected to a 6V battery of negligible internal resistance. A voltmeter, also of resistance R, is connected across Y.
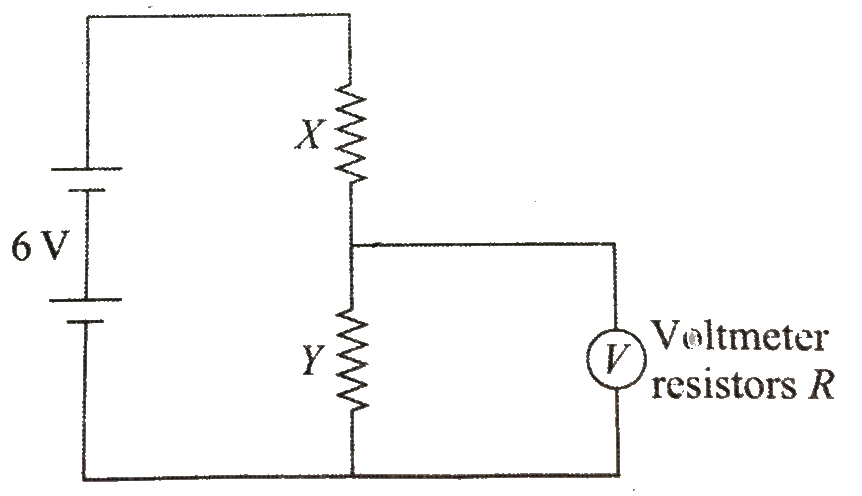
What is the reading of the voltmeter?
View SolutionThree resistors are connected to a 6 V battery as shown in the figure
Calculate:
potential difference across the 7.2 ohm resistor
View Solution
