A resistor of resistance R is connected to an ideal battery. If the value of R is decreased,the power dissipated in the resistor will
increase
decrease
remain unchanged
None of these
The correct Answer is:B
To solve the problem, we need to analyze how the power dissipated in a resistor changes when its resistance is decreased while connected to an ideal battery.
1. Understanding the Circuit:
- We have a resistor R connected to an ideal battery. An ideal battery provides a constant voltage (or EMF) E with no internal resistance.
2. Power Formula:
- The power P dissipated in a resistor can be calculated using the formula:
P=V2R
- Here, V is the voltage across the resistor, which is equal to the EMF E of the battery.
3. Initial Power Calculation:
- Initially, the power dissipated in the resistor R is:
P=E2R
4. Changing the Resistance:
- Now, if we decrease the resistance R to a new value R′ (where R′<R), the voltage across the resistor remains the same (still equal to E).
5. New Power Calculation:
- The new power P′ dissipated in the resistor R′ is:
P′=E2R′
6. Comparing Powers:
- Since R′<R, it follows that:
E2R′>E2R
- This implies that:
P′>P
- Therefore, the power dissipated in the resistor increases when the resistance is decreased.
7. Conclusion:
- Thus, when the resistance R is decreased, the power dissipated in the resistor increases.
Final Answer:
The power dissipated in the resistor will increase when the resistance is decreased.
---
- We have a resistor R connected to an ideal battery. An ideal battery provides a constant voltage (or EMF) E with no internal resistance.
- The power P dissipated in a resistor can be calculated using the formula:
P=V2R
- Here, V is the voltage across the resistor, which is equal to the EMF E of the battery.
- Initially, the power dissipated in the resistor R is:
P=E2R
- Now, if we decrease the resistance R to a new value R′ (where R′<R), the voltage across the resistor remains the same (still equal to E).
- The new power P′ dissipated in the resistor R′ is:
P′=E2R′
- Since R′<R, it follows that:
E2R′>E2R
- This implies that:
P′>P
- Therefore, the power dissipated in the resistor increases when the resistance is decreased.
- Thus, when the resistance R is decreased, the power dissipated in the resistor increases.
The power dissipated in the resistor will increase when the resistance is decreased.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Taking it together
142 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - B. Assertion and reason
18 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Example
65 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective
11 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrances gallery
25 Videos
Similar Questions
A resistor of resistance R is connected to a cell internal resistance 5Ω. The value of R is varied from 1Ω to 5Ω. The power consumed by R
View SolutionTwo resistors A and B of resistance 4 Ω and 6 Ω respectively are connected in parallel. The combination is connected across a 6 volt battery of negligible resistance. Calculate :
the power dissipated in each resistor.
View SolutionThree resistors having resistances of 1.60Ω,2.40Ω and 4.80Ω are connected in parallel to a 28.0V battery that has negligible internal resistance. Find
(a) the equivalent resistance of the combination.
(b) the current in each resistor.
(c) the total current through the battery.
(d) the voltage across each resistor.
(e) the power dissipated in each resistor.
(f) which resistor dissipates the maximum power the one with the greatest resistance or the least resistance? Explain why this should be.
View SolutionStatement I: When an external resistor of resistance R (connected across a cell to internal resistance r ) is varied, power consumed by resistance R is maximum when R = r.
Statement II: Power consumed by a resistor of constant resistance R is maximum when current through it is maximum.
View SolutionA 50 mH inductor is in series with a 10 ohm resistor and a battery with an emf of 25 V. At t = 0 the switch is closed. Find
the power dissipated in the resistor
View SolutionFour equal resistance dissipated 5 W of power together when connected in series to a battery of negligible internal resistance . The total power dissipated in these resistance when connected in parallel across the same battery would be .
View SolutionWhat will be the motion of the conductor of the previous problem, if a resistor of resistance R is connected into the circuit instead of the capacitor? Neglect the resistance of the conductors.
View Solutionin the figure shown , a circuit contains two identical resistors with resistance R=Ω and an inductance with L=2 H ,An ideal battery of 15 V is connected in the circuit what will be the current through the battery long after the switch is clossed ?
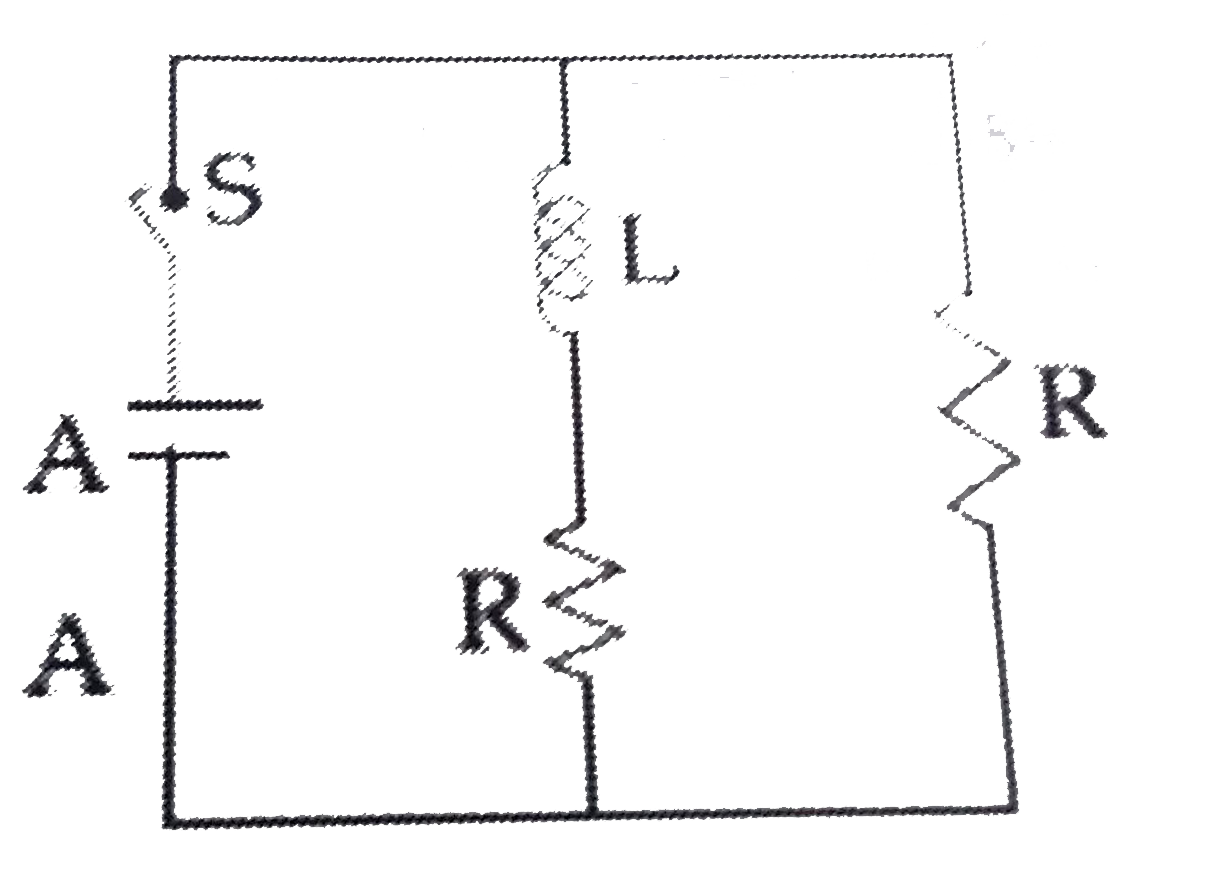
View SolutionFigure shows three resistor configurations R1,R2 and R3 connected to 3 V battery .

If the powers dissipated by the configuration R1,R2 and R3 are P1,P2 and P3, respectively, then
View SolutionFigure shows three resistor configurations R1,R2 and R3 connected to 3 V battery .

If the powers dissipated by the configuration R1,R2 and R3 are P1,P2 and P3, respectively, then
View Solution
