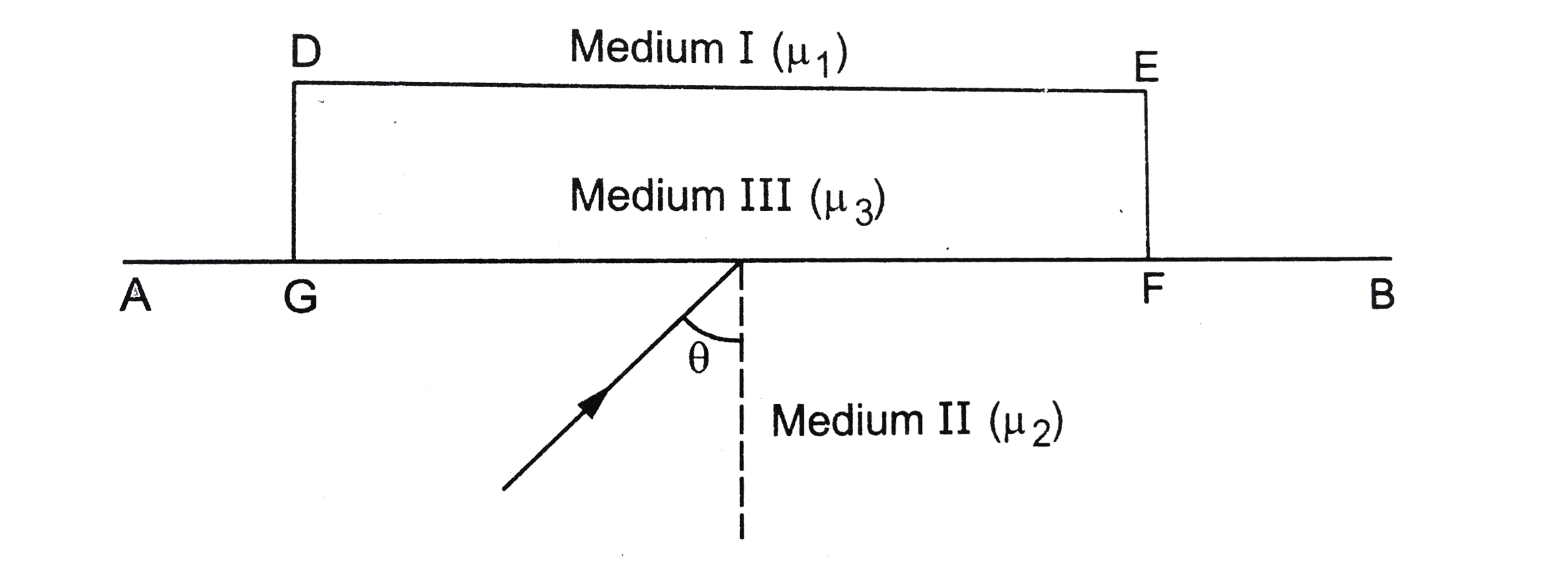
Monochromatic light is incident on plane interference AB between two media of refractive indices μ1 and μ2(μ2>μ1) at angle of incidence θ as shown in the figure.
The angle θ is infinitesimally greater than the critical angle for the two media so that total internal reflection takes places. Now if a transparent slab DEFG of uniform thickness and of refractive index μ3 is introduced on the interface (as shown in the figure), show that for any value of μ3 all light will ultimately be reflected back again into medium II. Consider separately the cases.
(a) μ3<μ1 , (b) μ3>μ1
We will use the symbol ≤ to mean 'infinitesimally greater than'.
When the slab is not inserted,
θ≤θc=sin−1(μ1/μ2) or sinθ≥μ1/μ2
When the slab is inserted, we have two cases
μ3≤μ1 and μ3>μ1.
Case I. μ3<μ1 . We have sinθ≥μ1/μ2≥μ3/μ2
Thus, the light is incident on AB at an angle greater than the critical angle sin−1(μ3/μ2). It suffers total internal reflection and goes back to medium II.
Case II. μ3>μ1
sinθ≥μ1/μ2<μ3/μ2
Thus, the angle of incidence θ may be smaller than the critical angle sin−1(μ3/μ2) and hence it may enter medium III. The angle of refraction θ is given by (figure).
sinθsinθ′=μ3μ2 (i)
⇒sinθ′=μ2μ3sinθ≤μ2μ3⋅μ1μ2
Thus, sinθ′≥μ1μ3⇒θ′≥sin−1(μ1μ3) (ii)
As the slab has parallel faces, the angle of refraction at the face FG is equal to the angle of incidence at the face DE. Equation (ii) shows that this angle is infinitesimally greater than the critical angle here. Hence, the light suffers total internal reflection and falls at the surface FG at an angle of incidence θ′. At this face, it will refract into medium II and teh angle or refraction will be θ as shown by Eq. (i). Thus, the total ligh energy is ultimately reflected back into medium II.

Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Solved Examples
15 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Exercise1.1
14 Videos
- ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.3
15 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit
27 Videos
Similar Questions
Monochramatic light is incident on the pLane interface AB between two media of refractive indices μ1 and μ2(μ2>μ1) at an angle of incidence theta as shown in figure. The angle theta is infinitesimally greater thannte critical angle for the two media so thast total internal reflection takes place. Now, if a transparent slab DEFG of uniform thickness and of refractive inde μ2 is introduced on theinterface (as shown in figure ) , show that for any value of μ2 all light will ultimately be reflected back into medium II.
View SolutionWhat is the relation between the refractive indicesμ,μ1 and μ2 if the behaviour of light rays is shown in Figure.
View Solution
A ray is incident on interface of two media at critical angle as shown in the figure.
View SolutionFor total internal reflection to take place, the angle of incidence i and the refractive index μ of the medium must satisfy the inequality
View SolutionA light ray is incident on a glass sphere of reflective index μ=√3 at an angle of incidence 60∘ as shown in Fig. Find the angles r, r′ e and the total deviation after two refractions.
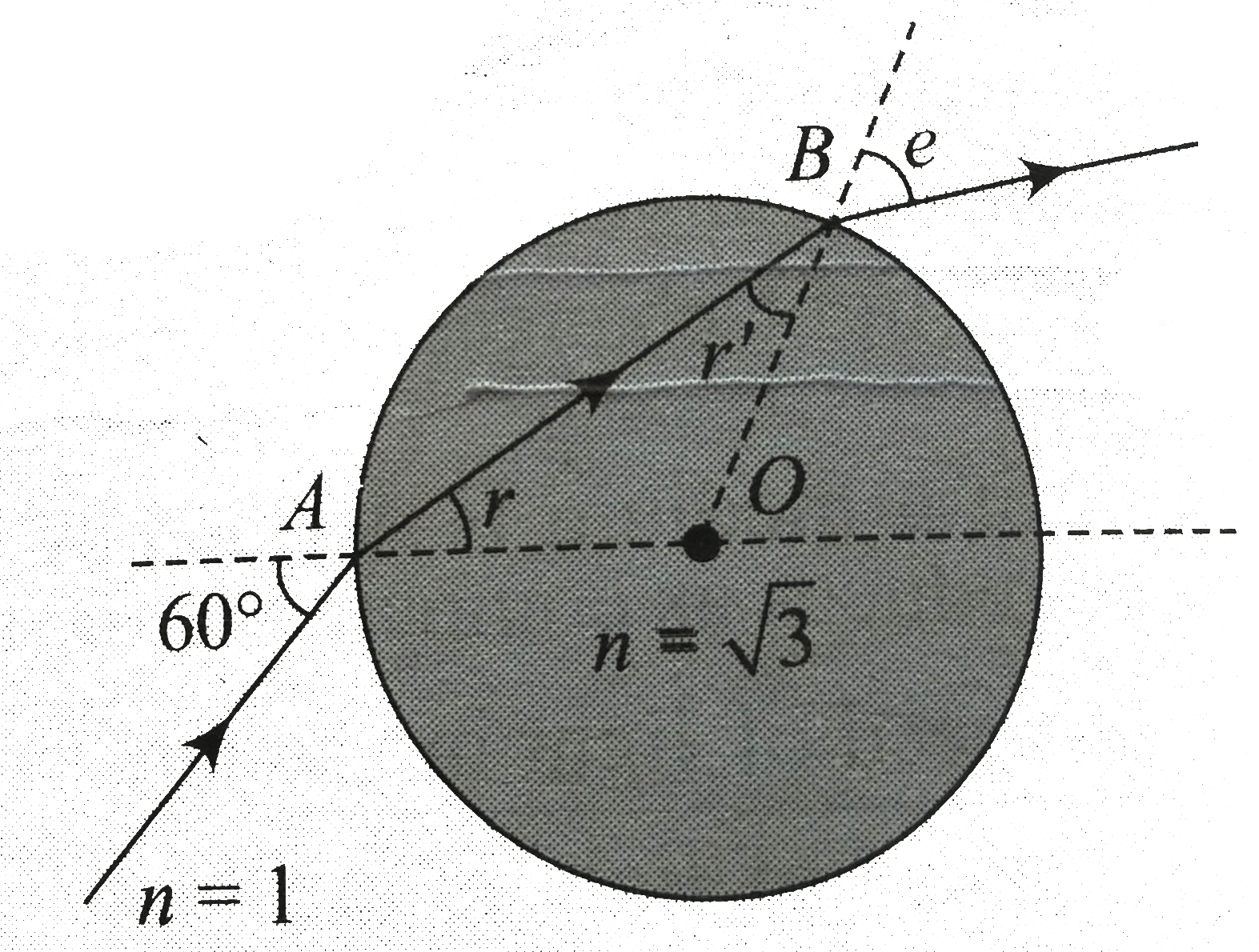
View SolutionUnder what conditions is the phenomenon of total internal reflection between the critical angle of incidence and the refractive index of the medium.
View SolutionWhen a monochromatic light ray is incident on a medium of refracive indexμwith angle of incidence θ1,the angle of refraction is θr.if θi is changed slightly byΔθi,then the corresponding change in θrwill be-
View SolutionThe diagram shows a spherical surface which separates two media of refractive index, μ1andμ2. Respectively. Now, a point object is placed on the principal axis as shown in the figure. Then
View SolutionA ray of light is incident on the left vertical face of glass cube of refractive index n2, as shown in figure. The plane of incidence is the plane of the page, and the cube is surrounded by liquid (refractive index=n1). What is the largest angle of incidence θ1 for which total internal reflection occurs at the top surfaces?

View SolutionLight ray is incident on a prism of angle A=60∘ are refractive index μ=√2. The angle of incidence which the emergent rays grazes the surface is given
View Solution
