In question 118, if m1 and m2 are the magnifications for two positions of the lens, then
f=dm1+m2
f=2dm1+m2
f=3dm1−m2
f=dm1−m2
The correct Answer is:d.
To solve the problem, we need to establish the relationship between the focal length of a lens and the magnifications (m1 and m2) for two different positions of the lens. Here’s a step-by-step breakdown of the solution:
Step 1: Understand the Setup
We have a lens that can be moved between two positions while still forming an image on the same screen. The distance from the object to the lens in the first position is d1 and in the second position is d2. The distance between the lens positions is d, and the total distance from the object to the screen is D.
Step 2: Use the Lens Formula
The focal length f of the lens can be related to the distances using the lens formula:
1f=1d1+1d2
Step 3: Define the Magnifications
The magnifications for the two positions of the lens are given by:
m1=hiho=D+dD−d
m2=hiho=D−dD+d
Step 4: Find the Difference in Magnifications
To find the relationship between the magnifications, we calculate m1−m2:
m1−m2=D+dD−d−D−dD+d
Step 5: Simplify the Expression
To simplify m1−m2, we find a common denominator:
m1−m2=(D+d)2−(D−d)2(D−d)(D+d)
Expanding the numerator:
(D+d)2−(D−d)2=D2+2Dd+d2−(D2−2Dd+d2)=4Dd
Thus, we have:
m1−m2=4Dd(D−d)(D+d)
Step 6: Relate to Focal Length
From the lens formula, we can also express the focal length as:
f=D2−d24D
Now, substituting D2−d2 in terms of f:
D2−d2=4fD
Thus, we can relate D and d to f:
m1−m2=4Dd4fD=df
Step 7: Final Relationship
Rearranging gives us:
f=dm1−m2
Conclusion
The relationship between the focal length f and the magnifications m1 and m2 is:
f=dm1−m2
We have a lens that can be moved between two positions while still forming an image on the same screen. The distance from the object to the lens in the first position is d1 and in the second position is d2. The distance between the lens positions is d, and the total distance from the object to the screen is D.
The focal length f of the lens can be related to the distances using the lens formula:
1f=1d1+1d2
The magnifications for the two positions of the lens are given by:
m1=hiho=D+dD−d
m2=hiho=D−dD+d
To find the relationship between the magnifications, we calculate m1−m2:
m1−m2=D+dD−d−D−dD+d
To simplify m1−m2, we find a common denominator:
m1−m2=(D+d)2−(D−d)2(D−d)(D+d)
Expanding the numerator:
(D+d)2−(D−d)2=D2+2Dd+d2−(D2−2Dd+d2)=4Dd
Thus, we have:
m1−m2=4Dd(D−d)(D+d)
From the lens formula, we can also express the focal length as:
f=D2−d24D
Now, substituting D2−d2 in terms of f:
D2−d2=4fD
Thus, we can relate D and d to f:
m1−m2=4Dd4fD=df
Rearranging gives us:
f=dm1−m2
The relationship between the focal length f and the magnifications m1 and m2 is:
f=dm1−m2
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Assertion-Reasoninig
2 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Linked Comprehension
51 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Subjective
26 Videos
- ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.3
15 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit
27 Videos
Similar Questions
Assertion: In displacement method of finding focal length of a convex lens its magnification in one position of lens is +2, then magnification in another position of lens should be −12.
Reason:This method can't be applied for a concave lens.
View SolutionAn object and a screen are fixed at a distance d apart. When a lens of focal length f is moved between the object and the screen, sharp images of the object are formed on the screen for two positions of the lens.
The magnifications produced at these two positions are M1andM2-
View SolutionIn Figure, find the total magnification after two successive reflections first ono M1 and then on M2.
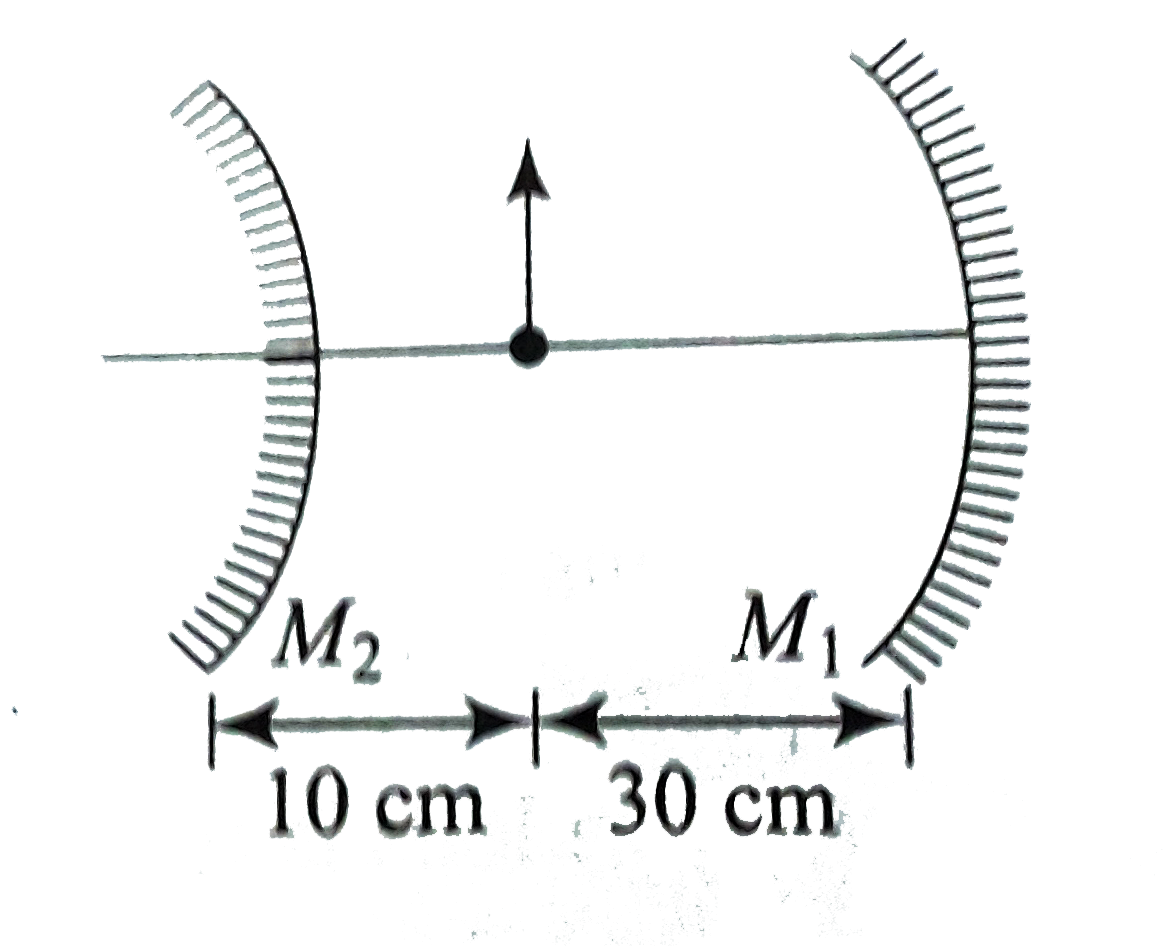
View SolutionIn Figure, find the total magnification after two successive reflections first ono M1 and then on M2.

View SolutionTwo bodies of masses m1 and m2 are placed distant d apart. Show that the position where the gravitational field due to them is zero, the potential is given by, V=−Gd(m1+m2+2√m1m2)
View SolutionAn equi-convex lens of focal length F in air is is cut into two halves along the plane perpendicular to the optic axis. One of the halves is placed between a fixed object and a screen separated by distance of 90 cm . Two images are formed on the screen for two different positions of the lens with magnification 2 and 1/2 respectively. Find the value of F . what would be the value of the focal length of the equiconvex lens if the lens is immersed in water ? Refractive index of the material of the lens is 1.5 and that of water is μw=4/3.
View SolutionA convex lens of focal length f is placed somewhere in between an object and a screen. The distance between the object and the screen is x. If the numerical value of the magnification produced by the lens is m, then the focal lnegth oof the lens is .
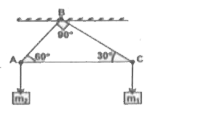
View SolutionTwo masses m1 and m2 are hanging from the two corners of a triangular frame of wire as shown in the adjacent figure. The arm AC of the triangular frame is horizontal. The ratio of m1 and m2 is
View SolutionA bomb at rest explodes into two parts of masses m1 and m2. If the momentums of the two parts be P1 and P2, then their kinetic energies will be in the ratio of:
View SolutionThe lateral magnification of the lens with an object located at two different position u1 and u2 are m1 and m2 , respectively. Then the focal length of the lens is
View Solution
