Assertion: In displacement method of finding focal length of a convex lens its magnification in one position of lens is +2, then magnification in another position of lens should be −12.
Reason:This method can't be applied for a concave lens.
If both Assertion and Reason are true and the Reason is correct explanation of the Assertion.
If both Assertion and Reason are true but Reason is not the correct explanation of the Assertion.
If both Assertion is true, but the Reason is false.
If both Assertion is false but the Reason is true.
The correct Answer is:B
To solve the question, we need to analyze both the assertion and the reason provided.
1. Understanding the Assertion:
- The assertion states that in the displacement method of finding the focal length of a convex lens, if the magnification in one position of the lens is +2, then the magnification in another position of the lens should be -1/2.
- In the displacement method, the relationship between the magnifications (m1 and m2) at two different positions of the lens is given by the equation:
m1×m2=−1
- If we let m1=+2, we can find m2:
2×m2=−1⟹m2=−12
- Thus, the assertion is true.
2. Understanding the Reason:
- The reason states that the displacement method cannot be applied to a concave lens.
- This is true because the displacement method relies on the fact that the magnification can be positive or negative depending on the position of the object and the image. For a concave lens, the image formed is always virtual and upright, leading to a positive magnification. Therefore, the relationship m1×m2=−1 cannot be satisfied for a concave lens.
- Hence, the reason is also true.
3. Conclusion:
- Both the assertion and the reason are true.
- However, the reason does not correctly explain the assertion, as the assertion is specifically about the magnification relationship for a convex lens.
Final Answer:
- Both the assertion and the reason are true, but the reason is not the correct explanation for the assertion.
---
- The assertion states that in the displacement method of finding the focal length of a convex lens, if the magnification in one position of the lens is +2, then the magnification in another position of the lens should be -1/2.
- In the displacement method, the relationship between the magnifications (m1 and m2) at two different positions of the lens is given by the equation:
m1×m2=−1
- If we let m1=+2, we can find m2:
2×m2=−1⟹m2=−12
- Thus, the assertion is true.
- The reason states that the displacement method cannot be applied to a concave lens.
- This is true because the displacement method relies on the fact that the magnification can be positive or negative depending on the position of the object and the image. For a concave lens, the image formed is always virtual and upright, leading to a positive magnification. Therefore, the relationship m1×m2=−1 cannot be satisfied for a concave lens.
- Hence, the reason is also true.
- Both the assertion and the reason are true.
- However, the reason does not correctly explain the assertion, as the assertion is specifically about the magnification relationship for a convex lens.
- Both the assertion and the reason are true, but the reason is not the correct explanation for the assertion.
Topper's Solved these Questions
- REFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFRACTION OF LIGHTEXERCISE - Level 1 Objective
38 Videos
- REFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFRACTION OF LIGHTEXERCISE - Objective Questions
1 Videos
- REFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFRACTION OF LIGHTEXERCISE - Exercise 31.8
8 Videos
- REFLECTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFLECTION OF LIGHTEXERCISE - Subjective
9 Videos
- SEMICONDUCTORSBOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORSEXERCISE - Subjective
12 Videos
Similar Questions
Calculate focal length of given lens if the magnification is −0.5.
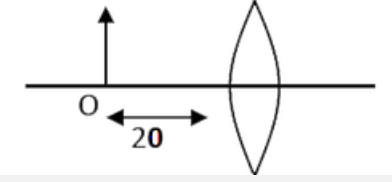
View SolutionFocal length of concave lens shown in figure is 60 cm. Find image position and its magnification.

View SolutionIn displacement method distance of object from convex lens of focal length 20 cm in one position 60 cm. Then
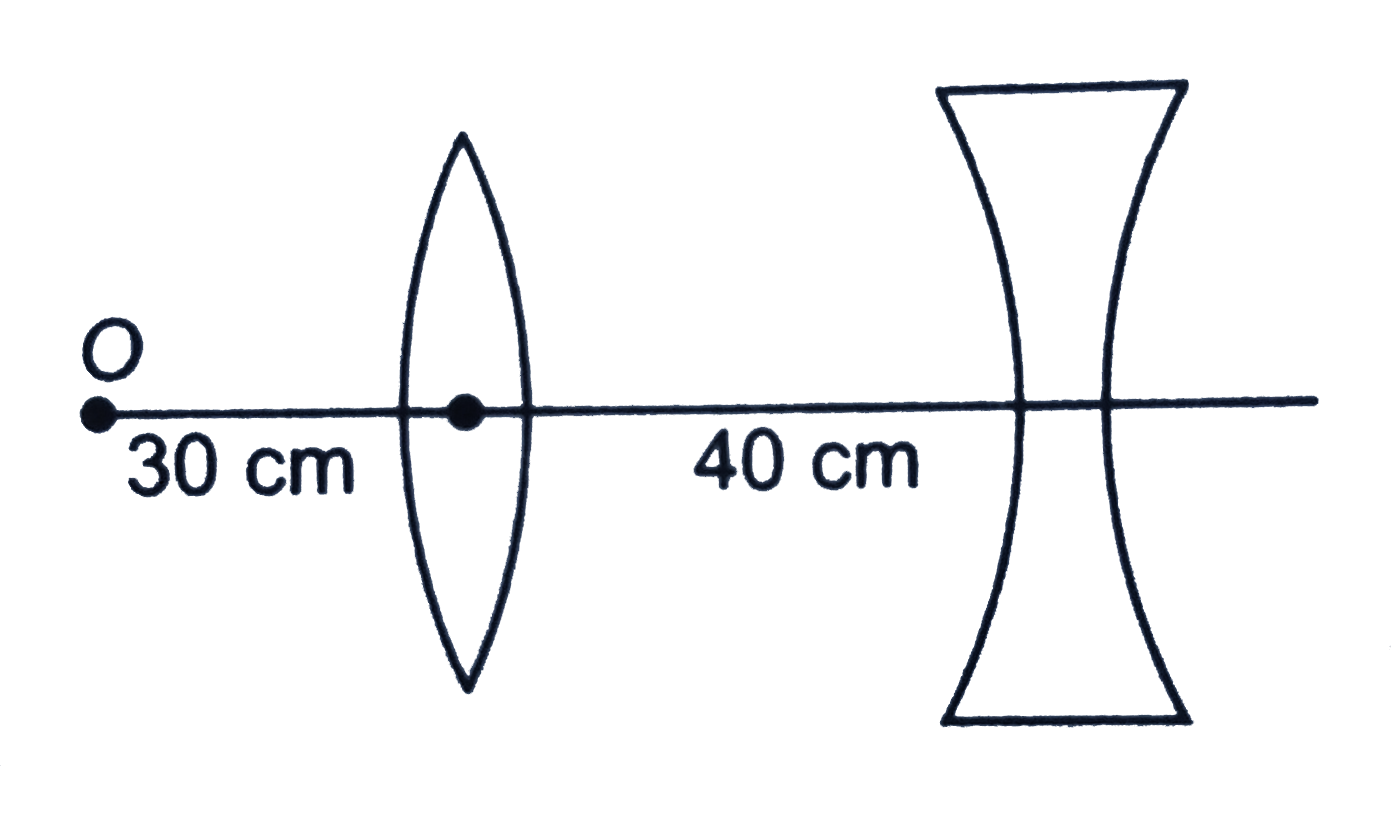
View SolutionFocal length of a convex lense in air is 20cm. and of concave lens 40cm. Find the position of final image.
View SolutionIn question 118, if m1 and m2 are the magnifications for two positions of the lens, then
View SolutionThe focal length of a converging lens is 8 cm. Fins the magnification power when it is used as a reading lens to form the image at near point.
View SolutionIn the displacement method , a convex lens is placed in between an object and a screen . If one of them magnification is 3 and the displacement of the lens between the two positions is 24 cm , then the focal length of the lens is :-
View SolutionIn a displacement method the distance between the object and the screen is 70 cm and the focal length of the lens is 16 cm, find the separations of the magnified and diminished image position of the lens.
View SolutionDistance of an object from a concave lens of focal length 20 cm is 40 cm. Then linear magnification of the image
View SolutionAn object is placed at a distance of 12 cm from a convex lens of focal length 8 cm. Find :
the position of the image
View Solution
