The convex surface of a thin concave-convex lens of glass of refractive index 1.5 has a radius of curvature 20 cm. The concave surface has a radius of curvature 60 cm. The convex side is silvered and placed on a horizontal surface as shown in figure. (a) Where should a pin be placed on the axis so that its image is formed at the same place ? (b) If the concave part is filled with water (mu = 4/3), find the distance through which the pin should be moved so that the image of the pin again coincides with the pin.

x=5cm
x=20cm
x=15cm
x=25cm
The correct Answer is:C
Method 1: The optical arrangement is equivalent to the concave mirror of focal length F given by
1F=1fg+1fm+1fg
where fx is th efocal length of the lens without silvering and fm is the focal length of the mirror.
1fg=(n−1)(1R1−1R2)
=(1.5−1)(120−1+60)=160
fg=60cm
fg=R1/2=20/2=10cm
1F=160+110+160=860
F=608=7.5cm
For the image to be formed at the place of the object,
X=R=2F=7.5×2
=15cm
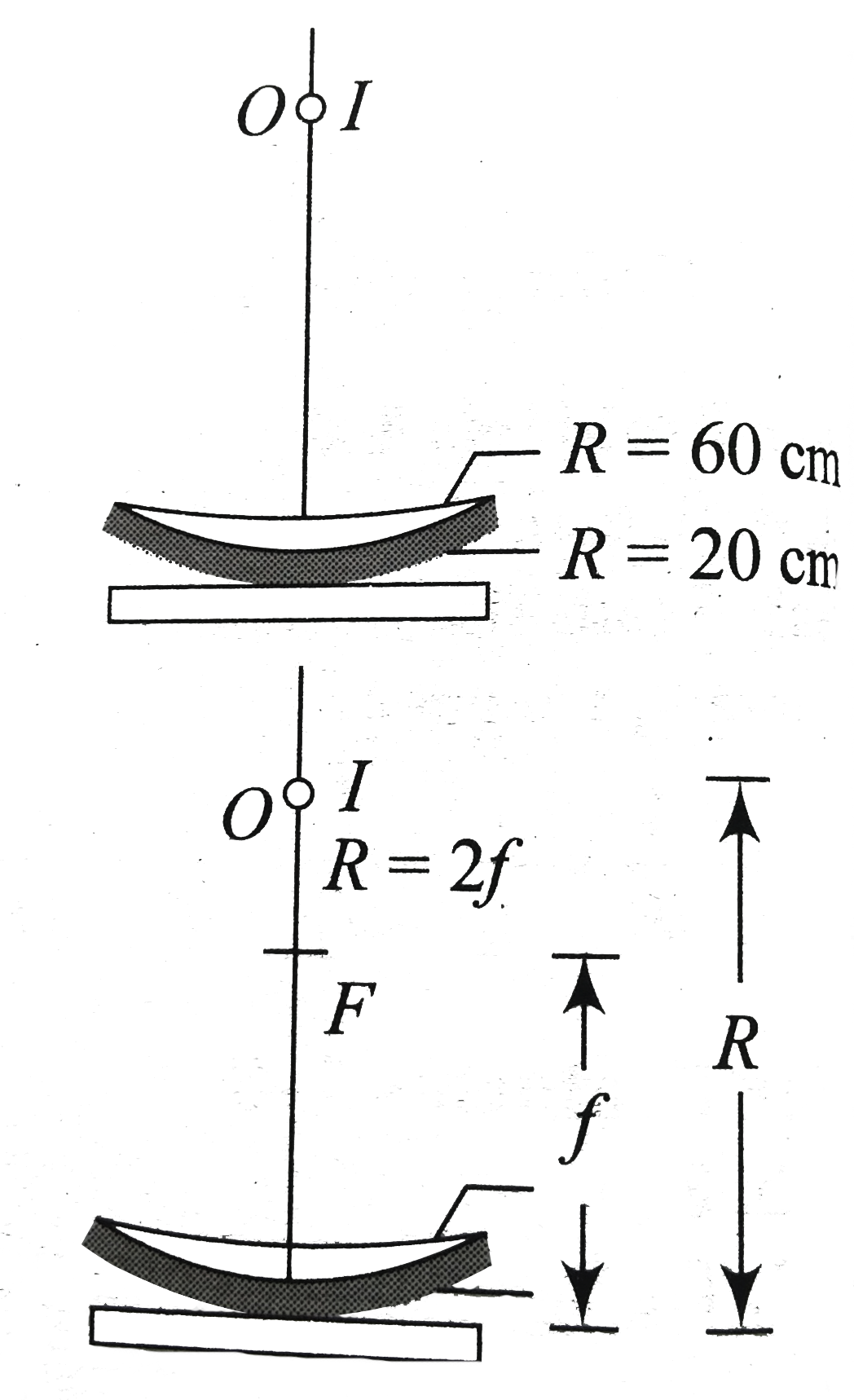
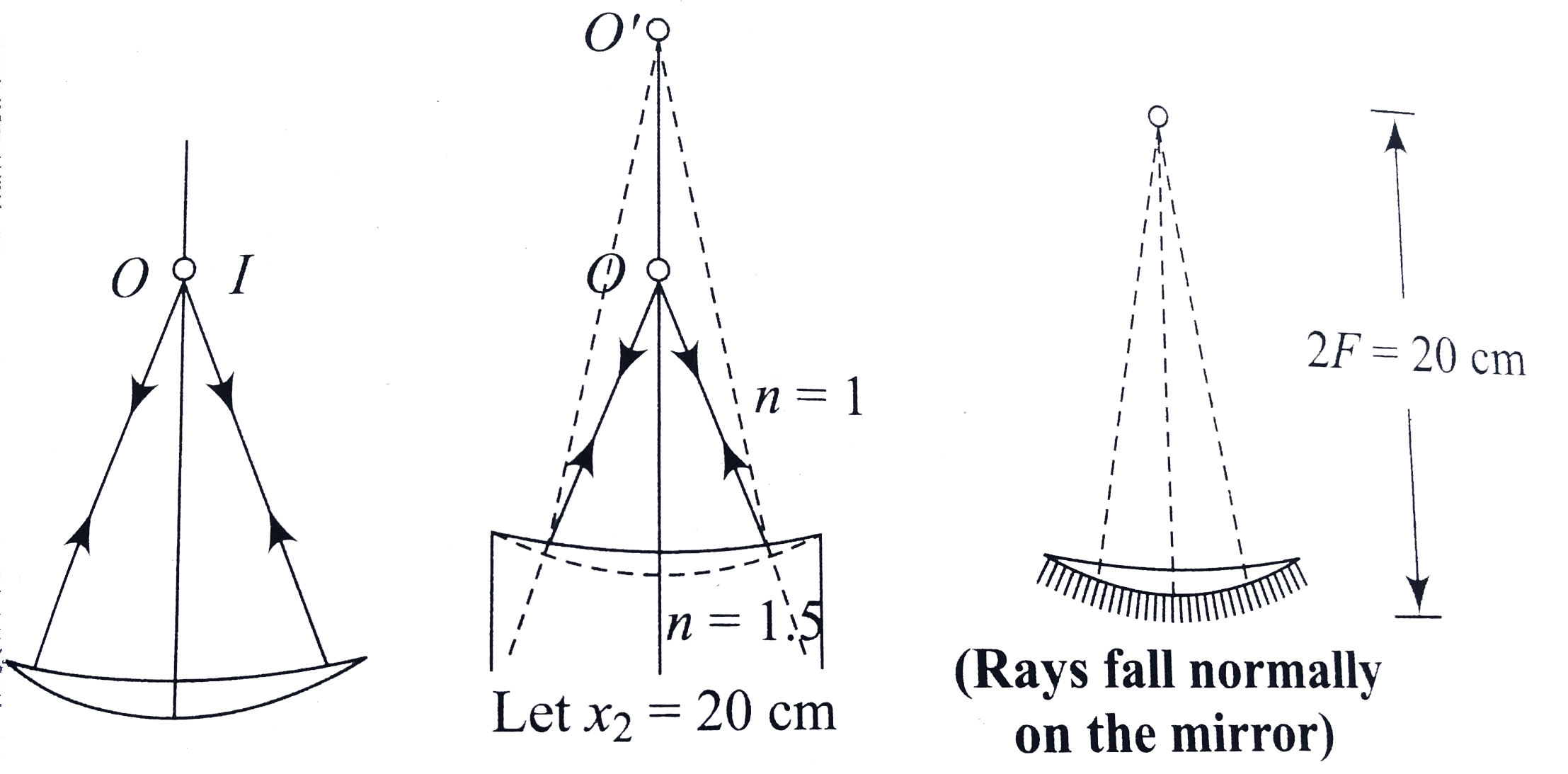
Method2: We use the relation
n2x2−n1x1=n2−n1R
For the object and the image to coincide, the rays fall normal on the reflecting surface. i.e., on the silvered face of the lens.
Then, the rays retrace backward and meet at the object point again (optical reversibility).
For the refraction at the upper surface of the lens,
n1=1.0,n2=1.5,x1=20,R=+60
(x2=+20 ensures that the rays fall on the silvered face normally. )
1.520−1.0x1=1.5−1.0+60
1.0x1=1.520−0.560=3.060
x1=15cm
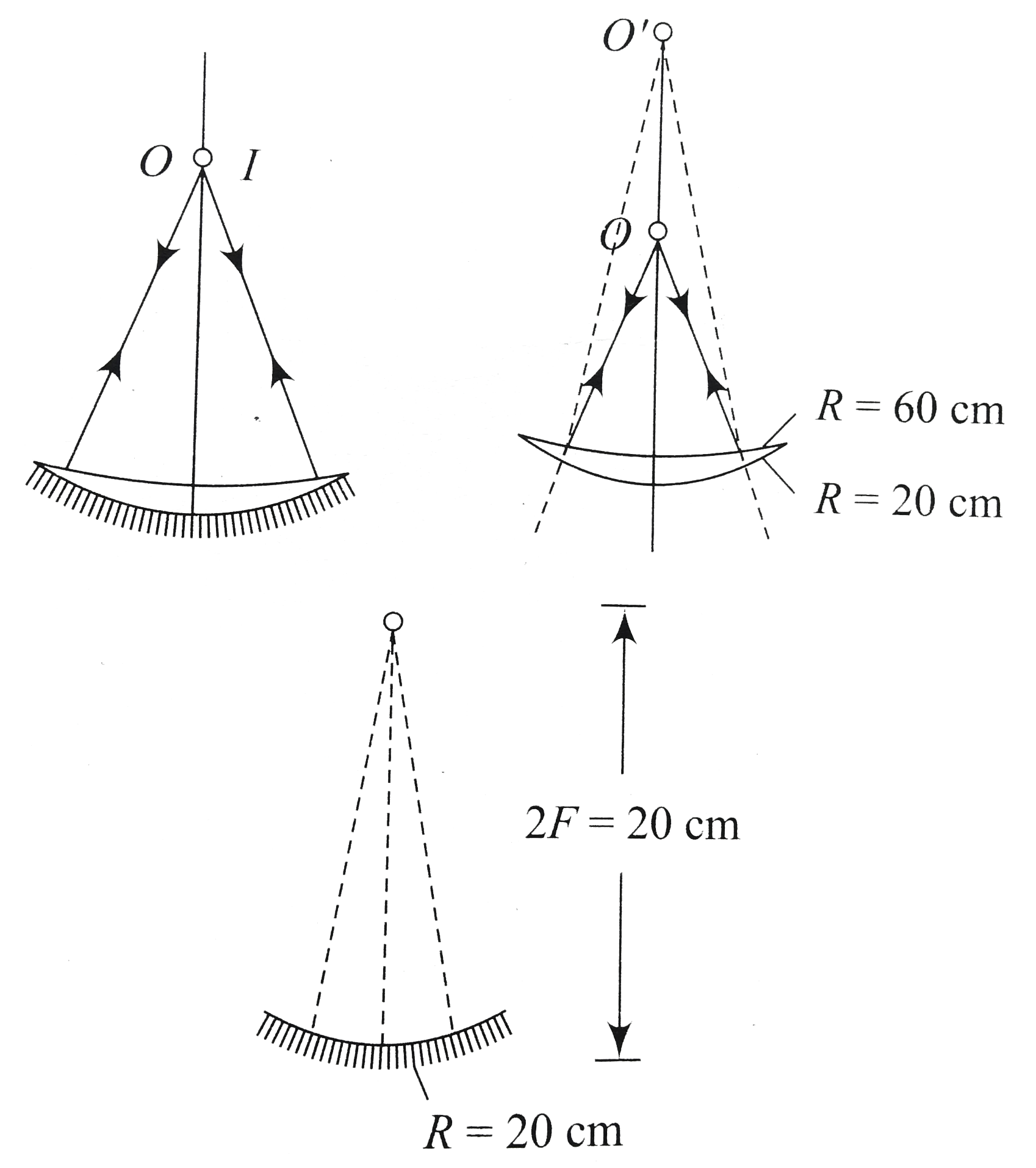
Method 3: We use lensmaker's formula and the equation
1f=1x2−1x1
The given optical arrangement can be visualised as a convex lens of focal length 60cm and a concave mirror of focal length 10cm kept in contact as shown in the figure.
If the rays fall normally on the mirror after the refraction through the lens, they will retrace backward and meet at the point of the pin again.
For the lens, x1=?
x2=+20 (for normal incidence on the mirror )
f=−60 (using cartesian-coordinate sign convention)
1−60=1+20−1x1
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Integer15videos
GEOMETRICAL OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Archives7videos
GEOMETRICAL OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Assertion-Reasoninig2videos
GEOMETRICAL OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.315videos
ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit27videos
HEATING EFFECT OF CURRENT
Similar Questions
Knowledge Check
- Question 1 - Select One
A double convex lens is made of glass of refractive index 1.55 with both faces of same radius of curvature. Find the radius of curvature required, if focal length is 20cm.
A11cmB22cmC7cmD6cm - Question 2 - Select One
The radius curvature of each surface of a convex lens of refractive index 1.5 is 40 cm. Calculate its power.
A2.5DB2DC1.5DD1D
The convex side of a thin concavo-convex lens of glass of refractive index 1.5 has a radius of curvature of 20cm. The concave surface has a radius of curvature of 60cm. What is the focal length of the lens? The convex side is silvered and placed on a horizontal surface. What is the effective focal length of the silvered lens? The concave part is filled with water with refractive index 1.33. What is the effective focal length of the combined glass and water lens? If the convex side is silvered what is the new effective focal length of the silvered compound lens?
View SolutionThe concave and convex surface of a thin concavo-convex lens of refractive index 1.5 has radius of curvature 50 cm and 10 cm respectively. The concave side is slivered then if the equivalent focal length of the silvered lends is −5xcm then find x.
View SolutionA double convex lens is made of glass of refractive index 1.55 with both faces of same radius of curvature. Find the radius of curvature required, if focal length is 20cm.
View SolutionA double convex lens is made of glass of refractive index 1.55 with both faces of same radius of curvature. Find the radius of curvature required, if focal length is 20cm.
View SolutionA concavo-convex lens is made of glass of refractive index 1.5. The radii of curvature of its two surfaces are 30cm and 50cm. Its focal length when placed in a liquid of refractive index 1.4 is
View SolutionThe plane surface of a plano-convex lens of refracting index 1.5, is silvered. The radius of curvature of curved surface is R. Find the focal length of the mirror thus formed.
View Solution

