Two parallel beams of light P and Q are incident normally on a prism and the transmitted rays are brought to focus with the help of a convergent lens as shown in Fig. 2.23. If the intensities of the upper and lower beams immediately after transmission from face AC are 4I abd I, respectively, find the resultant intensity at the focus.
To solve the problem, we need to find the resultant intensity at the focus after two beams of light with different intensities pass through a prism and are focused by a lens. Let's break down the solution step by step.
Step 1: Identify the intensities of the beams
The problem states that the intensities of the upper and lower beams immediately after transmission from face AC are:
- Intensity of beam P (upper beam), I1=4I
- Intensity of beam Q (lower beam), I2=I
Step 2: Use the formula for resultant intensity
The resultant intensity IR when two coherent light beams interfere is given by the formula:
IR=I1+I2+2√I1I2cosϕ
where ϕ is the phase difference between the two beams.
Step 3: Substitute the values of I1 and I2
Substituting the values of I1 and I2 into the formula:
IR=4I+I+2√(4I)(I)cosϕ
IR=5I+2√4I2cosϕ
IR=5I+4Icosϕ
Step 4: Simplify the expression
The resultant intensity can be simplified as:
IR=5I+4Icosϕ
Step 5: Determine the phase difference ϕ
To find the phase difference ϕ, we need to consider the path difference between the two beams. In this case, if the beams are transmitted through the prism and focused, we can assume that the path difference is negligible, leading to ϕ=0.
Step 6: Substitute ϕ=0 into the intensity equation
Substituting ϕ=0:
IR=5I+4Icos(0)
IR=5I+4I⋅1
IR=5I+4I=9I
Final Result
The resultant intensity at the focus is:
9I
---
The problem states that the intensities of the upper and lower beams immediately after transmission from face AC are:
- Intensity of beam P (upper beam), I1=4I
- Intensity of beam Q (lower beam), I2=I
The resultant intensity IR when two coherent light beams interfere is given by the formula:
IR=I1+I2+2√I1I2cosϕ
where ϕ is the phase difference between the two beams.
Substituting the values of I1 and I2 into the formula:
IR=4I+I+2√(4I)(I)cosϕ
IR=5I+2√4I2cosϕ
IR=5I+4Icosϕ
The resultant intensity can be simplified as:
IR=5I+4Icosϕ
To find the phase difference ϕ, we need to consider the path difference between the two beams. In this case, if the beams are transmitted through the prism and focused, we can assume that the path difference is negligible, leading to ϕ=0.
Substituting ϕ=0:
IR=5I+4Icos(0)
IR=5I+4I⋅1
IR=5I+4I=9I
The resultant intensity at the focus is:
9I
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Solved Examples10videos
WAVE OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Exercise 2.112videos
WAVE OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - single correct Ansewer type12videos
SOURCES OF MAGNETIC FIELD
Similar Questions
_E01_102_Q01.png)
In a YDSE a parallel beam of light of wavelength 6000Å is incident on slits at angle of incidence 30∘. A and B are two thin transparent films each of refractive index 1.5. thickness of A is 20.4μm. Light coming through A and B have intensities I and 4I resepctively on the screen. Intensity at point O which is symmetric relative to the slits is 3I. The central maxima is above O.
(i). what is the maximum thickness of B to do so.
Assuming thickness of B to be that found in part (i)
Answer the following parts.
(ii). Find fringe width, maximum intensity and minimum intensity on screen.
(iii). Distance of nearest minima from O
(iv) intensity at 5 cm on either side of O.View SolutionTwo parallel wires P and Q placed at a separation d =6 cm on x-axis carry electric current i1=5Aandi2=2A in opposite directions as shown in Fig. Find the point on the line PQ where the resultant mgnetic field is zero.
 View Solution
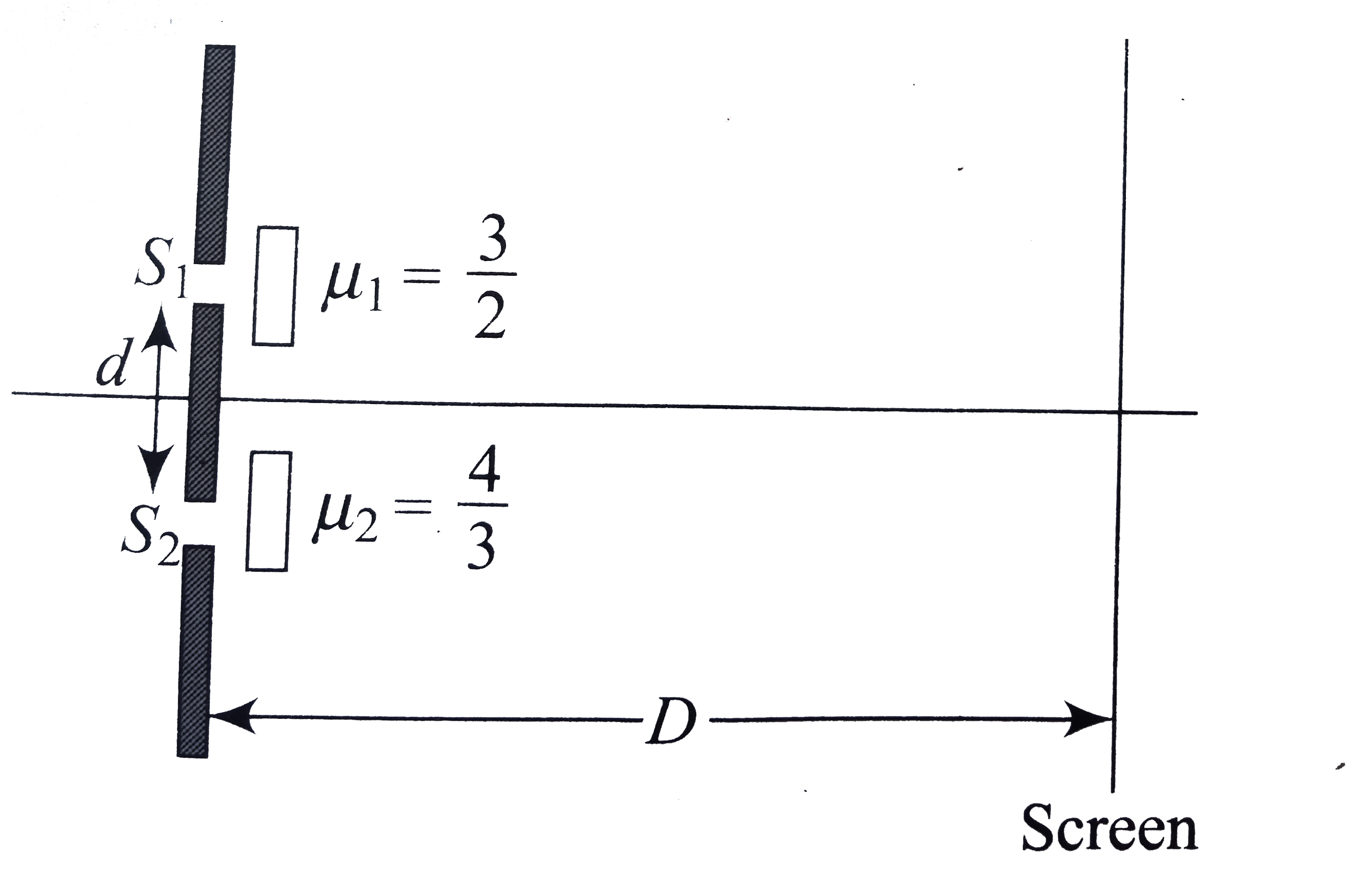
View SolutionIn the figure an arrangement of young's double slit experiment is shown. A parallel beam of light of wavelength 'λ' (in medium n1) is incident at an angle 'θ' as shown. Distance S1O=S2O. Point 'O' is the origin of the coordinate system. The medium on the left and right side of the plane of slits has refractive index n1 and n2 respectively. Distance between the slits is d. The distance between the screen and the plane of slits is D.
Using D=1m,d=1mm,θ=30∘,λ=0.3mm,n1=43,n2=109, answer the following

If the intensity due to each light wave at point 'O' is I0 then the resultant intensity at point 'O' will be -View SolutionIn the figure an arrangement of young's double slit experiment is shown. A parallel beam of light of wavelength 'λ' (in medium n1) is incident at an angle 'θ' as shown. Distance S1O=S2O. Point 'O' is the origin of the coordinate system. The medium on the left and right side of the plane of slits has refractive index n1 and n2 respectively. Distance between the slits is d. The distance between the screen and the plane of slits is D.
Using D=1m,d=1mm,θ=30∘,λ=0.3mm,n1=43,n2=109, answer the following

If the intensity due to each light wave at point 'O' is I0 then the resultant intensity at point 'O' will be -View SolutionTwo monochromatic ray of light are incident normally on the face AB of an isosceles right - angled 'I' and '2' are respectively 1.35 and 1.45. Trace path of these rays after entering through the prism.
 View Solution
View SolutionA monochromatic beam of light of 6000 Å is used in YDSE set-up. The two slits are covered with two thin films of equal thickness t but of different refractive indices as shown in figure. Considering the intensity of the incident beam on the slits to be I0, find the point on the screen at which intensity is I0 and is just above the central maxima. (Assume that there is no change in intensity of the light after passing through the films.) Consider t=6μm,d=1mm, and D=1m, where d and D have their usual meaning. Give your answer in mm.
 View Solution
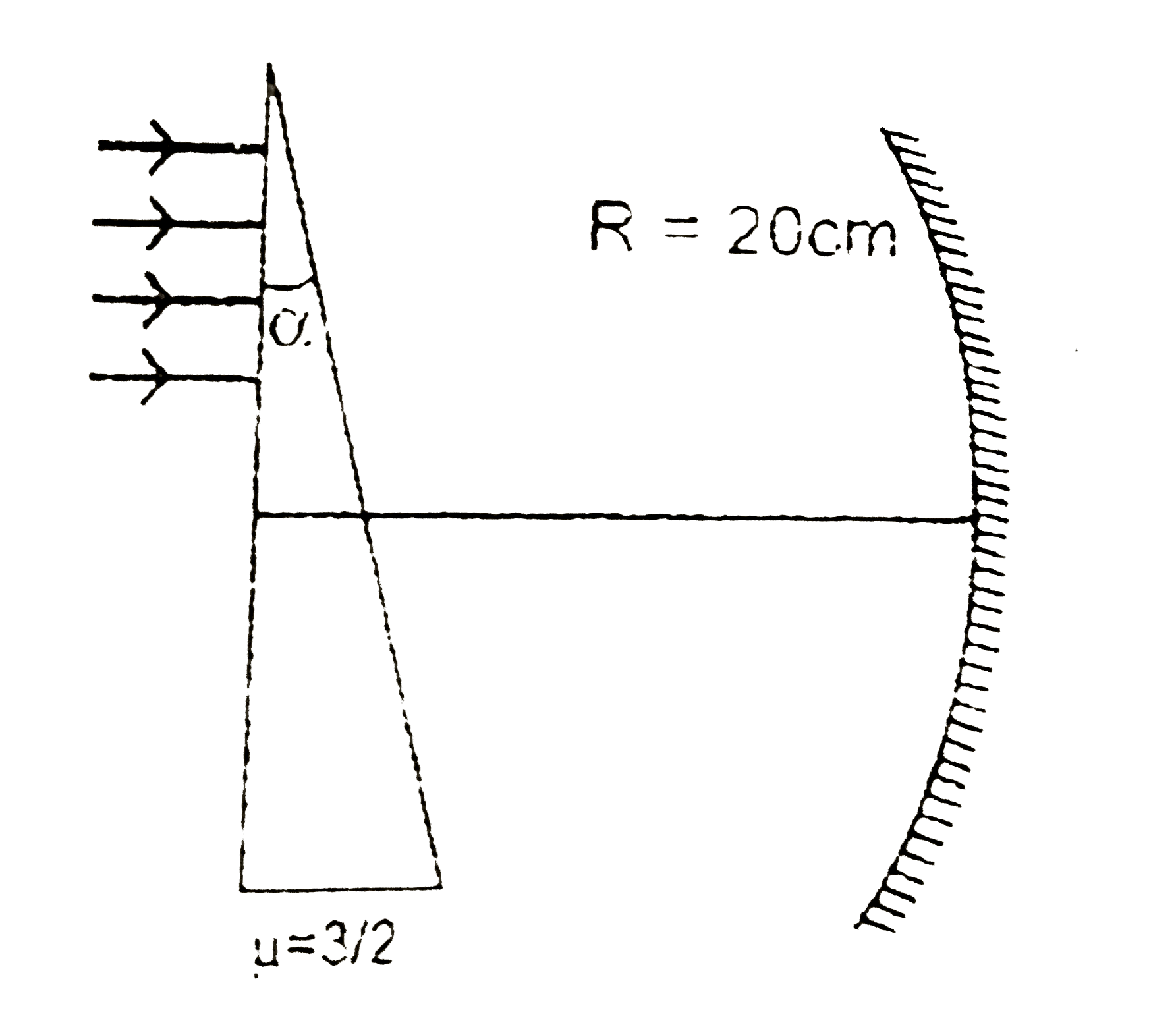
View SolutionIn the given figure a parallel beam of ligth is incident on the upper part of a prism of angle 1.8∘ and R.I.3/2 . The light coming out of the prism falls on a concave mirror of radius of curvature 20cm. The distance of the point (where the rays are focused after reflrction from the mirror) from the pricipal axis is: [use π=3.14]
 View Solution
View SolutionA coherent parallel beam of microwaves of wavelength λ=0.5mm falls on aYoung's double- slit apparatus. The separation between the slits is 1.0 mm. The intensity of microwaves is measured on a screen placed parallel to the plane of the slits at a distance of 1.0 m from it as shown in Fig. 2.42.
If the incident beam makes an angle or 30∘ with the x-axis (as in the dotted arrow shown in the figure), find the y-coordinates of the first minima on either side of the central maximum.
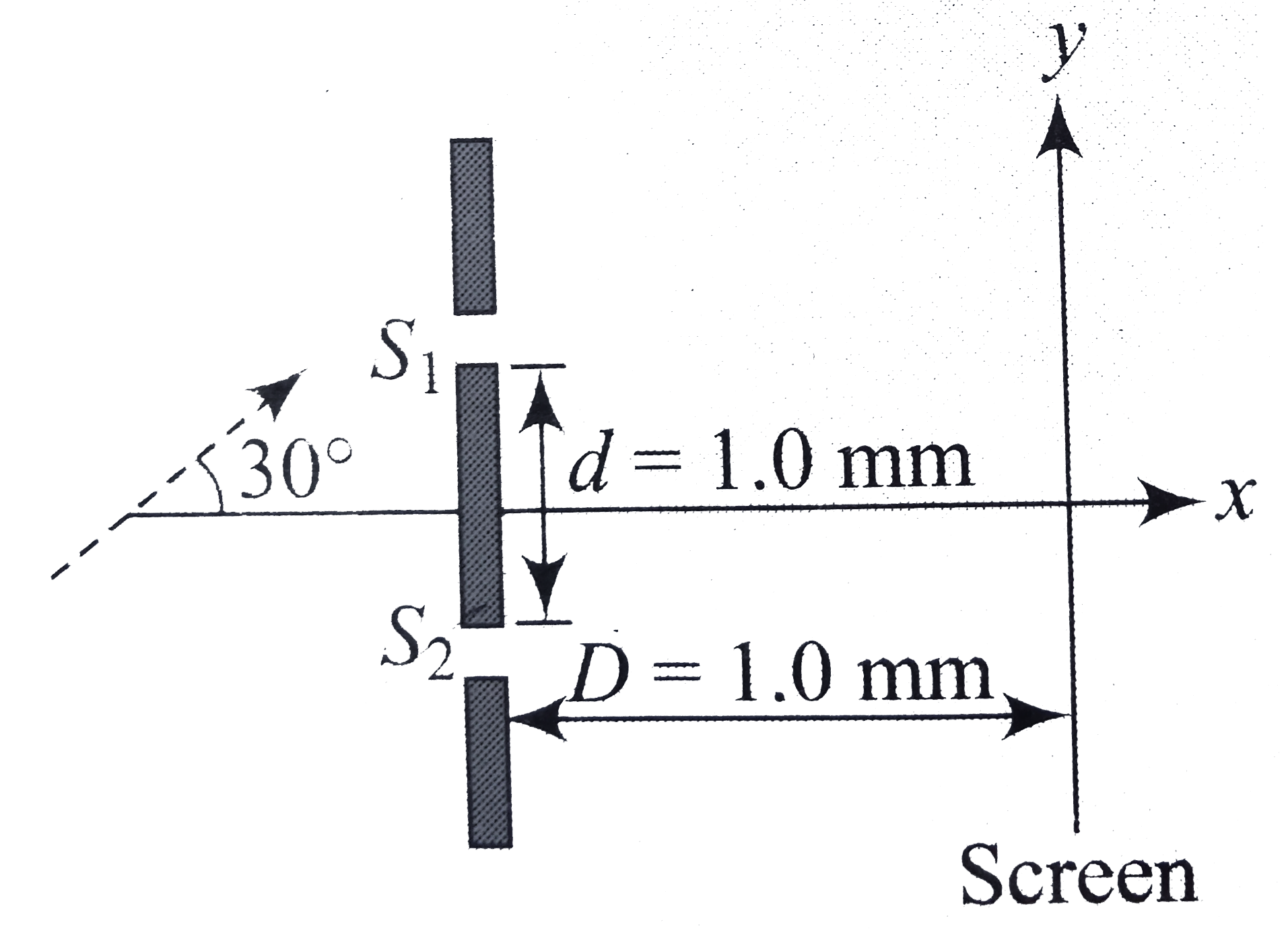 View Solution
View SolutionL is a lens such that a parallel beam of light I ncident on it, after refraction, converges to a point at a distance x from it and M is a mirror such that a parallel lbeam of light incident on it, after reflection, converges to a point at a distance y from it. Now the lens L and mirror M are placed at a distan 2(x+y) from each other. An object of size 2 cm is kept infront of lens at a distance 2x from it. Find the nature, position , and size of the image that willl be seen by an observer looking toward the mirror through the lens.
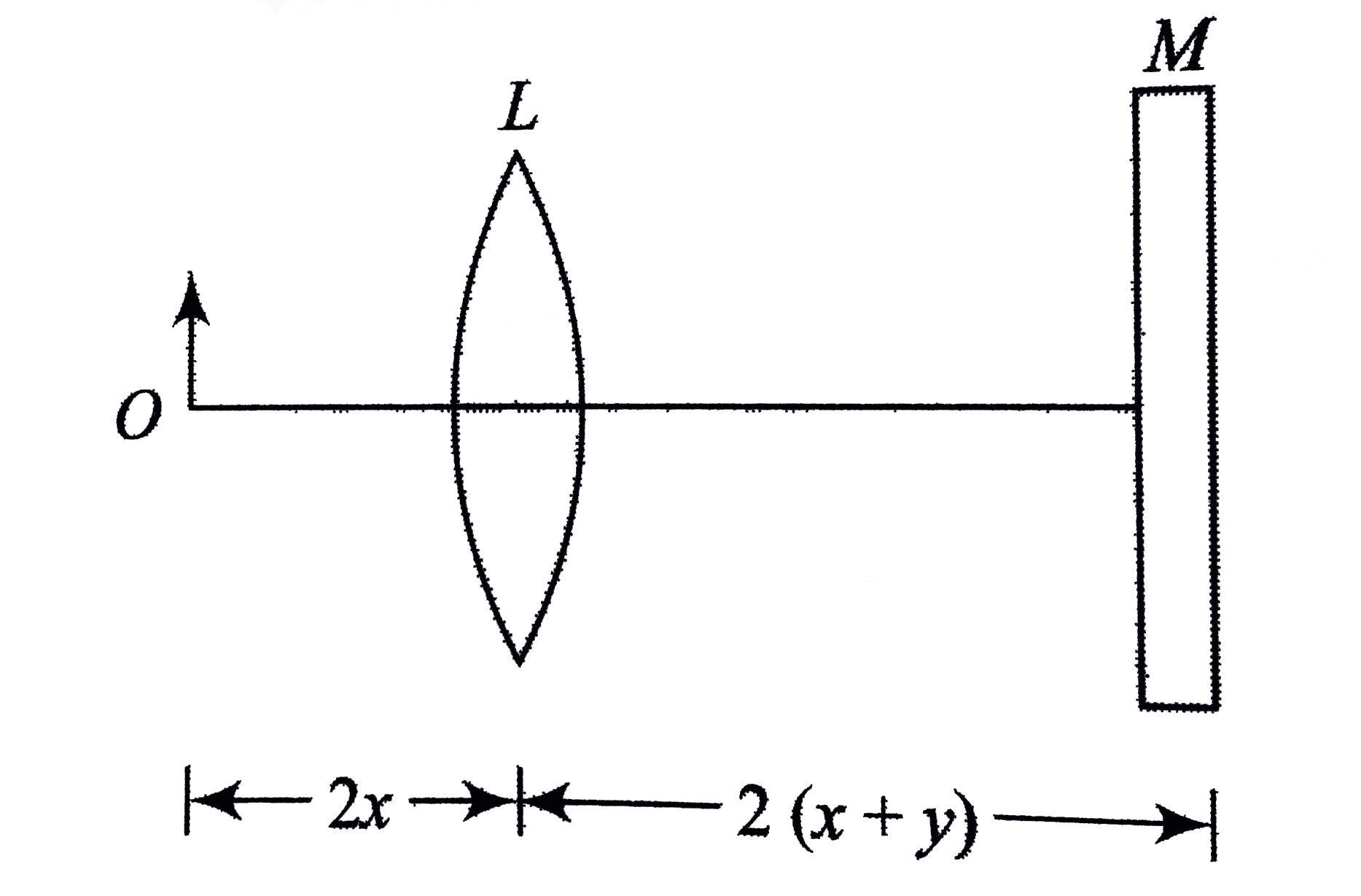 View Solution
View SolutionA parallel beam of light (λ=5000Å) is incident at an angle θ=30∘ with the normal to the slit plane in a Young's double slit experiment. The intensity due to each slit is I0. Point O is equidistant from S1andS2. The distance between slits is 1mm.
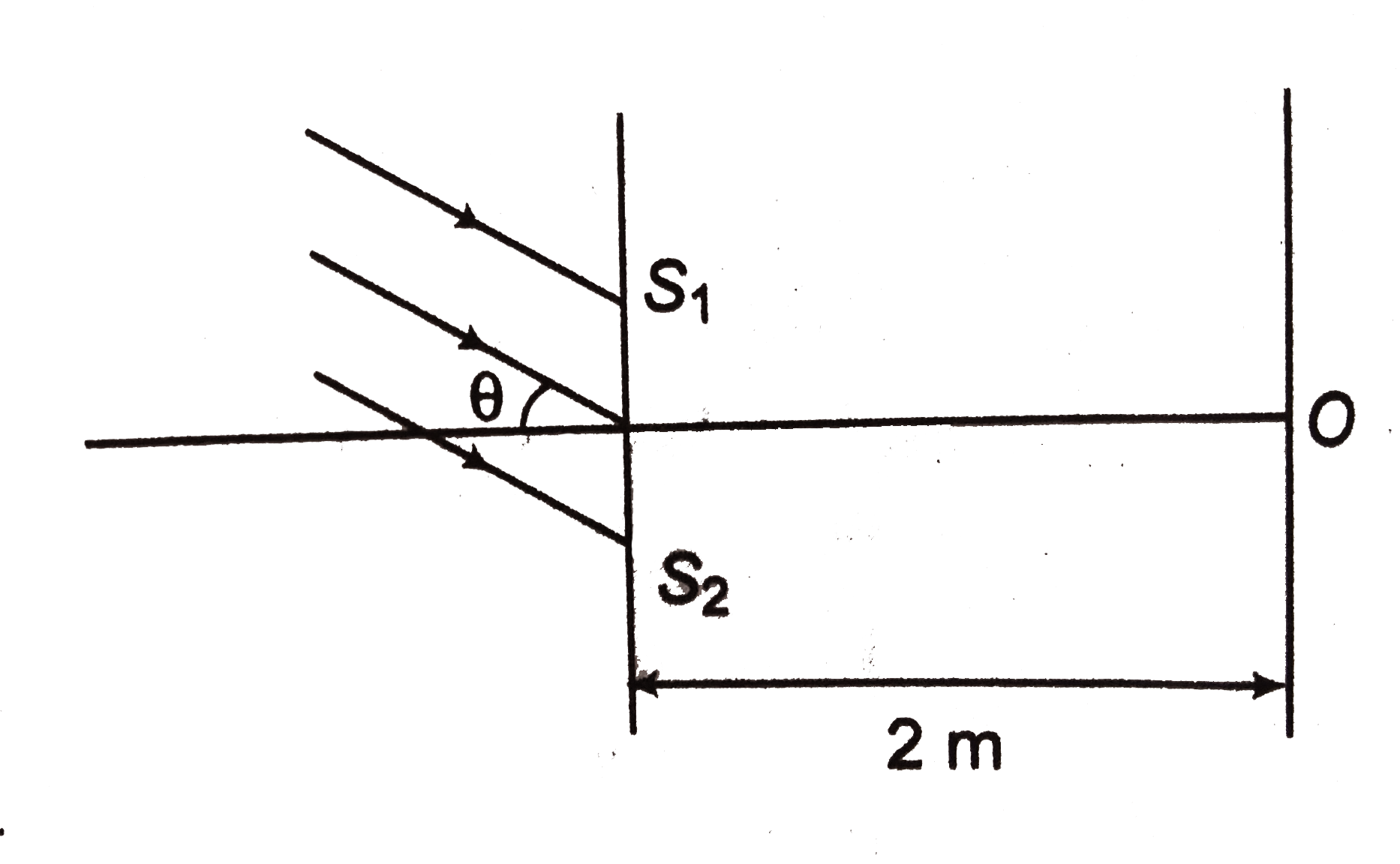 View Solution
View Solution

