A partical of mass M at rest decays into two Particles of masses
m1andm2 having non-zero velocities. The ratio of the de - Broglie wavelengths
of the particles λ1∣λ2 is
(a) m1/m2 (b)m2/m1 (c ) 1 (d)√2/√1
m2m1
m1m2
√m1√m2
1:1
The correct Answer is:D
λ=hmv
Here, 0×M=m1v1+m2v2
Clearly, m1v1=−m2v2
In magnitude,
mv = constant
λ1λ2=11
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PHOTOELECTRIC EFFECTEXERCISE - Multiple Correct10videos
PHOTOELECTRIC EFFECT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PHOTOELECTRIC EFFECTEXERCISE - Linked Comprehension44videos
PHOTOELECTRIC EFFECT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PHOTOELECTRIC EFFECTEXERCISE - Subjective16videos
PHOTOELECTRIC EFFECT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NUCLEAR PHYSICSEXERCISE - ddp.5.514videos
NUCLEAR PHYSICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RAY OPTICSEXERCISE - DPP 1.612videos
RAY OPTICS
Similar Questions
A praticle of mass M at rest decays into two particle of masses m1 and m2, having non-zero velocities. The ratio of the de Broglie wavelength of the particles λ1λ2 is
View SolutionA particle of mass 3m at rest decays into two particles of masses m and 2m having non-zero velocities. The ratio of the de Broglie wavelengths of the particles (λ1λ2) is
View Solution
Knowledge Check
- Question 1 - Select One
A particle of mass 4m at rest decays into two particles of masses m and 3m having non-zero velocities. The ratio of the de Broglie wavelengths of the particles 1 and 2 is
A12B14C2D1 - Question 2 - Select One
The reduce mass of two particles having masses m and 2 m is
A2 mB3 mC2 m/3Dm/2 - Question 3 - Select One
Two particles A1andA2 of masses m1,m2(m1>m2) have the same de-broglie wavelength. Then
Atheir momenta are the same.Btheir energies are the same.Cmomentum of A1 is less than the momentum of A2.Denergy of A1 is more than the energy of A2.
Two bodies of masses m1andm2(<m1) are connected to the ends of a massless cord and allowed to move as shown in figure. The pulley is both massless and frictionless. The acceleration of the centre of mass is (m1−m2)n(m1+m2)2g. Find the value of n.
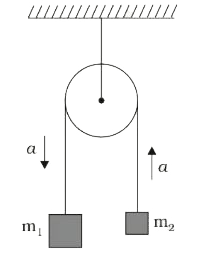 View Solution
View SolutionAssertion: A particle of mass M at rest decays into two particles of masses m1 and m2, having non-zero velocities will have ratio of the de-broglie wavelength unity.
Reason: Here we cannot apply conservation of linear momentum.View SolutionTwo particles of masses m and 2m have equal kinetic energies. Their de Broglie wavelengths area in the ratio of:
View SolutionThe de-Broglie wavelength of a particle with mass 1g and velocity 100m/sec is.
View SolutionTwo particles A1andA2 of masses m1,m2(m1>m2) have the same de-broglie wavelength. Then
View Solution

