The disintegration rate of a certain radioactive sample at any instant is 4750 disintegrations per minute. Five minutes later the rate becomes 2700 per minute. Calculate
(a) decay constant and (b) half-life of the sample
We have,
N=N0e−λt
The activity of the sample is given by
dNdt=−λN0e−λt=−λN
i.e., activity is proportional to be the number of undercyed nuclei.
At t0,(dNdt)t=0=−λn
At t=5min,((dN).(dt))t=5minm=−λN
∴N0N=(dNdt)t=0(dNdt)t=5min=47502700=1.760
a. From Eg. (i), we have
NN0=e−λt
or N0N=eλtor loge(N0)N=λt
⇒λ=1tloge(N0)N=2.3026t×log10(N0N)
Substituting give values, we have
λ=2.30265×0.2455=0.113−1min
b. Half-life of sample , T=0.6931λ=0.69310.113=6.1−1min.
Topper's Solved these Questions
- NUCLEAR PHYSICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NUCLEAR PHYSICSEXERCISE - Exercise 5.1
10 Videos
- NUCLEAR PHYSICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NUCLEAR PHYSICSEXERCISE - Exercise 5.2
27 Videos
- NUCLEAR PHYSICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NUCLEAR PHYSICSEXERCISE - ddp.5.5
14 Videos
- MISCELLANEOUS VOLUME 5BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Integer
12 Videos
- PHOTOELECTRIC EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PHOTOELECTRIC EFFECTEXERCISE - Integer Type
4 Videos
Similar Questions
A counter rate metre is used to measure the activity of a radioactive sample. At a certain instant, the count rate was recorded as 400 counters per minute. Five minutes later, the count recorded was 200 counts per min. Calculate the decay and half-period of the sample.
View SolutionA radioactive sample at any instant has its disintegration rate 5000 disintegrations per minute After 5 minutes , the rate is 1250 disintegration per minute. Then , the decay constant (per minute)
View Solution
Knowledge Check
Half Life of a certain radioactive substance is 69.3 days. Its disintegration constant is:
A0.010day−1B0.100day−1C0.001day−1D1.00day−1
Half life of a certain radioactive element is 3-465 days. Find its disintegration constant.
View SolutionA radioactive element has rate of disintegration 10,000 disintegrations per minute at a particular instant. After four minutes it becomes 2500 disintegrations per minute. The decay constant per minute is
View SolutionA certain radioactive substance has a half-life period of 30 days. What is the disintegration constant ?
View SolutionThe variation of decay rate of two radioactive samples A and B with time is shown in fig.
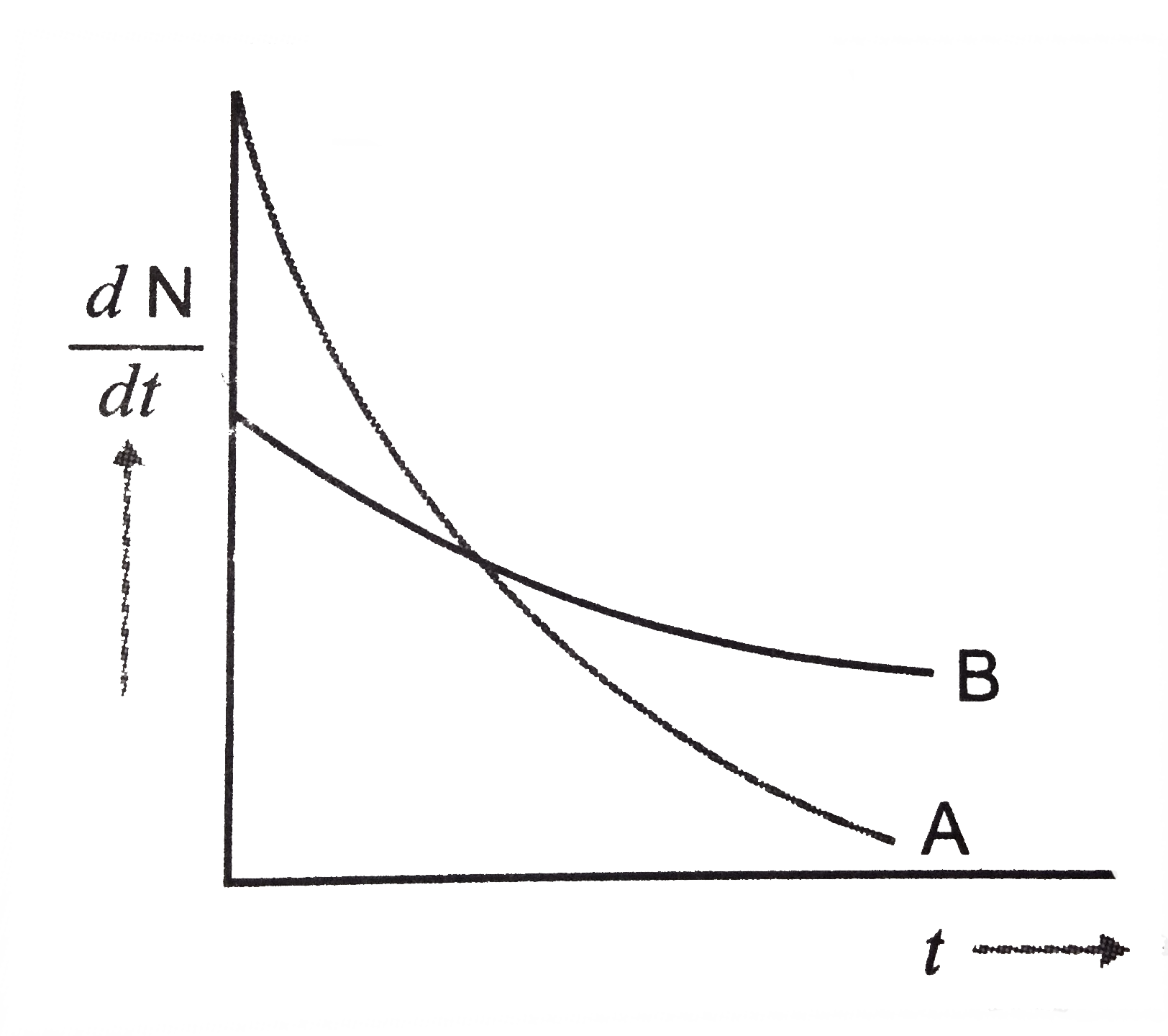
Which of the following statements are true?
View SolutionThe variation of decay rate of two radioactive samples A and B with time is shown in fig.

Which of the following statements are true?
View SolutionThe activity of a radioactive sample is measured as 9750 counts per minute at t=0 and as 975 counts per minute at t=5 minutes. The decay constant is approximately
View SolutionA free neutron has half life of 14 minutes. Its decay constant is
View Solution
