Two parallel horizontal conductors are suspended by two light vertical threads each 75 cm long. Each conductor has a mass of 40gm−1, and when there is no current they are 0.5 cm apart. Equal current in the two wires result in a separation of 1.5 cm. Find the values and directions of currents. Take g=9.8ms−2.
To solve the problem step by step, we will analyze the forces acting on the conductors and apply the relevant formulas.
Step 1: Understand the setup
We have two parallel conductors suspended by threads. Each conductor has a mass of 40 g/m, and when no current flows, they are 0.5 cm apart. When equal currents flow through them, they repel each other and the separation increases to 1.5 cm.
Step 2: Identify forces acting on the conductors
1. Gravitational Force (Weight): The weight of each conductor can be calculated using:
W=mg
where m=40g/m=0.04kg/m (mass per unit length) and g=9.8m/s2.
2. Tension in the threads: The tension T in the threads has two components:
- Vertical component Tcosθ=mg
- Horizontal component Tsinθ=F (the magnetic force)
Step 3: Calculate the weight of each conductor
The weight per unit length of the conductor is:
W=0.04kg/m×9.8m/s2=0.392N/m
Step 4: Use the magnetic force formula
The magnetic force between two parallel conductors carrying current I is given by:
F=μ0I2L2πd
where:
- μ0=4π×10−7T m/A (permeability of free space)
- L is the length of the conductors
- d is the distance between the conductors
Step 5: Set up the equations
From the tension components:
1. Tcosθ=mg
2. Tsinθ=F
Using small angle approximation, tanθ≈sinθ:
sinθcosθ=Fmg
Thus,
tanθ≈FW
Step 6: Calculate the angles
The initial separation is d1=0.5cm=0.005m and the final separation is d2=1.5cm=0.015m.
Step 7: Substitute values into the equations
Using the final separation:
F=4π×10−7I2L2π(0.015)=2×10−7I2L0.015
Step 8: Relate forces to weight
From the earlier equations:
2×10−7I2L0.015=0.3920.75
This simplifies to:
I2=0.392×0.015×0.752×10−7L
Step 9: Solve for I
Assuming L=1m:
I2=0.392×0.015×0.752×10−7=0.0004395
I=√0.0004395≈0.021A≈21mA
Step 10: Determine the direction of the current
Since the conductors repel each other, the currents must be in opposite directions.
Final Answer
The current in each conductor is approximately 21mA and the currents are in opposite directions.
We have two parallel conductors suspended by threads. Each conductor has a mass of 40 g/m, and when no current flows, they are 0.5 cm apart. When equal currents flow through them, they repel each other and the separation increases to 1.5 cm.
1. Gravitational Force (Weight): The weight of each conductor can be calculated using:
W=mg
where m=40g/m=0.04kg/m (mass per unit length) and g=9.8m/s2.
- Vertical component Tcosθ=mg
- Horizontal component Tsinθ=F (the magnetic force)
The weight per unit length of the conductor is:
W=0.04kg/m×9.8m/s2=0.392N/m
The magnetic force between two parallel conductors carrying current I is given by:
F=μ0I2L2πd
where:
- μ0=4π×10−7T m/A (permeability of free space)
- L is the length of the conductors
- d is the distance between the conductors
From the tension components:
1. Tcosθ=mg
2. Tsinθ=F
sinθcosθ=Fmg
Thus,
tanθ≈FW
The initial separation is d1=0.5cm=0.005m and the final separation is d2=1.5cm=0.015m.
Using the final separation:
F=4π×10−7I2L2π(0.015)=2×10−7I2L0.015
From the earlier equations:
2×10−7I2L0.015=0.3920.75
This simplifies to:
I2=0.392×0.015×0.752×10−7L
Assuming L=1m:
I2=0.392×0.015×0.752×10−7=0.0004395
I=√0.0004395≈0.021A≈21mA
Since the conductors repel each other, the currents must be in opposite directions.
The current in each conductor is approximately 21mA and the currents are in opposite directions.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Solved Example20videos
SOURCES OF MAGNETIC FIELD
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Concept Exercise 2.135videos
SOURCES OF MAGNETIC FIELD
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RAY OPTICSEXERCISE - DPP 1.612videos
RAY OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Comprehension Type14videos
WAVE OPTICS
Similar Questions
Two points objects of mass 1.5g and 2.5g respectively are a distance of 16cm apart, the center of mass is at distance x from the object of mass 1.5g. Find the value of x
View SolutionThe long, staight wires, each carrying an electric current of 5.0 A, are kept parallel to each other at a separation of 2.5 cm. Find the magnitude of the magnetic force experienced by 10 cm of a wire.
View Solution
Knowledge Check
- Question 1 - Select One
Two long and parallel straight wires A and B are carrying currents of 4A and 7A in the same directions are separated by a distance of 5cm. The force acting on a 8cm section of wire A is
A3×10−6NB6×10−6NC9×10−6ND12×10−6N
The force between two parallel conductor, each of length 50m and distance 20 cm apart, is 10−2N. If the current in one conductor is double that in another one, then their values will respectively be
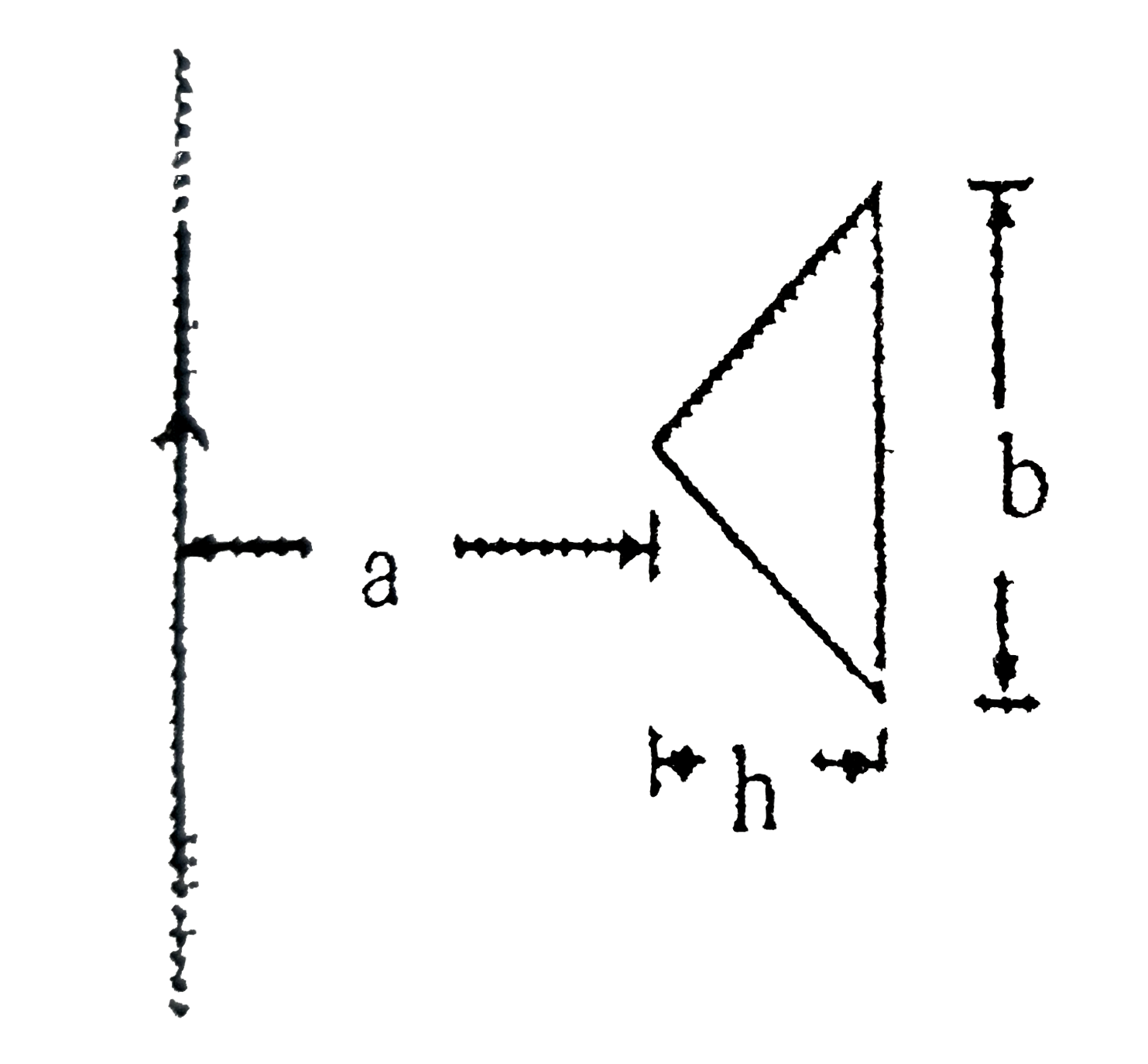
View SolutionA very long staright conductor and an isoceles triangular conductor lie in a plane and separated from each other as shown in the figure.
Given a=10cm, b=20cm and h=10cm
(a) Find their coefficeint of mutual induction.
(b) If current in the staright wire is increasing at a rate of 2A/s , find the direction and magnitude of current in the triangular wire. [Diameter of the wire crosss-section d=1mm, resistivity of the wire, ρ=1.8×10−8Ω−m]
 View Solution
View SolutionTwo long parallel wires are separated by a distance of 2.50cm. The force per unit length that each wire exerts on the other is 4.00×10−5Nm, and the wires repel each other. The current in one wire is 0.600A.
a. What is the current in the second wire ?
b. Are the two currents in the same direction or in opposite direction?View SolutionA body of mass 50 kg, suspended by two strings of lengths 30 cm and 40 cm fastend to two points in the same horizontal line 50 cm apart, is in equilibrium. Find the tension (in Newtons) in each string.
View SolutionTwo long parallel conductors are placed at right angles to a metre scale at the 2cm and 6cm marks, They carry currents of 1A and 3A respectively. They will produce zero magnetic field at the ( ignore the earth's magnetic field )
View SolutionThe two Pt electrodes fitted in a conductance cell are 1.5cm apart while the cross− sectional area of each electrode is 0.75cm. What is the cell constant?
View SolutionThe two Pt electrodes fitted in a conductance cell are 1.5cm apart while the cross− sectional area of each electrode is 0.75cm. What is the cell constant?
View Solution

