Figure shows two current carrying wires piercing the plane of an imaginary loop. One of the wires is normal to the plane of the loop while the other is at an angle. Calculate the net current enclosed.

The current enclosed is simply I1+I2. There is no need to
take any component of I2 perpendicular to the plane of the loop.
All that matters is just the magnitude of the net charge per unit
time that crosses the plane of the loop.
Just as in the case of Gauss's law, the selection of the Amperian
loop is critical for easy application o fhte law. The general rules
while selecting the loop are :
⋅ Estimate the direction of the magnetic field around the
current carrying conductor.
⋅ The loop should include the current carrying element whose
magnetic field is to be calculated.
⋅ The magnetic field should be constant over the whole loop
or should be easy to calculate on the different portions of
the loop.
⋅ The dot product ∮→B.→dl should be easy to calculate.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Solved Example20videos
SOURCES OF MAGNETIC FIELD
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Concept Exercise 2.135videos
SOURCES OF MAGNETIC FIELD
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RAY OPTICSEXERCISE - DPP 1.612videos
RAY OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Comprehension Type14videos
WAVE OPTICS
Similar Questions
Figure shows three current carrying conductors and three imaginary loops. Calculate the current enclosed by each of the loops.
 View Solution
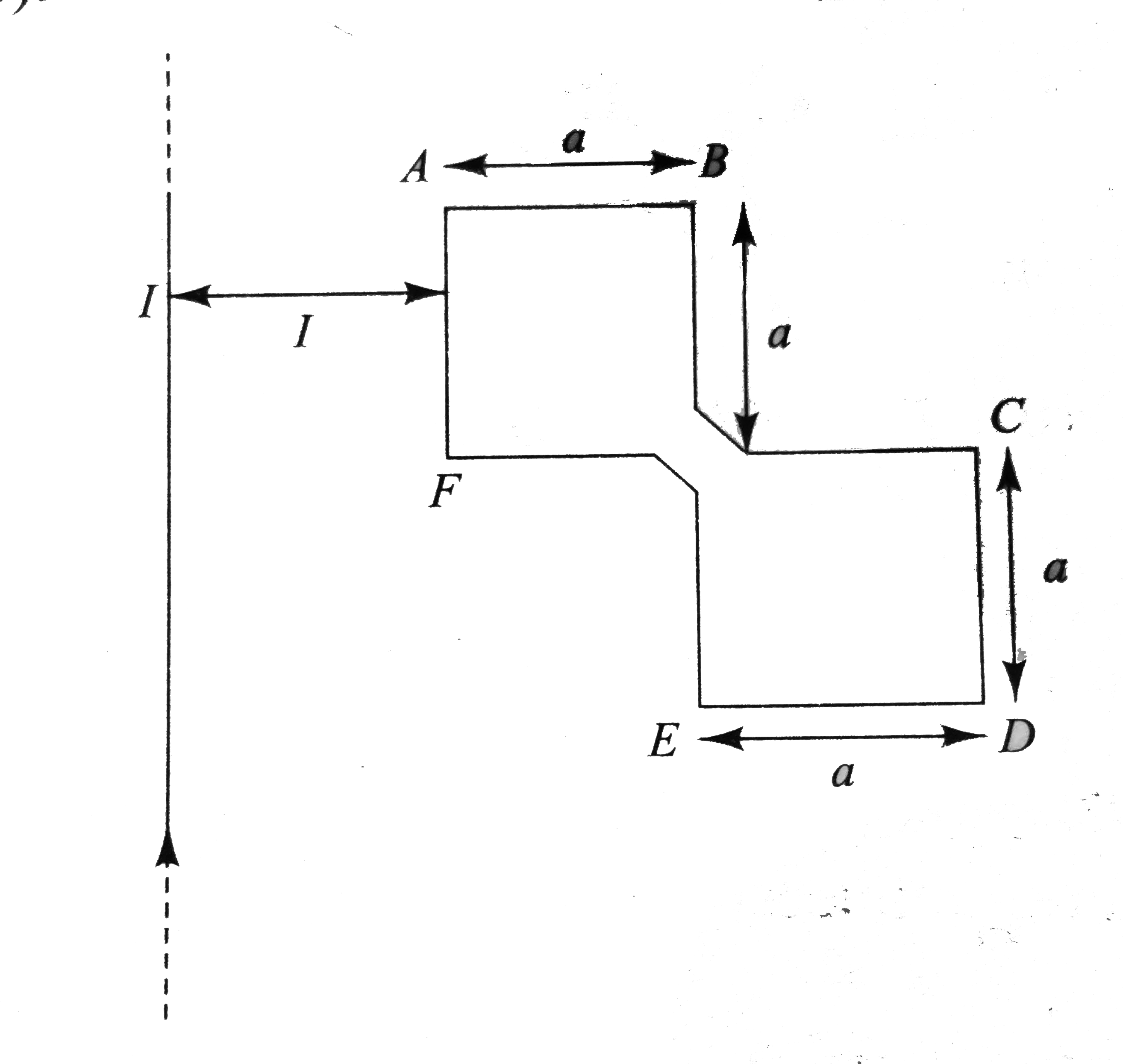
View SolutionIn Fig. there is a conducting loop ABCDEF of resistance λ per unit length placed near a long straight current-carrying wire. The dimension are shows in the figure. The long wire lies in the plane of the loop. The current in the long wire varies as I=I0(t).
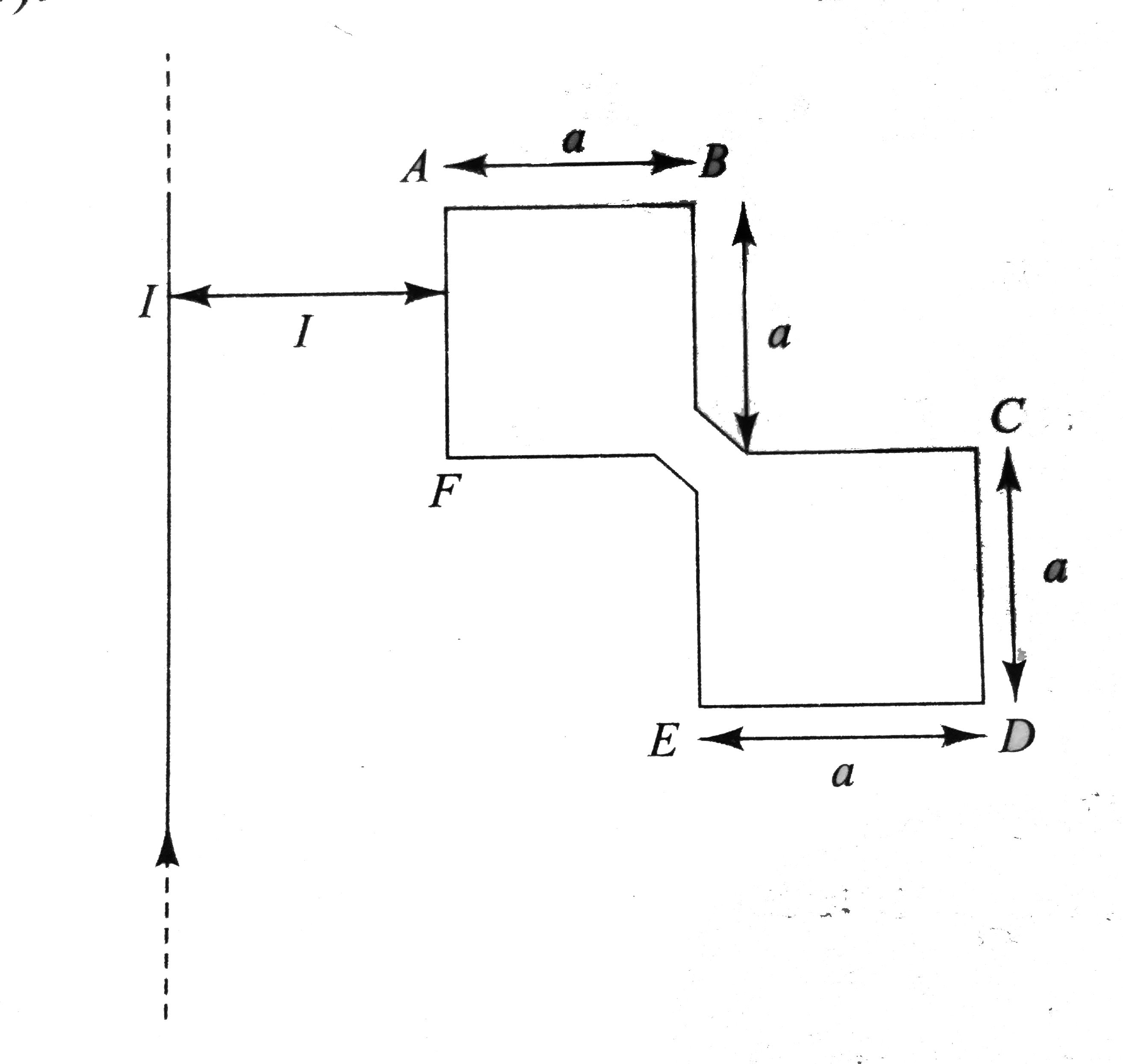
The emf induced in the closed loop isView SolutionIn Fig. there is a conducting loop ABCDEF of resistance λ per unit length placed near a long straight current-carrying wire. The dimension are shows in the figure. The long wire lies in the plane of the loop. The current in the long wire varies as I=I0(t).
The heat produced in the loop in time t isView SolutionIn Fig. there is a conducting loop ABCDEF of resistance λ per unit length placed near a long straight current-carrying wire. The dimension are shows in the figure. The long wire lies in the plane of the loop. The current in the long wire varies as I=I0(t).

The heat produced in the loop in time t isView SolutionShows a long current carrying wire and two rectangular loops moving with of velocity v. Find the direction of current in each loop.
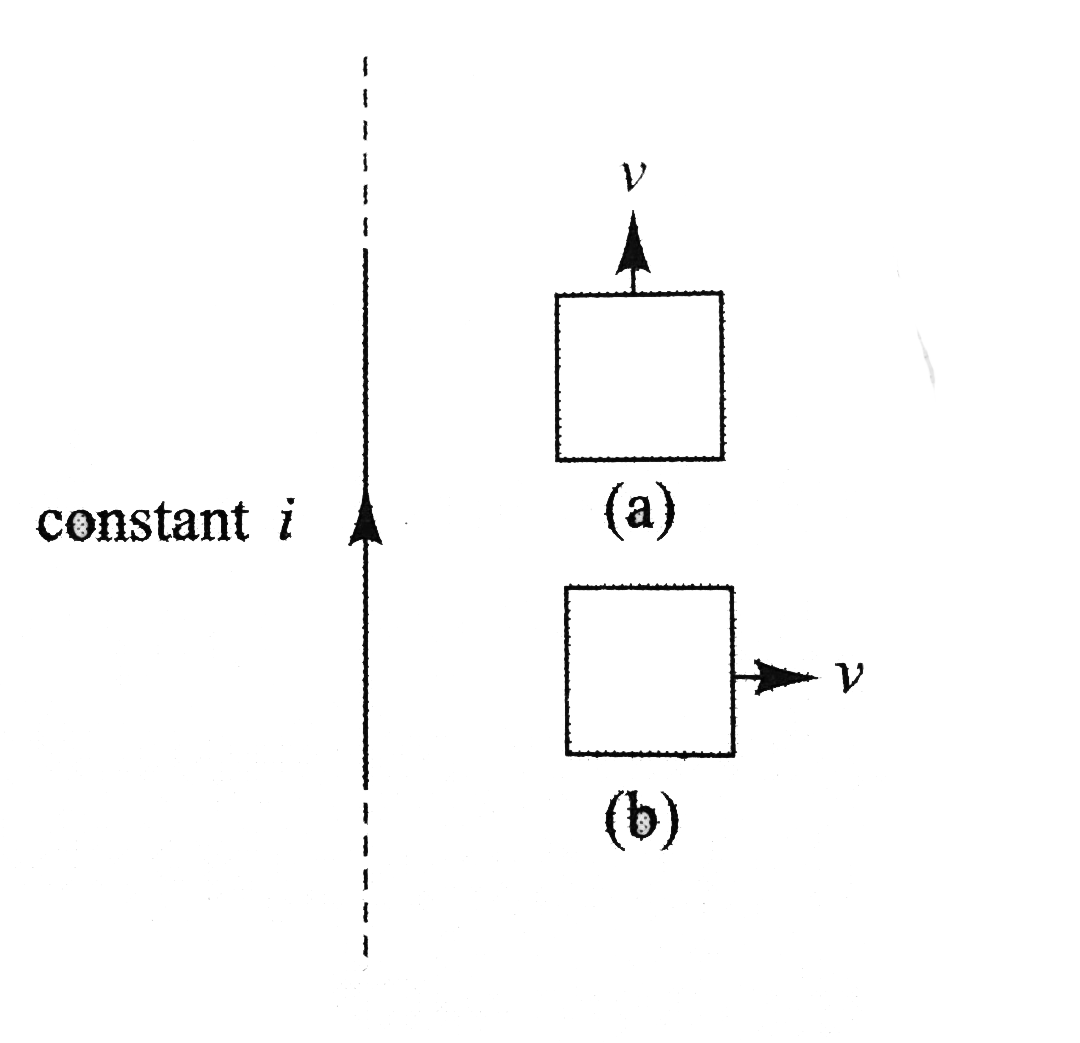 View Solution
View SolutionShows a long current carrying wire and two rectangular loops moving with of velocity v. Find the direction of current in each loop.
 View Solution
View SolutionShows a long current carrying wire and two rectangular loops moving with of velocity v. Find the direction of current in each loop.
 View Solution
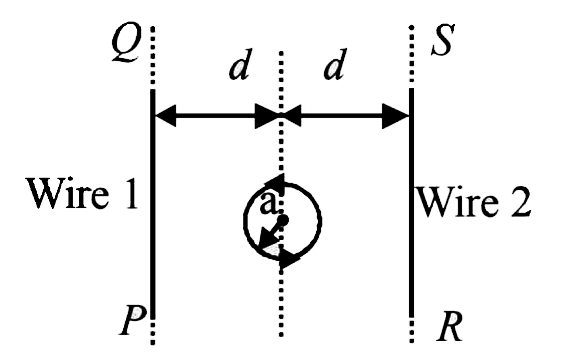
View SolutionThe figure shows a circular loop of radius a with two long parallel wires (νmbered1and2) all in the plane of the paper . The distance of each wire from the centre of the loop is d. The loop and the wire are carrying the same current I. The current in the loop is in the counterclockwise direction if seen from above.
(q) The magnetic fields(B) at P due to the currents in the wires are in opposite directions.
(r) There is no magnetic field at P.
(s) The wires repel each other.
(4) When d≈a but wires are not touching the loop , it is found that the net magnetic field on the axis of the loop at a height h above the loop is zero. In that caseView SolutionThe figure shows a circular loop of radius a with two long parallel wires (νmbered1and2) all in the plane of the paper . The distance of each wire from the centre of the loop is d. The loop and the wire are carrying the same current I. The current in the loop is in the counterclockwise direction if seen from above.
.
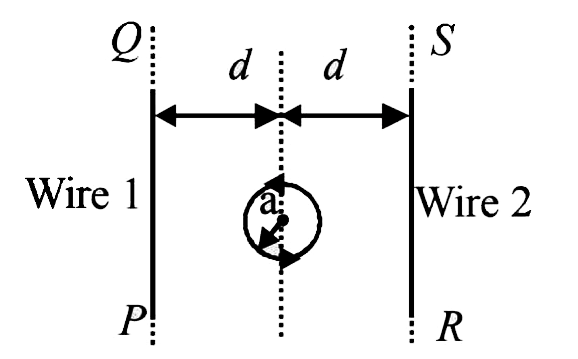
(5) Consider d>>a, and the loop is rotated about its diameter parallel to the wires by 30∘ from the position shown in the figure. If the currents in the wire are in the opposite directions, the torque on the loop at its new position will be ( assume that the net field due to the wires is constant over the loop).View SolutionThe figure shows a circular loop of radius a with two long parallel wires (numbered 1 and 2) all in the plane of the paper . The distance of each wire from the centre of the loop is d. The loop and the wire are carrying the same current I. The current in the loop is in the counterclockwise direction if seen from above.
(q) The magnetic fields(B) at P due to the currents in the wires are in opposite directions.
(r) There is no magnetic field at P.
(s) The wires repel each other.

(4) When d≈a but wires are not touching the loop , it is found that the net magnetic field on the axis of the loop . In that caseView Solution

