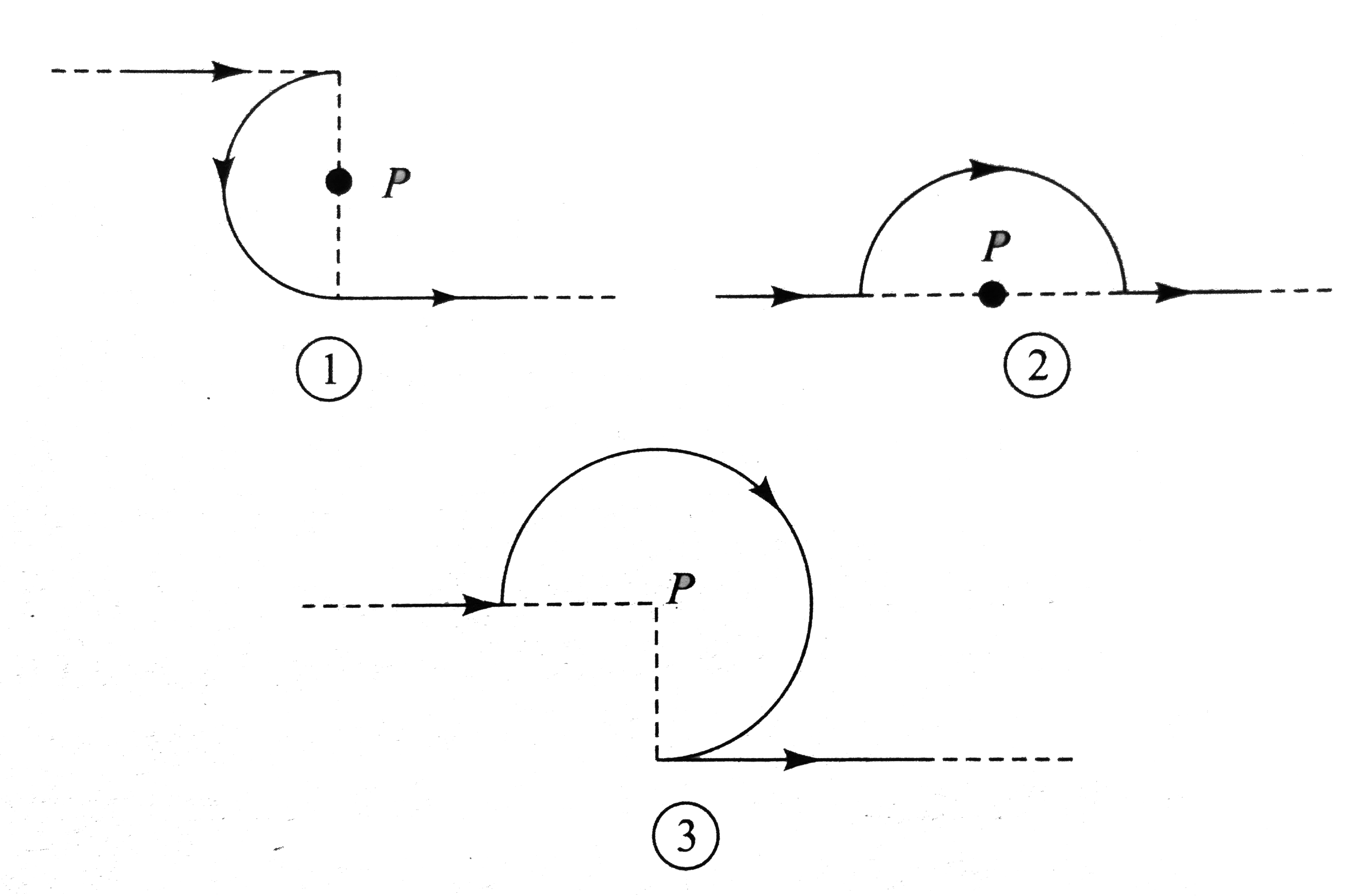
Figure here shows three cases, in all cases the circular path has radius r and straight ones are infinitely long. For same current, the magnetic field at the centre P in cases 1, 2 and 3 have the ratio
(−π2):(π2):(3π4−12)
(−π2+1):(π2+1):(3π4+12)
(−π2):(π2):(3π4)
(−π2−1):(π2−14):(3π4+12)
The correct Answer is:A
(a) →B1=μ0I4r⊙,→B2=μ0I4r⊗
→B3=μ0I2r(34)⊗+μ0I4πr⊙=μ0I4r[32⊗+1π⊙]
=μ0I4r[3π−22π]⊗=μ0I4r(2π)(3π4−12)⊗
B1:B2:B3=−(π2):(π2):(3π4−12)
Topper's Solved these Questions
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Exercise (multiple Currect )
5 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Exercise (assertion-reasioning )
2 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Exercise (subjective )
10 Videos
- RAY OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RAY OPTICSEXERCISE - DPP 1.6
12 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Comprehension Type
14 Videos
Similar Questions
Knowledge Check
A circular coil of radius 10 cm having 100 turns carries a current of 3.2 A. The magnetic field at the center of the coil is
A2.01×10−3TB5.64×10−3TC2.64×10−3TD5.64×10−3T
A circular coil of radius 1⋅5cmcarriesacurrentof1⋅5A. If the coil has 25 turns , find the magnetic field at the centre.
View SolutionA circular coil 'A' has a radius R and the current flowing through it is I.Another circular coil 'B' has a radius 2R and if 2I is the current flowing through it then the magnetic fields at the centre of the circular coil are in the ratio of
View SolutionIn the figure, the current l enters the circular loop of uniform wire of radius r at A and leaves it at B. The magnetic field of the centre of circular loop is

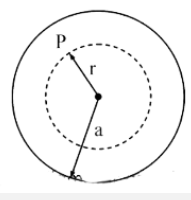
View SolutionThe figure shows the cross-section of a long cylindrical conductor of radius a carrying a uniformly distributed current i. The magnetic field due to current at P is :
View SolutionTwo coils are having magnetic field B and 2B at their centres and current i and 2i then the ratio of their radius is
View SolutionA long wire having a semi-circular loop of radius r carries a current I, as shown in Fig. Find the magnetic field due to entire wire.

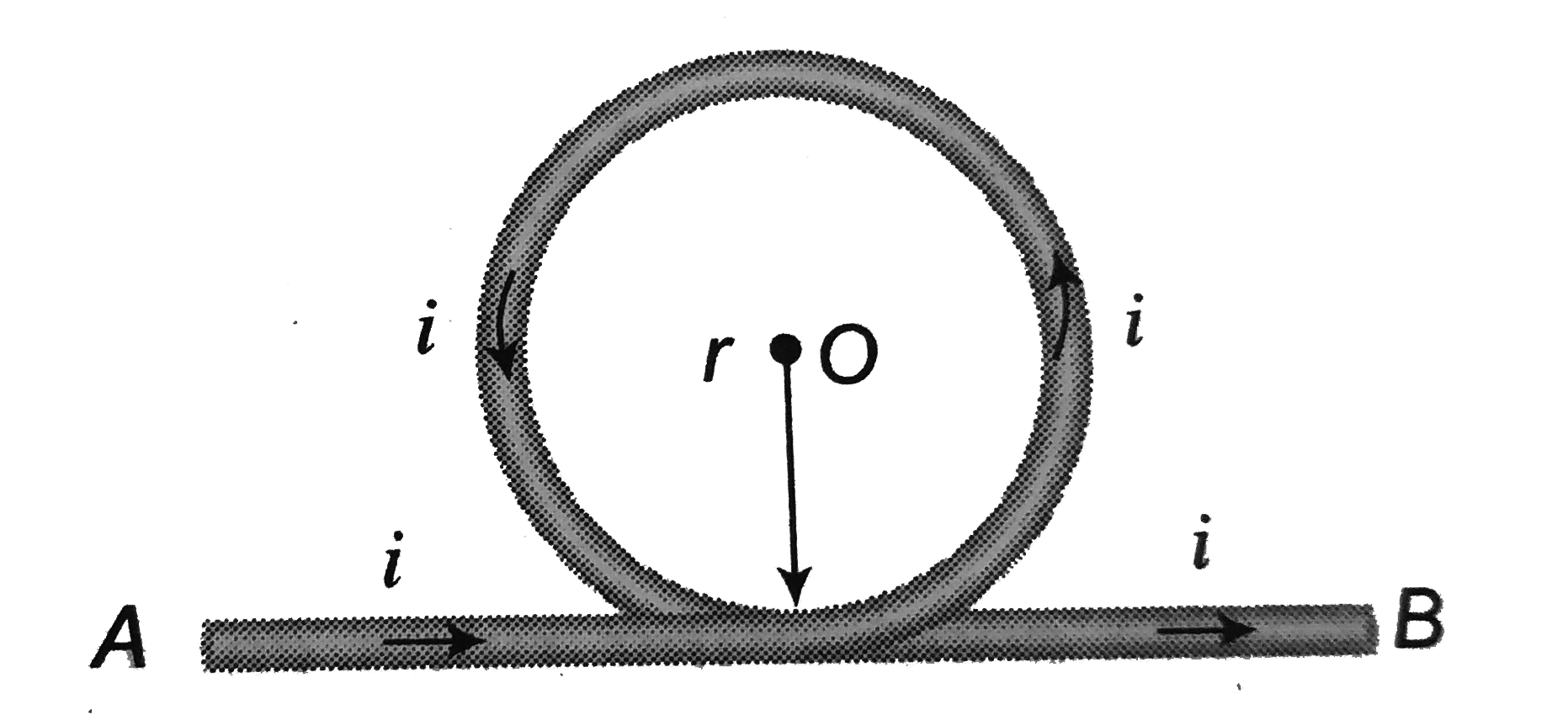
View SolutionA part of a long wire carrying a current i is bent into a circle of radius r as shown in figure. The net magnetic field at the centre O of the circular loop is
View Solution