Repeat the above problem, but with the current in both wires shown in fig. directed into the plane of the figure.
Derive the expression for the magnitude of →B at any point on the x-axis in terms of the x-coordinate of the point. What is the direciton of →B?
√2μ0Iaπ(x2+a2)
3μ0Iaπ(x2+a2)
μ0Ia2π(x2+a2)
μ0Ixπ(x2+a2)
The correct Answer is:D
To solve the problem of finding the magnetic field →B at any point on the x-axis due to two long parallel wires carrying current into the plane of the figure, we will follow these steps:
Step 1: Understand the Configuration
We have two long parallel wires, both carrying current I into the plane of the figure. We need to find the magnetic field at a point P located on the x-axis at a distance x from the midpoint between the two wires.
Step 2: Use the Biot-Savart Law
The magnetic field →B due to a long straight wire at a distance r from the wire carrying current I is given by the formula:
B=μ0I2πr
where μ0 is the permeability of free space.
Step 3: Determine the Distance from Each Wire
Let’s denote the distance from the point P to each wire as r1 and r2. If the wires are separated by a distance 2a, then:
- The distance from the left wire to point P is r1=x+a
- The distance from the right wire to point P is r2=x−a
Step 4: Calculate the Magnetic Field from Each Wire
Using the formula for the magnetic field:
- The magnetic field B1 due to the left wire at point P is:
B1=μ0I2π(x+a)
- The magnetic field B2 due to the right wire at point P is:
B2=μ0I2π(x−a)
Step 5: Determine the Direction of the Magnetic Fields
Using the right-hand rule:
- For the left wire, the magnetic field B1 at point P will be directed out of the plane (positive k-direction).
- For the right wire, the magnetic field B2 at point P will be directed into the plane (negative k-direction).
Step 6: Calculate the Net Magnetic Field
Since B1 is directed out of the plane and B2 is directed into the plane, the net magnetic field Bnet at point P will be:
Bnet=B1−B2
Substituting the values:
Bnet=μ0I2π(x+a)−μ0I2π(x−a)
Step 7: Simplify the Expression
To simplify, we can find a common denominator:
Bnet=μ0I2π((x−a)−(x+a)(x+a)(x−a))
This simplifies to:
Bnet=μ0I2π(−2a(x+a)(x−a))
Thus:
Bnet=−μ0Iaπ(x2−a2)
Step 8: Final Result
The magnitude of the magnetic field →B at any point on the x-axis is:
|→B|=μ0Iaπ(x2−a2)
The direction of →B is in the negative k-direction (into the plane).
We have two long parallel wires, both carrying current I into the plane of the figure. We need to find the magnetic field at a point P located on the x-axis at a distance x from the midpoint between the two wires.
The magnetic field →B due to a long straight wire at a distance r from the wire carrying current I is given by the formula:
B=μ0I2πr
where μ0 is the permeability of free space.
Let’s denote the distance from the point P to each wire as r1 and r2. If the wires are separated by a distance 2a, then:
- The distance from the left wire to point P is r1=x+a
- The distance from the right wire to point P is r2=x−a
Using the formula for the magnetic field:
- The magnetic field B1 due to the left wire at point P is:
B1=μ0I2π(x+a)
- The magnetic field B2 due to the right wire at point P is:
B2=μ0I2π(x−a)
Using the right-hand rule:
- For the left wire, the magnetic field B1 at point P will be directed out of the plane (positive k-direction).
- For the right wire, the magnetic field B2 at point P will be directed into the plane (negative k-direction).
Since B1 is directed out of the plane and B2 is directed into the plane, the net magnetic field Bnet at point P will be:
Bnet=B1−B2
Substituting the values:
Bnet=μ0I2π(x+a)−μ0I2π(x−a)
To simplify, we can find a common denominator:
Bnet=μ0I2π((x−a)−(x+a)(x+a)(x−a))
This simplifies to:
Bnet=μ0I2π(−2a(x+a)(x−a))
Thus:
Bnet=−μ0Iaπ(x2−a2)
The magnitude of the magnetic field →B at any point on the x-axis is:
|→B|=μ0Iaπ(x2−a2)
The direction of →B is in the negative k-direction (into the plane).
Topper's Solved these Questions
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Exercise (integer)
7 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Archives (fill In The Blanks)
1 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Exercise (assertion-reasioning )
2 Videos
- RAY OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RAY OPTICSEXERCISE - DPP 1.6
12 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Comprehension Type
14 Videos
Similar Questions
Repeat the above problem, but with the current in both wires shown in fig. directed into the plane of the figure.
At what value of x is the magnitude of →B is maximum?
View SolutionRepeat the above problem, but with the current in both wires shown in fig. directed into the plane of the figure.
Graph the magnitude of →B at points on the x-axis.
View Solution
Knowledge Check
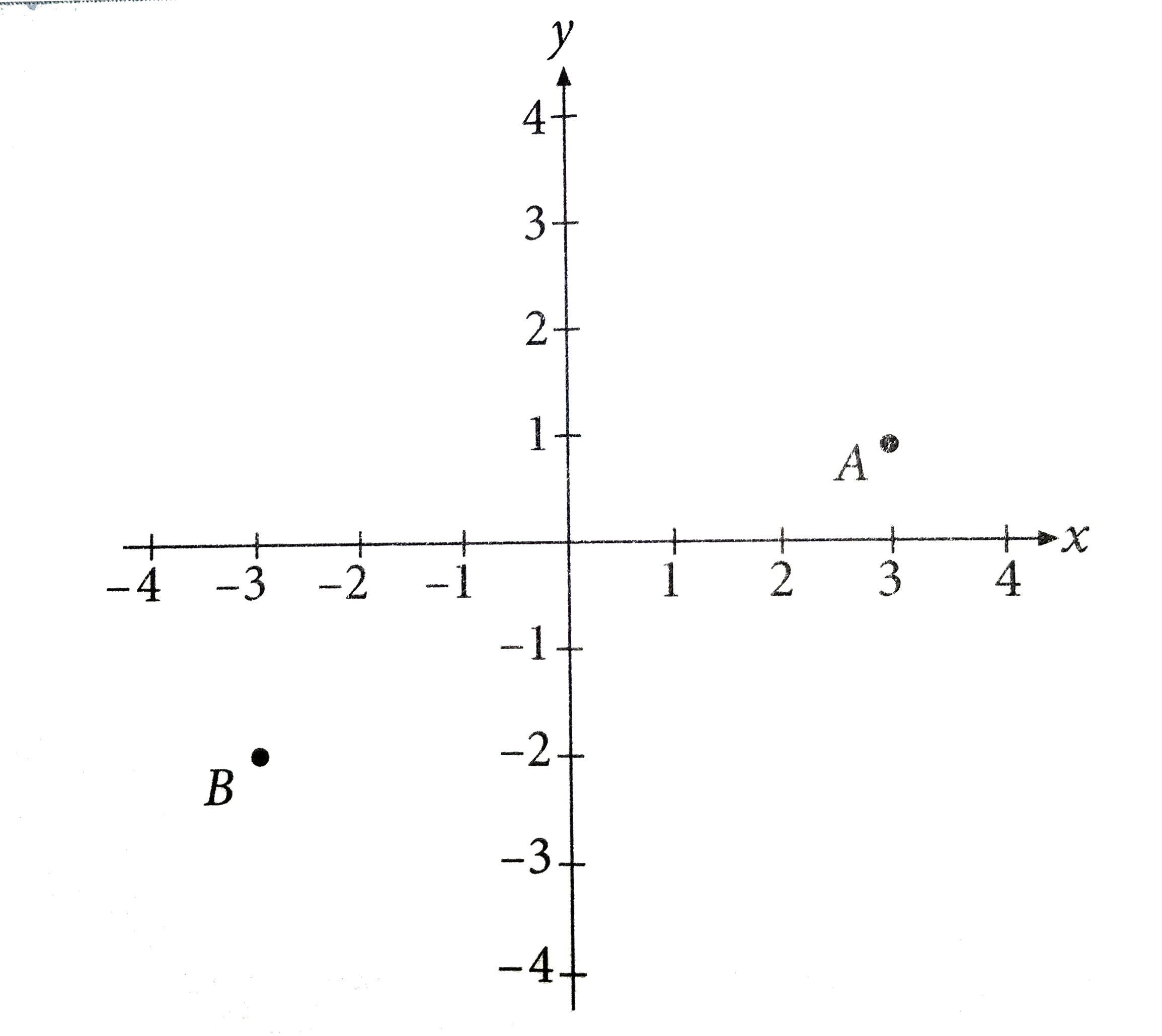
In the xy-plane above, what is the value of the x-coordinates of Point A minus the y-coordinates of Point B?A−2B−1C3D5
Figure shows an end view of two long, parallel wires perpendicular to the xy plane, each carrying a current I, but in opposite directions.

Derive an expression for the magnitude of →B at any point on the x-axis in terms of the x-coordinate of the point. What is the direction of →B?
View SolutionIf a point lies on X-axis, then what are its y and z co-ordinates ?
View Solution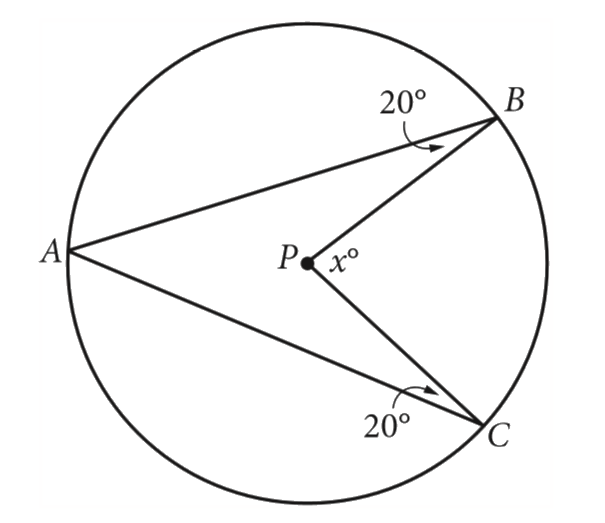
Point P is the centre of the circle in the figure above. What is the value of x?
View SolutionFigure shows an end view of two long, parallel wires perpendicular to the xy plane, each carrying a current I, but in opposite directions.

Graph the magnitude of →B at point on the x-axis.
View SolutionA long straight wire carries a current of 35A. What is the magnitude of the field →B at a point 20cm from the wire?
View SolutionTwo long, straight wires, one above the other, are separated by a distance 2a and are parallel to the x-axis. Let the y-axis be in the plane of the wires in the direction form the lower wire to the upper wire. Each wire carries current I in the +x-direction. What are the magnitude and direction of the net magnetic field of the two wires at a point in the plane of wires:
(a) midway between them?
(b) at a distance a above the upper wire?
(c) at a distance a below the lower wire?
View SolutionWhat is the minimum height of any point on the curve y=x2−4x+6 above the x-axis?
View Solution
