According to Biot-Savarat's law, magentic field due to a straight current carrying wire at a point at a distance r form it is given by
$B = \frac{μ_{0} I}{4 π r} ({\sin ϕ}_{1} + {\sin ϕ}_{2})$
The direction of magnetic field being perpendicular to the plane containing the wire and the point.

Figure, shows a closed loop AOCBA in which current I is flowing as shown. Given $O A = O B = O C = a$ . Find the magnetic field at point B due to this loop.

A

$- \frac{μ_{0} I}{4 π a} (\hat{i} + \hat{k})$

B

$- \frac{μ_{0} I}{4 π a} (\hat{j} + \hat{k})$

C

$- \frac{- μ_{0} I}{2 π a} (\hat{j} + \hat{k})$

D

$\frac{- μ_{0} I}{2 \sqrt{2} π a} (\hat{j} + \hat{k})$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

(c)
At B, magnetic field will be zero due to CB and AB parts.

${\vec{B}}_{A O} = \frac{μ_{0}}{4 π} \frac{I}{a} [{\sin 0}^{\circ} + {\sin 45}^{\circ}] (- \hat{j}) = \frac{- μ_{0} I}{4 π \sqrt{2} a} \hat{j}$
${\vec{B}}_{O C} = \frac{μ_{0}}{4 π} \frac{I}{a} [{\sin 0}^{\circ} + {\sin 45}^{\circ}] (- \hat{k}) = \frac{- μ_{0} I}{4 π \sqrt{2} a} \hat{k}$
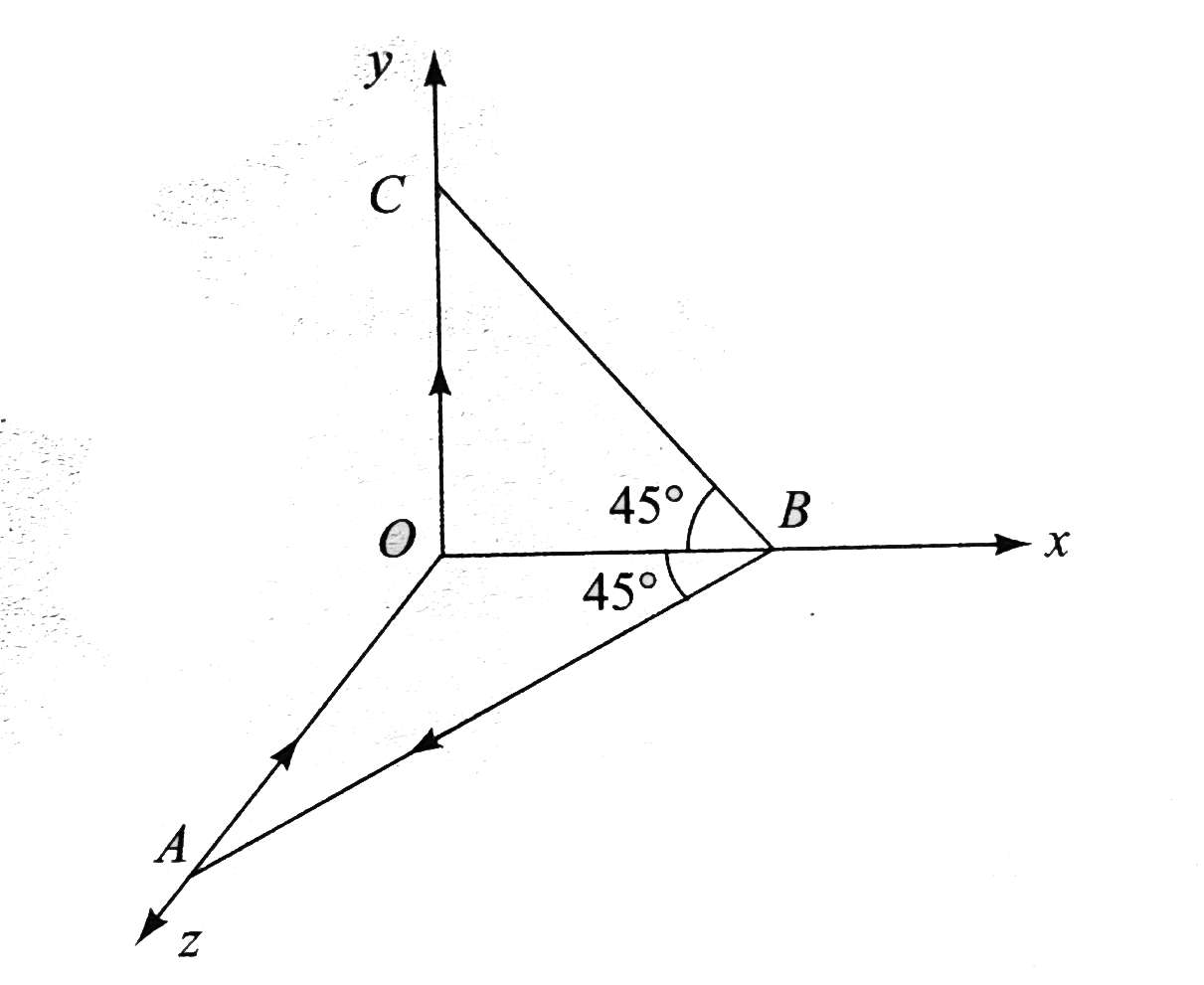
Net magnetic field at B
$= {\vec{B}}_{A O} + {\vec{B}}_{O C} = - \frac{μ_{0} I}{4 π \sqrt{2} a} (\hat{j} + \hat{k})$
At O, magnetic field due to AO and OC will be zero.
Due. to BC: $r = a {\cos 45}^{\circ} = \frac{a}{\sqrt{2}}$
${\vec{B}}_{C B} = \frac{μ_{0}}{4 π} \frac{I}{r} [{\sin 45}^{\circ} + {\sin 45}^{\circ}] (- \hat{k}) = \frac{- μ_{0} I}{2 π a} \hat{k}$
Similarly, due to BA: ${\vec{B}}_{B A} = \frac{- μ_{0} I}{2 π a} \hat{j}$
Net magnetic field $= {\vec{B}}_{C A} + {\vec{B}}_{B A} = \frac{- μ_{0} I}{2 π a} (\hat{j} + \hat{k})$

|

Updated on:21/07/2023

Class 12 PHYSICS MOVING CHARGES AND MAGNETISM

Topper's Solved these Questions

Similar Questions

CENGAGE PHYSICS ENGLISH-SOURCES OF MAGNETIC FIELD-Exercise (linked Comprehension)

Home
Ask Doubt
Profile