Ampere's law provides us an easy way to calculate the magnetic field due to a symmetrical distribution of current. Its mathemfield expression is ∮→B.dl=μ0Iin.
The quantity on the left hand side is known as line as integral of magnetic field over a closed Ampere's loop.
Only the current inside the Amperian loop contributes in
finding magnetic field at any point on the Ampere's loop
line integral of magnetic field
in both of the above
in neither of them
The correct Answer is:B
To solve the question regarding Ampere's Law and the contributions of current to the magnetic field, we will analyze each option provided in the context of the law itself.
1. Understanding Ampere's Law:
Ampere's Law states that the line integral of the magnetic field →B around a closed loop (Ampere's loop) is equal to μ0 times the total current Iin that passes through the surface enclosed by the loop. Mathematically, it is expressed as:
∮→B⋅d→l=μ0Iin
2. Analyzing the Options:
- Option A: "Finding magnetic field at any point on the Ampere loop."
- This option suggests that only the current inside the loop contributes to the magnetic field at any point on the loop. However, while the current inside the loop does contribute to the magnetic field, currents outside the loop can also influence the field at points on the loop, but they do not contribute to the integral. Therefore, this option is incorrect.
- Option B: "Line integral of the magnetic field."
- This option refers to the expression ∮→B⋅d→l, which is indeed the line integral of the magnetic field around the closed loop. This is a correct statement as it directly reflects the mathematical formulation of Ampere's Law. Thus, this option is correct.
- Option C: "Both of the above."
- Since Option A is incorrect, this option cannot be correct either. Therefore, this option is incorrect.
- Option D: "Neither of them."
- Since we have established that Option B is correct, this option is also incorrect.
3. Conclusion:
The correct answer to the question is Option B, which accurately describes the line integral of the magnetic field as per Ampere's Law.
Ampere's Law states that the line integral of the magnetic field →B around a closed loop (Ampere's loop) is equal to μ0 times the total current Iin that passes through the surface enclosed by the loop. Mathematically, it is expressed as:
∮→B⋅d→l=μ0Iin
- Option A: "Finding magnetic field at any point on the Ampere loop."
- This option suggests that only the current inside the loop contributes to the magnetic field at any point on the loop. However, while the current inside the loop does contribute to the magnetic field, currents outside the loop can also influence the field at points on the loop, but they do not contribute to the integral. Therefore, this option is incorrect.
- This option refers to the expression ∮→B⋅d→l, which is indeed the line integral of the magnetic field around the closed loop. This is a correct statement as it directly reflects the mathematical formulation of Ampere's Law. Thus, this option is correct.
- Since Option A is incorrect, this option cannot be correct either. Therefore, this option is incorrect.
- Since we have established that Option B is correct, this option is also incorrect.
The correct answer to the question is Option B, which accurately describes the line integral of the magnetic field as per Ampere's Law.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Exercise (integer)7videos
SOURCES OF MAGNETIC FIELD
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Archives (fill In The Blanks)1videos
SOURCES OF MAGNETIC FIELD
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Exercise (assertion-reasioning )2videos
SOURCES OF MAGNETIC FIELD
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RAY OPTICSEXERCISE - DPP 1.612videos
RAY OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Comprehension Type14videos
WAVE OPTICS
Similar Questions
Ampere's law provides us an easy way to calculate the magnetic field due to a symmetrical distribution of current. Its mathemfield expression is ∮→B.dl=μ0Iin.
The quantity on the left hand side is known as line as integral of magnetic field over a closed Ampere's loop.
If the current density in a linear conductor of radius a varies with r according to relation J=kr2, where k is a constant and r is the distance of a point from the axis of conductor, find the magnetic field induction at a point distance r from the axis when rlta. Assume relative permeability of the conductor to be unity.View SolutionAmpere's law provides us an easy way to calculate the magnetic field due to a symmetrical distribution of current. Its mathemfield expression is ∮→B.dl=μ0Iin.
The quantity on the left hand side is known as line as integral of magnetic field over a closed Ampere's loop.
In the above question, find the magnetic field induction at a point distance r from the axis when rgta. Assume relative permeability of the medium surrounding the conductor to be unity.View SolutionA: In any magnetic field region the line integral ∮→B.→dl along a closed loop is always zero.
R: The magnetic field →B in the expressioin ∮→B.→dl is due to the currents enclosed only by the loop.View SolutionIn Ampere's law (∮(→B).(→dl))=(μ0)I, the current outside the curve is not included on the right hand side. Does it mean that the magnetic field B calculated by using Ampere's law , gives the contribution of only the currents crossing the area bounded by the curve?
View SolutionA: When currents vary with time, Newton's third law is valid only if momentum carried by the electromagnetic field is taken into account.
R: Magnetic field lines always form closed loops.View SolutionThree distinct current carrying wires intersect a finite rectangular plane ABCD. The current in left wire and the loop is I1. The direction of current in left most wire and right most loop is downwards as shown in figure. The current I2 through middle wire is adjusted so that the path integral of the total magnetic field along the perimeter of the rectangle is zero, that is, ∮ABCDA→B.→dl=0. Then the current I2 is-
A. 2I1 and upwards
B. 2I1 and downwards
C. 4I1 and upwards
D. 3I1 and downwardsView SolutionIf →B1,→B2 and →B3 are the magnetic field due to l1,l2 and l3, then in Ampere's circuital law ∮→B.→dl=μ0l,→B is
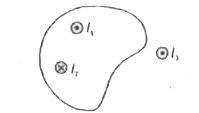View Solution(a)Using Ampere's circuital law, obtain the expression for the magnetic field due to a long solenoid at a point inside the solenoid on its axis.
(b )How is the magnetic field inside a given solenoid made strong?View SolutionIf →B1,→B2,→B3and→B4 are the magnetic field due to current I1,I2,I3andI4respectively then in ampere circuital law ∮→B.d→l=μ0I, →B is
_PHY_E06_049_Q01.png)
View Solution(a) A closed loop is held stationary in the magnetic field between the north and south poles of two permanent magnets held fixed. Can we hope to generate current in the loop by using very strong magnets?
(b) A closed loop moves normal to the constant electric field between the plates of a large capacitor. Is a current induced in the loop (i) when it is wholly inside the region between the capacitor plates (ii) when it is partially outside the plates of the capacitor? The electric field is normal to the plane of the loop.
(c) A rectangular loop and a circular loop are moving out of a uniform magnetic field region (Fig. 6.8) to a field-free region with a constant velocity v. In which loop do you expect the induced emf to be constant during the passage out of the field region? The field is normal to the loops.
(d) Predict the polarity of the capacitor in the situation described by Fig. 6.9.
View Solution