If →B1,→B2 and →B3 are the magnetic field due to l1,l2 and l3, then in Ampere's circuital law ∮→B.→dl=μ0l,→B is

→B=→B1−→B2
→B=→B1+→B2+→B3
→B=→B1−→B2+→B3
→B=→B3
The correct Answer is:B
Step by step video & image solution for If vecB_(1),vecB_(2) and vecB_(3) are the magnetic field due to l_(1),l_(2) and l_(3), then in Ampere's circuital law ointvecB.vec(dl)=mu_(0)l, vecB is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MOVING CHARGE AND MAGNESIUMBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOVING CHARGE AND MAGNESIUMEXERCISE - SECTION C
47 Videos
- MOVING CHARGE AND MAGNESIUMBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOVING CHARGE AND MAGNESIUMEXERCISE - SECTION D
16 Videos
- MOVING CHARGE AND MAGNESIUMBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOVING CHARGE AND MAGNESIUMEXERCISE - ASSIGNMENT (SECTION A)
34 Videos
- MOTION IN STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN STRAIGHT LINEEXERCISE - Assignment (SECTION - J)
2 Videos
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Assignment Section J (Aakash Challengers Questions)
5 Videos
Similar Questions
If →B1,→B2,→B3and→B4 are the magnetic field due to current I1,I2,I3andI4respectively then in ampere circuital law ∮→B.d→l=μ0I, →B is
_PHY_E06_049_Q01.png)
View SolutionThe base vectors →a1,→a2 and →a3 are given in terms of base vectors →b1,→b2 and →b3 as →a1=2→b1+3→b2−→b3, →a2=→b1−2→b2+2→b3 and →a3=2→b1+→b2−2→b3, if →F=3→b1−→b2+2→b3, then vector →F in terms of →a1,→a2 and →a3 is
View SolutionA: In any magnetic field region the line integral ∮→B.→dl along a closed loop is always zero.
R: The magnetic field →B in the expressioin ∮→B.→dl is due to the currents enclosed only by the loop.
View SolutionLet BP and BQ be the magnetic field produced by the wire P and Q which are placed symmetrically in a rectangular loop ABCD as shown in figure.Current in wire P is I directed inward and in Q is 2I directed outwards.if ∫BA→BQ.→dl=2μ0 tesla meter,∫AD→BP.→dl=−2μ0 tesla meter,&∫BA→BP.→dl=−μ0 tesla meter tesla meter the value of I will be:
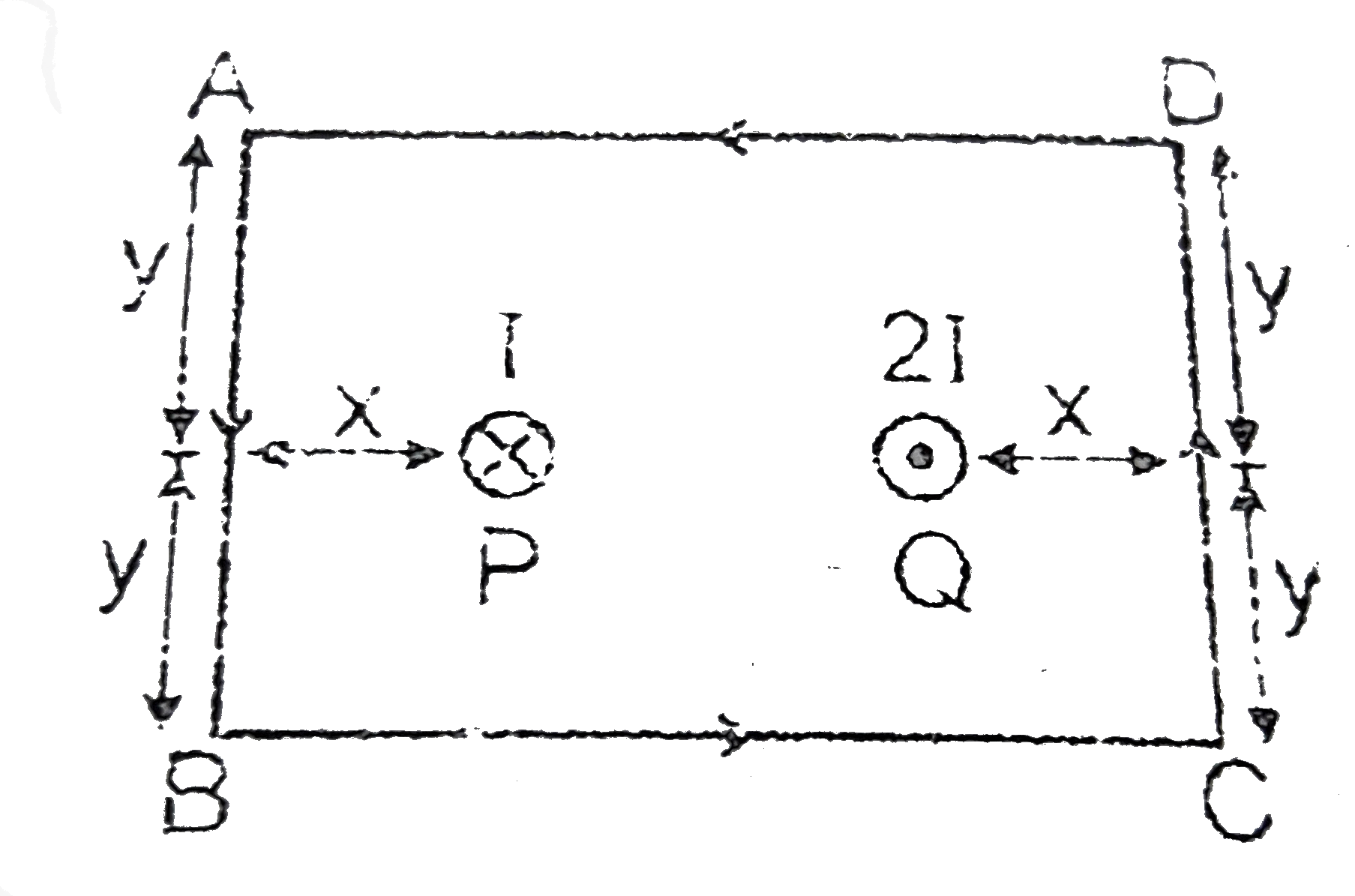
View SolutionIf −→|a|=3,∣∣→b∣∣=4,and∣∣→a+→b∣∣=5,then∣∣→a−→b∣∣ is equal to (A) 6 (B) 5 (C) 4 (D) 3
View SolutionIf →r=x1(→a×→b)+x2(→b×→a)+x3(→c×→d)and4[→a→b→c]=1 then x1+x2+x3 is equal to
View SolutionIf →a,→b and →c are three vectors such that →a+→b=→c and further a2+b2=c2, find the angle between them →a and →b ?
View Solution(→A+2→B).(2→A−3→B):-
View SolutionIf →aand→b are non zero, non collinear vectors and →a1=λ→a+3→b,→b1=2→a+λ→b,→c1=→a+→b. Find the sum of all possible real values of λ so that points A1,B1,C1 whose position vectors are →a1,→b1,→c1 respectively are collinear is equal to.
View SolutionIf →a,→band→c are any three non-coplanar vectors, then prove that points l1→a+m1→b+n1→c,l2→a+m2→b+n2→c,l3→a+m3→b+n3→c,l4→a+m4→b+n4→c are coplanar if ∣∣ ∣ ∣ ∣∣l1l2l3l4m1m2m3m4n1n2n3n41111∣∣ ∣ ∣ ∣∣=0
View Solution
