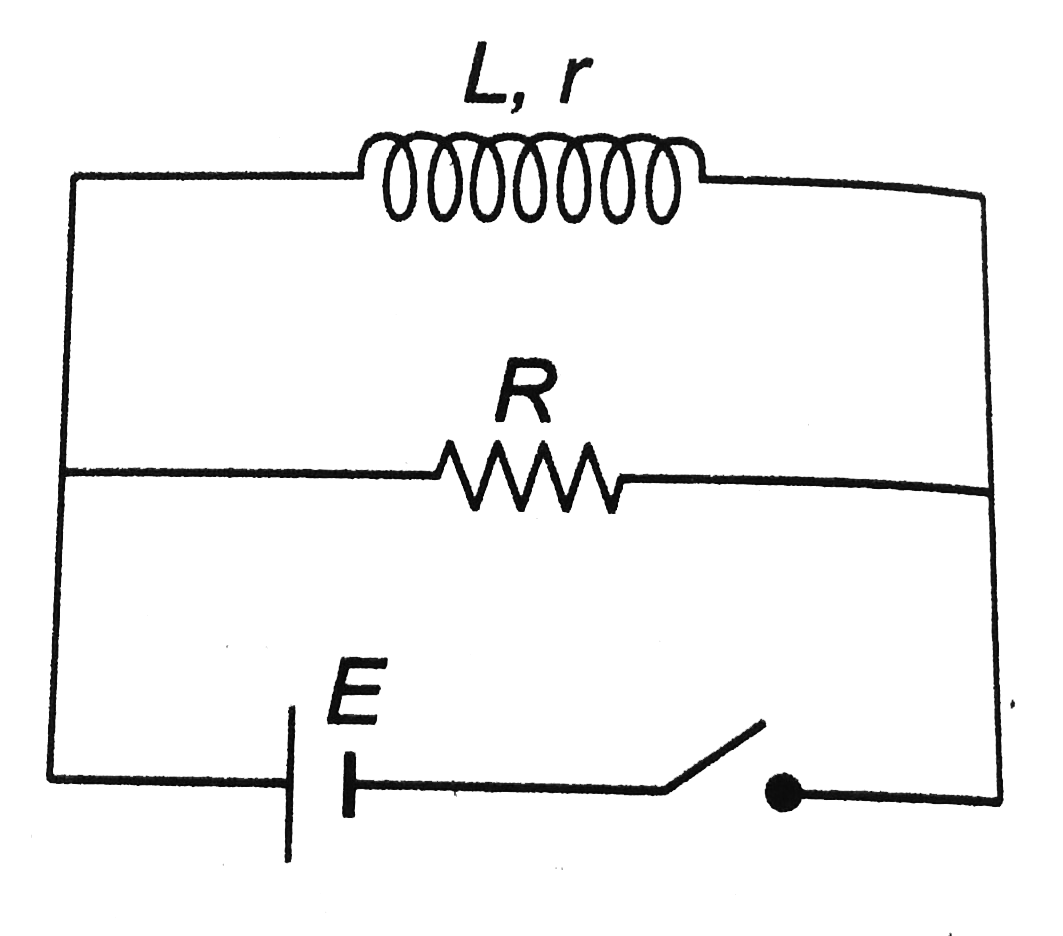
A solenoid of inductance with resistance is connected in parallel to a resistance . A battery of emf and of negligible internal resistance is connected across the parallel combination as shown in the figure. At time , switch is opened, calculate
(a) current through the solenoid after the switch is opened.
(b) amount of heat generated in the solenoid.
Current in the inductor just after removing the battery is
Total enery dissipated in the solenoid and the reistor long time after removing the battery is
The amount of heat generated in the solenoid due to removing the battery is
The amount of heat generated in the solenoid due to removing the battery is
The correct Answer is:C
Applying in outer loop, we get
Initial energy in solenoid This
energy will be dissipared in the from of heat in and after opening of the switch. Since the same current flows through these resistances, therefore heat generated in each resistor is directly proprtional to its resistance.
Heat generated in solenoid
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Exercises (multiple Correct )7videos
INDUCTANCE
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Exercises (assertion-reasoning)2videos
INDUCTANCE
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Exercises (subjective)7videos
INDUCTANCE
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit27videos
HEATING EFFECT OF CURRENT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Multiple Correct Answer type2videos
MAGNETIC FIELD AND MAGNETIC FORCES
Similar Questions
A 5 V battery of negligible internal resistance is connected across a 200 V battery and a resistance of 39Ω as shown in the figure. Find the value of the current.
 View Solution
View Solution
Two batteries of E1 internal resistance r1 & emf E2 internal resistance r2 are connected in parallel and makes a battery system. An external resistance R is connected across this system as shown in the figure.View SolutionA 10 V battery of negilgible internal resistance is connected across a 200V battery and a resistance of 38Ω as shown in figure.
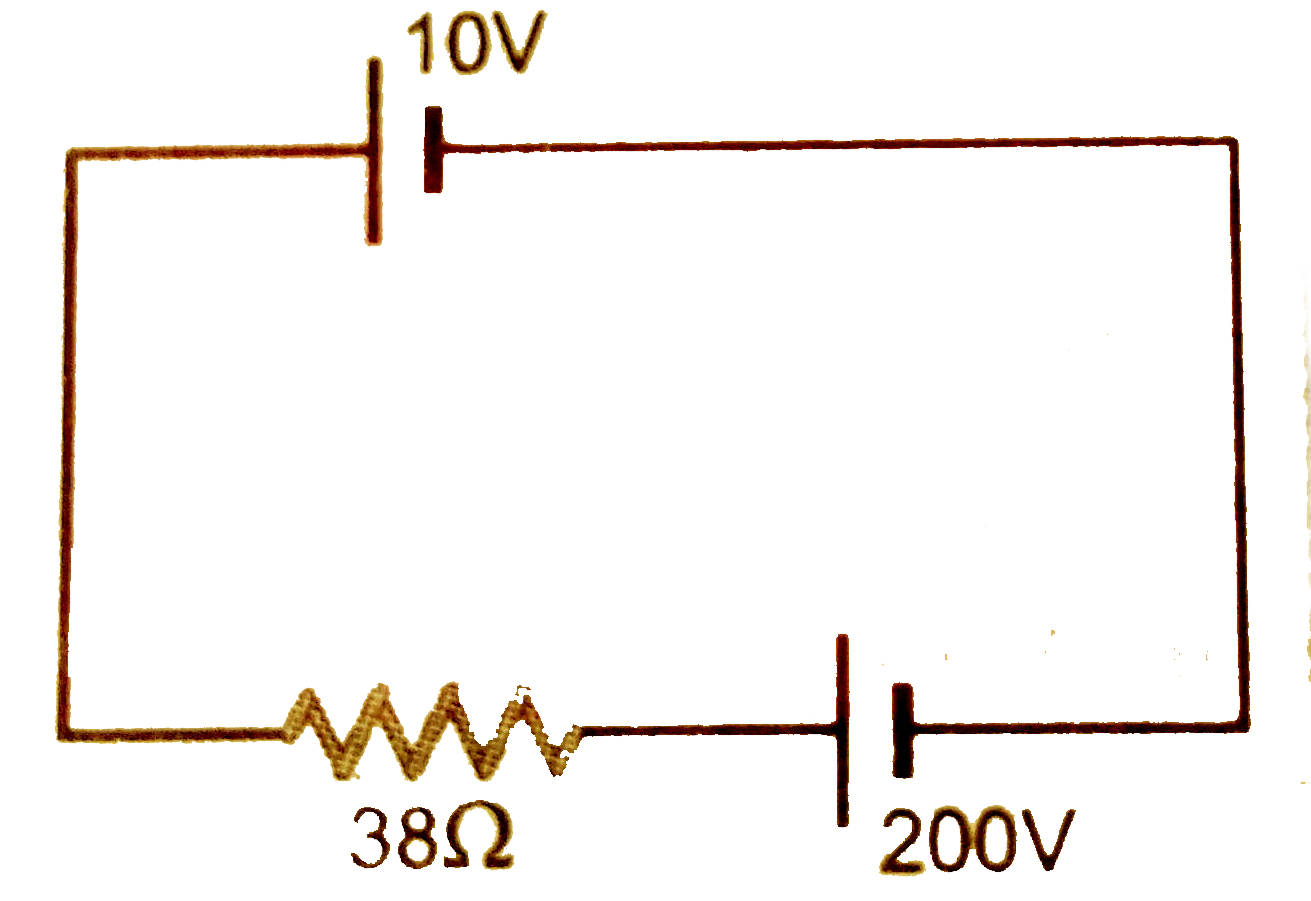 . Find the value of current in the circuit.View Solution
. Find the value of current in the circuit.View SolutionA resistor R is conneted to a parallel combination of two identical batteries each with emf E and an internal resistance r. The potential drop across the resistance R is.
View SolutionA series combination of L and R is connected to a battery of emf E having negligible internal resistance. The final value of current depends upon
View SolutionA battery of emf 2V and internal resistance 0.5(Ω)is connected across a resistance 1.5(Ω). Find the current flow through battery ?
View SolutionA solenoid of resistance R and inductance L has a piece of soft iron inside it. A battery of emf E and of negligible internal resistance is connected across the solenoid as shown in Fig. At any instant, the piece of soft iron is pulled out suddenly so that inductance of the solenoid decrease to ηL(η<1) with battery remaining connected.
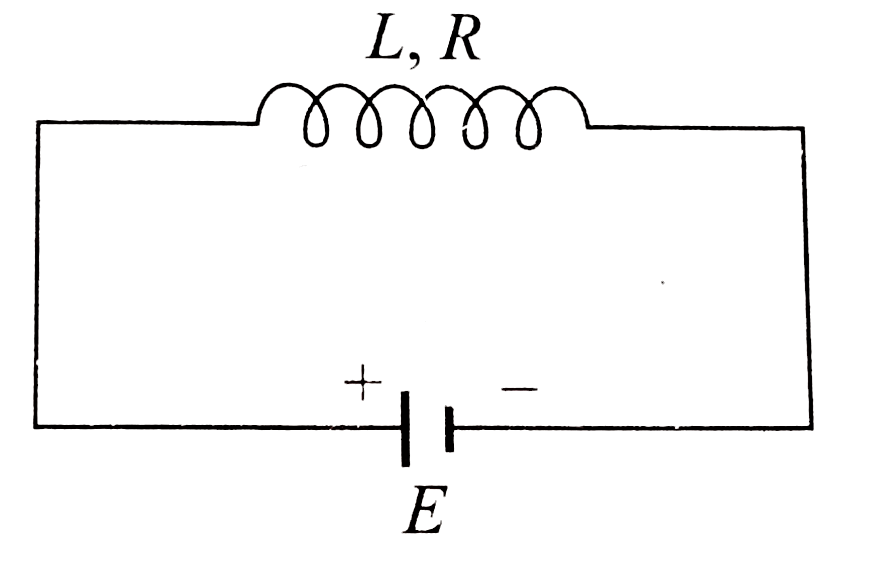
Assume t = 0 is the instant when iron piece has been pulled out, the current as a function of time after this isView SolutionA solenoid of resistance R and inductance L has a piece of soft iron inside it. A battery of emf E and of negligible internal resistance is connected across the solenoid as shown in Fig. At any instant, the piece of soft iron is pulled out suddenly so that inductance of the solenoid decrease to ηL(η<1) with battery remaining connected.
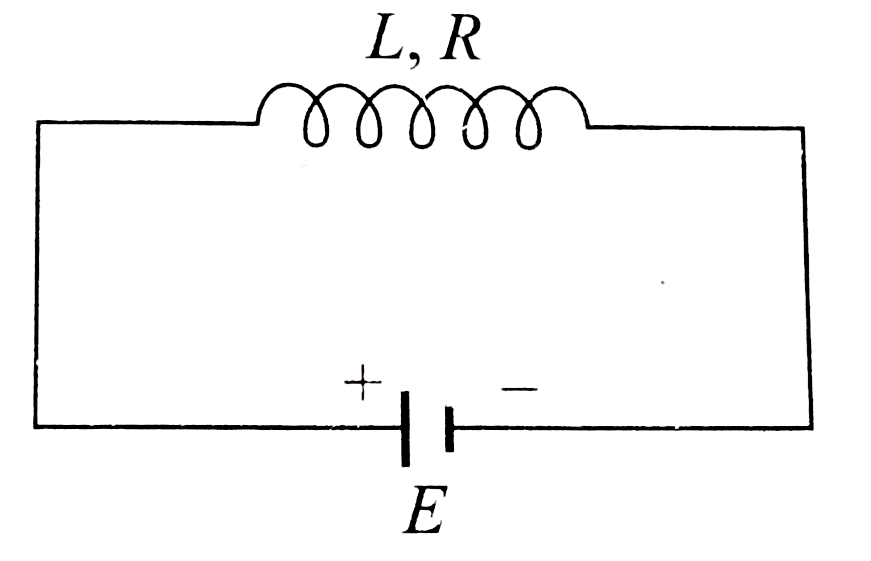
Power supplied by the battery as a function of timeView SolutionA solenoid of resistance R and inductance L has a piece of soft iron inside it. A battery of emf E and of negligible internal resistance is connected across the solenoid as shown in Fig. At any instant, the piece of soft iron is pulled out suddenly so that inductance of the solenoid decrease to ηL(η<1) with battery remaining connected.
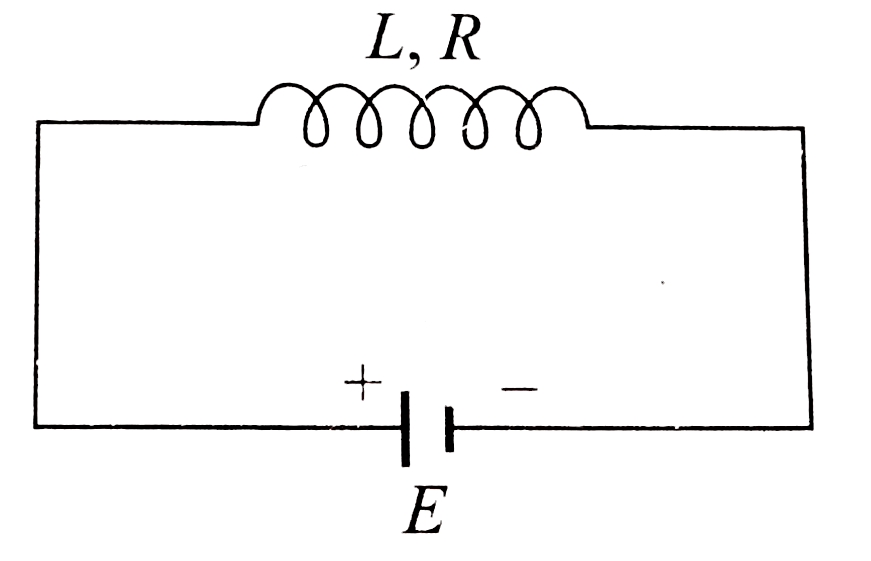
The work done to pull out the soft iron piece isView SolutionA 10 V cell of neglible internal resitsance is connected in parallel across a battery of emf 200 V and internal resistance 38Ω as shown in the figure. Find the value of current in the circuit.
 View Solution
View Solution

