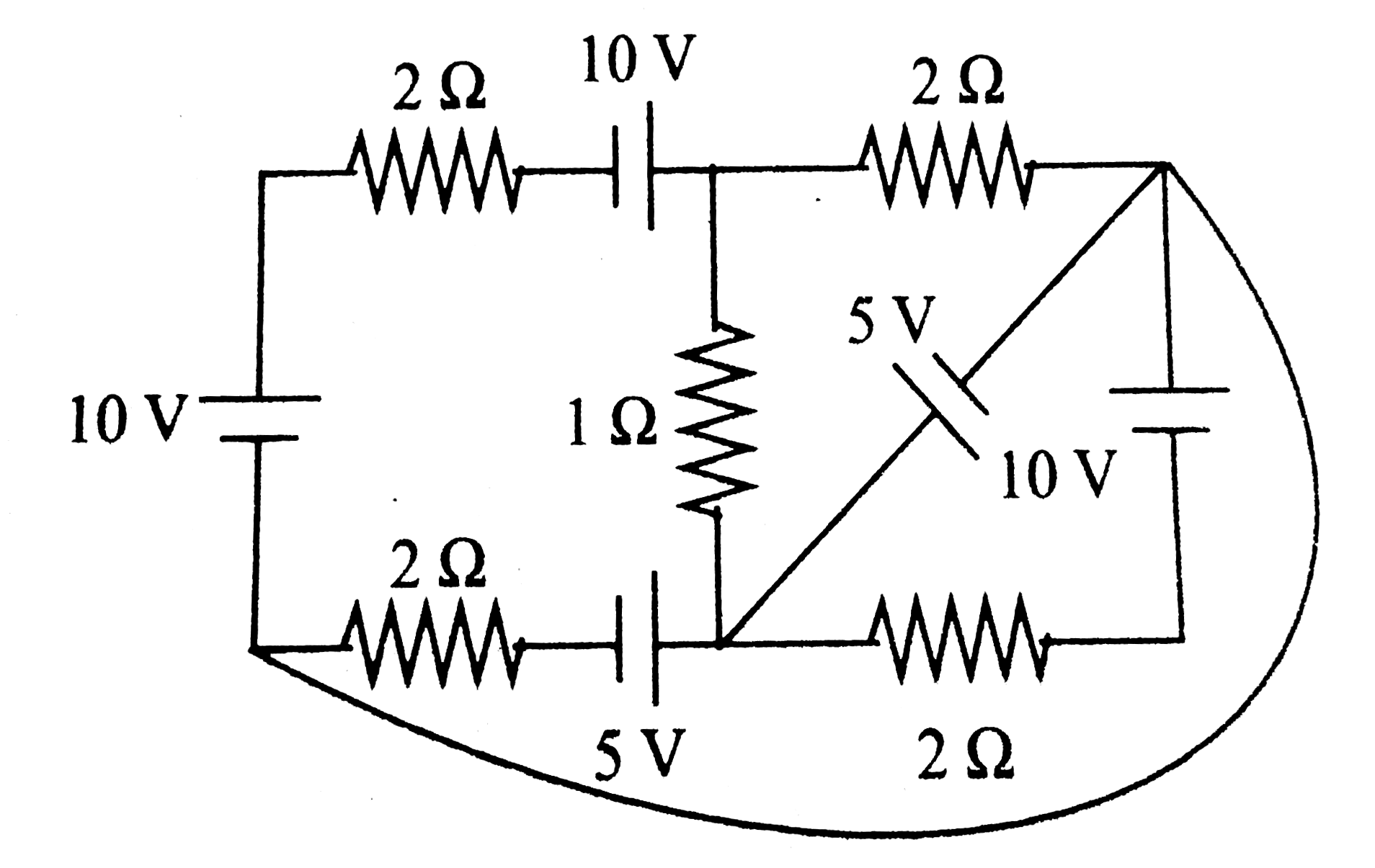
Suppose the 19Ω resistor of the previous problem is disconnected. Find the current through P2Q2 in the two situations (a) and (b) of that problem.
zero
3 mA
1 mA
None of these
The correct Answer is:A
To solve the problem, we need to analyze the circuit after disconnecting the 19 ohm resistor and find the current through points P2 and Q2 in both situations (a) and (b) as described in the previous problem.
1. Understanding the Circuit Configuration:
- We have a circuit with resistors and points P1, P2, Q1, and Q2.
- The 19 ohm resistor is disconnected, which may affect the current flow in the circuit.
2. Analyzing Situation (a):
- In situation (a), it is mentioned that the circuit is incomplete. This implies that there is no closed loop for current to flow.
- Since the circuit is open, the current through P2Q2 will be 0 A.
3. Analyzing Situation (b):
- In situation (b), the circuit is complete, and we can calculate the current through P2Q2.
- We assume that there are two 2 ohm resistors in parallel connected to a voltage source (let's say V).
- The equivalent resistance (R_eq) of two 2 ohm resistors in parallel is given by:
Req=112+12=1 ohm
4. Calculating the Current:
- If the voltage across the circuit is V (let's assume V = 1V for calculation), the current (I) through the equivalent resistance can be calculated using Ohm's Law:
I=VReq=1V1 ohm=1 A
- Therefore, the current through P2Q2 in situation (b) is 1 A.
Final Answers:
- For situation (a): Current through P2Q2 = 0 A
- For situation (b): Current through P2Q2 = 1 A
- We have a circuit with resistors and points P1, P2, Q1, and Q2.
- The 19 ohm resistor is disconnected, which may affect the current flow in the circuit.
- In situation (a), it is mentioned that the circuit is incomplete. This implies that there is no closed loop for current to flow.
- Since the circuit is open, the current through P2Q2 will be 0 A.
- In situation (b), the circuit is complete, and we can calculate the current through P2Q2.
- We assume that there are two 2 ohm resistors in parallel connected to a voltage source (let's say V).
- The equivalent resistance (R_eq) of two 2 ohm resistors in parallel is given by:
Req=112+12=1 ohm
- If the voltage across the circuit is V (let's assume V = 1V for calculation), the current (I) through the equivalent resistance can be calculated using Ohm's Law:
I=VReq=1V1 ohm=1 A
- Therefore, the current through P2Q2 in situation (b) is 1 A.
- For situation (a): Current through P2Q2 = 0 A
- For situation (b): Current through P2Q2 = 1 A
Topper's Solved these Questions
- MISCELLANEOUS VOLUME 5BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Integer
12 Videos
- MISCELLANEOUS VOLUME 5BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Multiple Correct
34 Videos
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - True and False
3 Videos
- NUCLEAR PHYSICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NUCLEAR PHYSICSEXERCISE - ddp.5.5
14 Videos
Similar Questions
Find the current through 12Ω resistor in
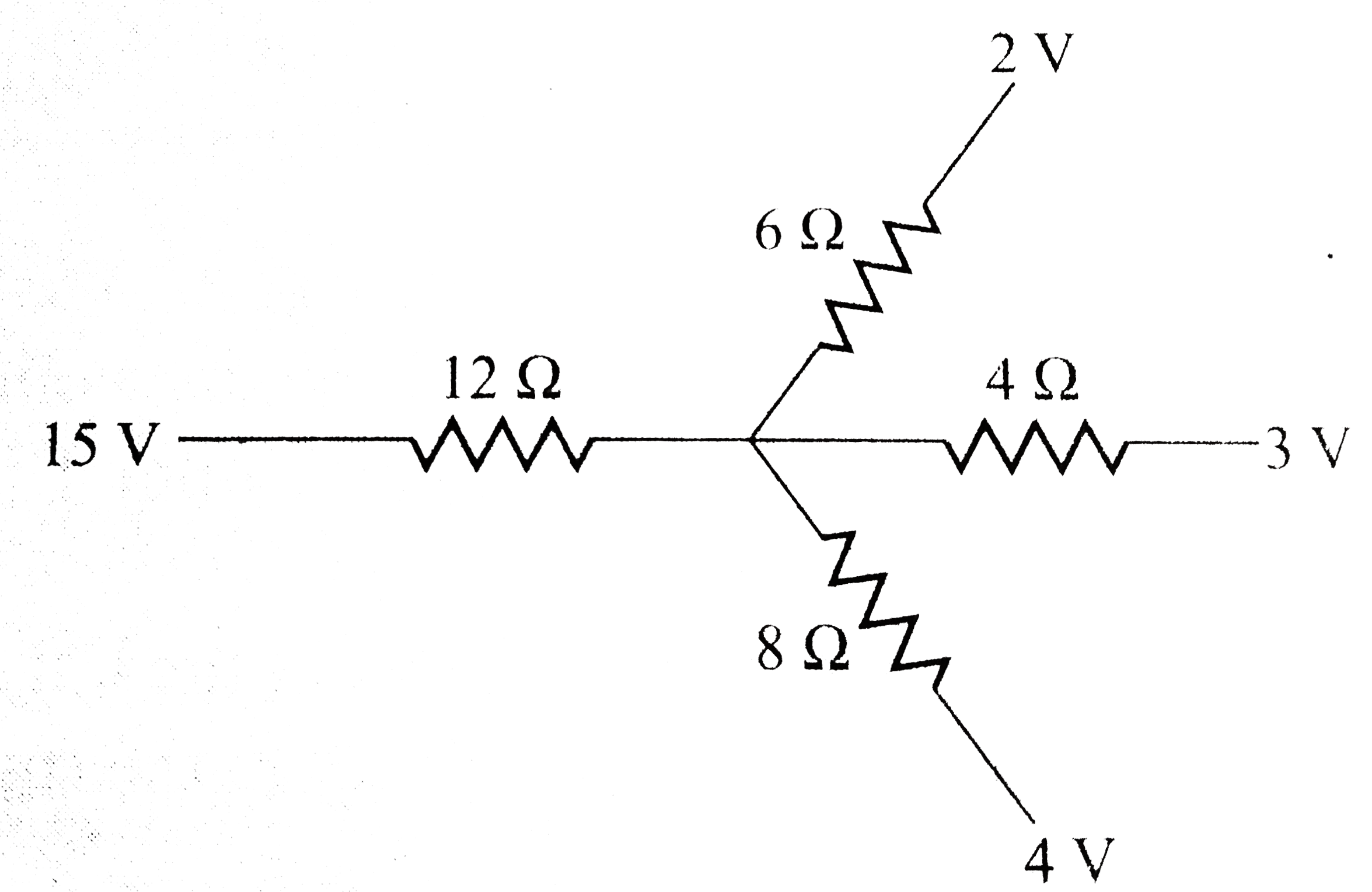
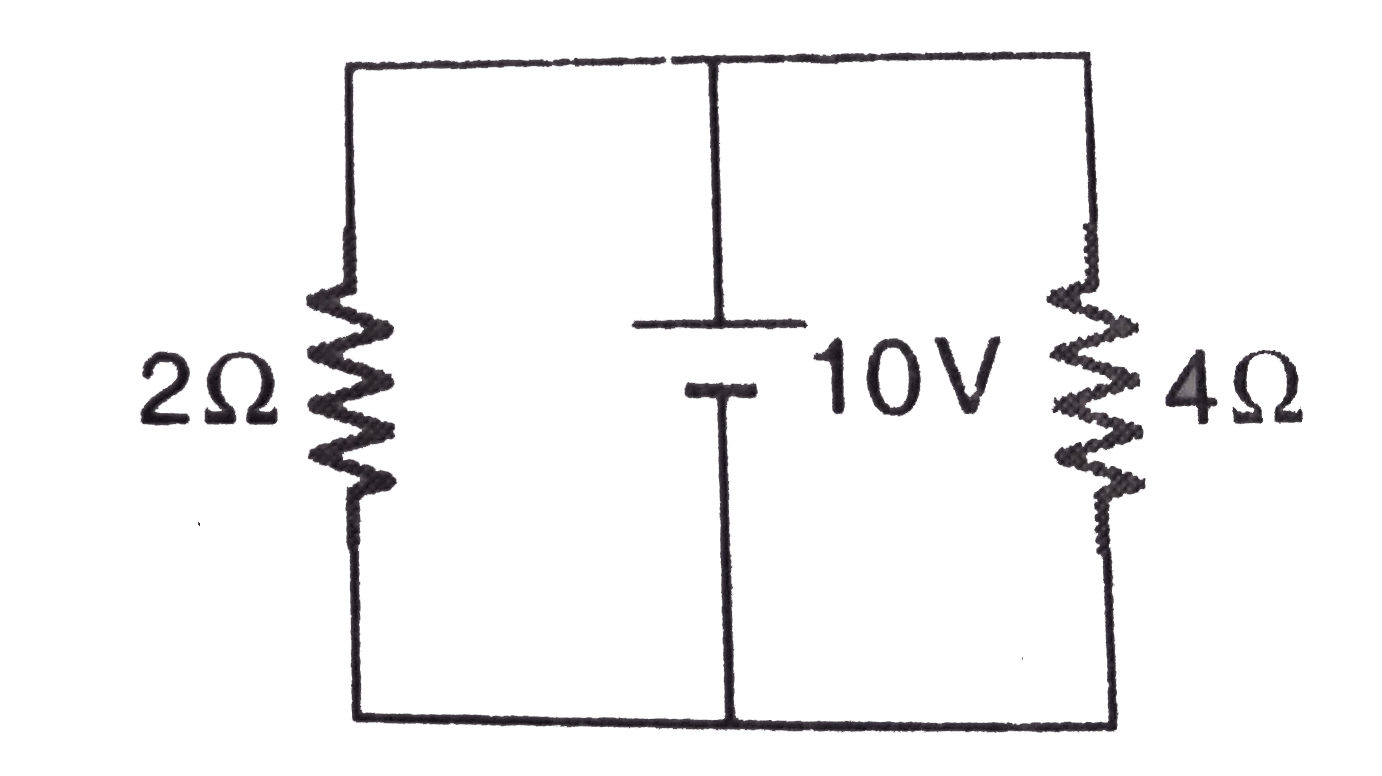
View SolutionFind the current through 2Ω and 4Ω resistance.
View SolutionThe wire star of the previous problem is connected to the circuit at points P and C. Find the equivalent resistance.
View SolutionFind the current through the 10(Ω)resistor shown in figure.

View SolutionFind the current through the 10(Ω)resistor shown in figure.

View SolutionSuppose all the surfaces in the previous problem are rough. The direction of friction on B due to A
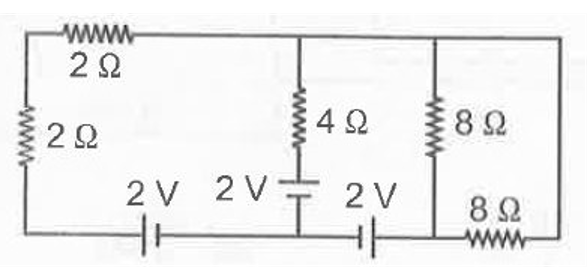
View SolutionFind the current through 4Ω resistor in the circuit shown in figure.
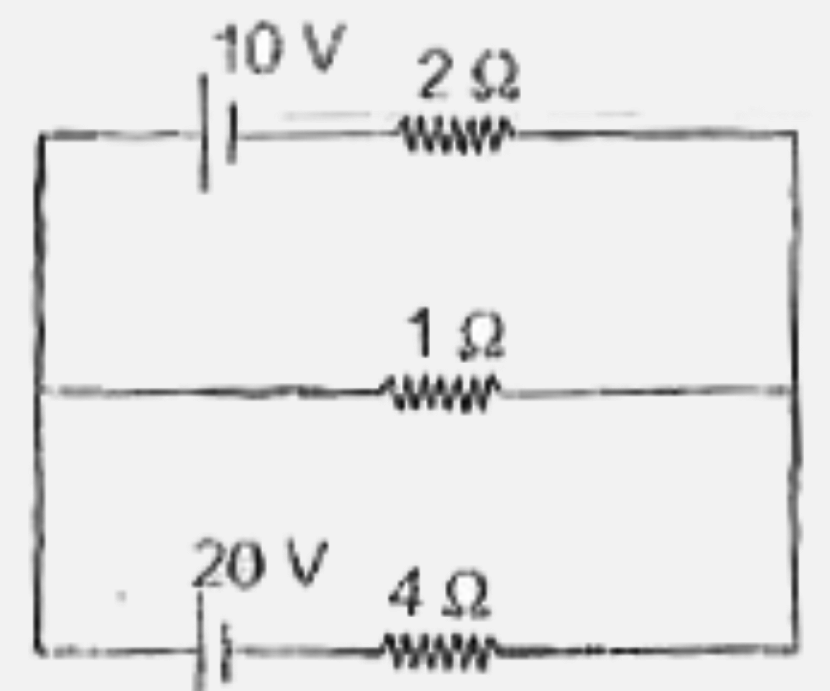
View SolutionThe value of current through 2Ω resistor is
View SolutionIn the circuit diagram shown in find the current through the 1Ω resistor.
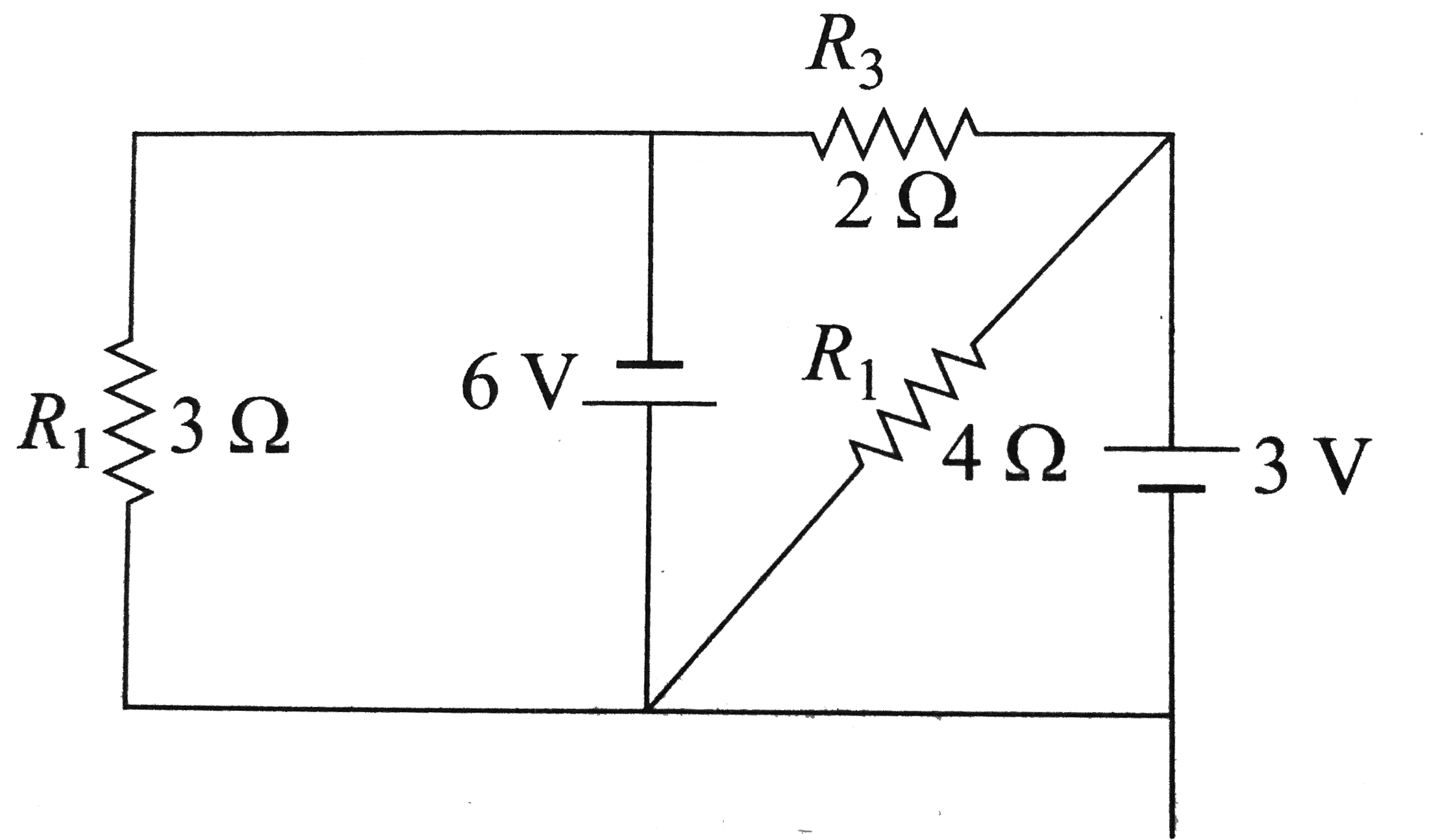
View SolutionIn the diagram find out the current through 2Ω (R3) :
View Solution
