A body starting from rest moves along a straight line with a constant acceleration. The variation of speed (v) with distance (s) is represented by the graph:

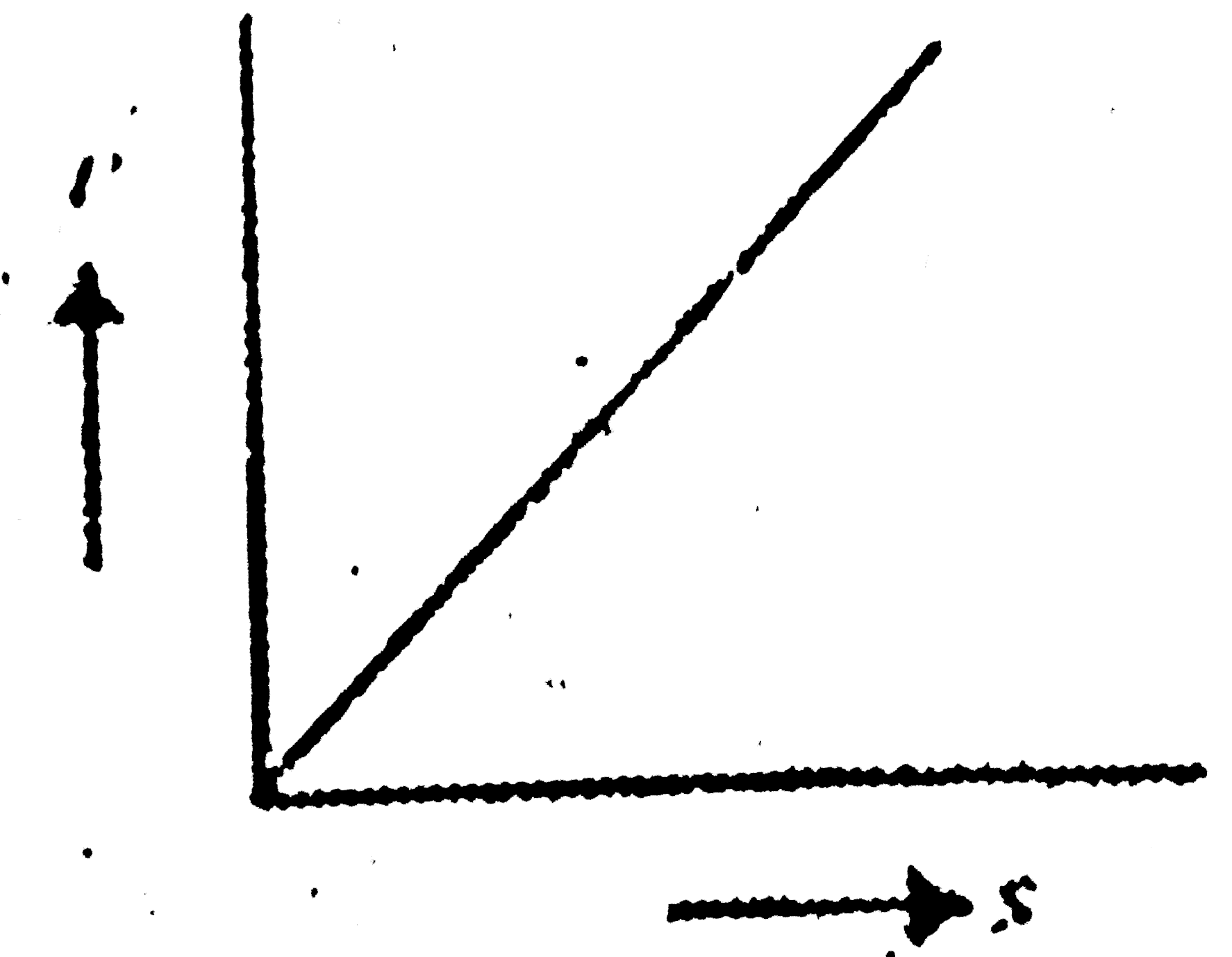

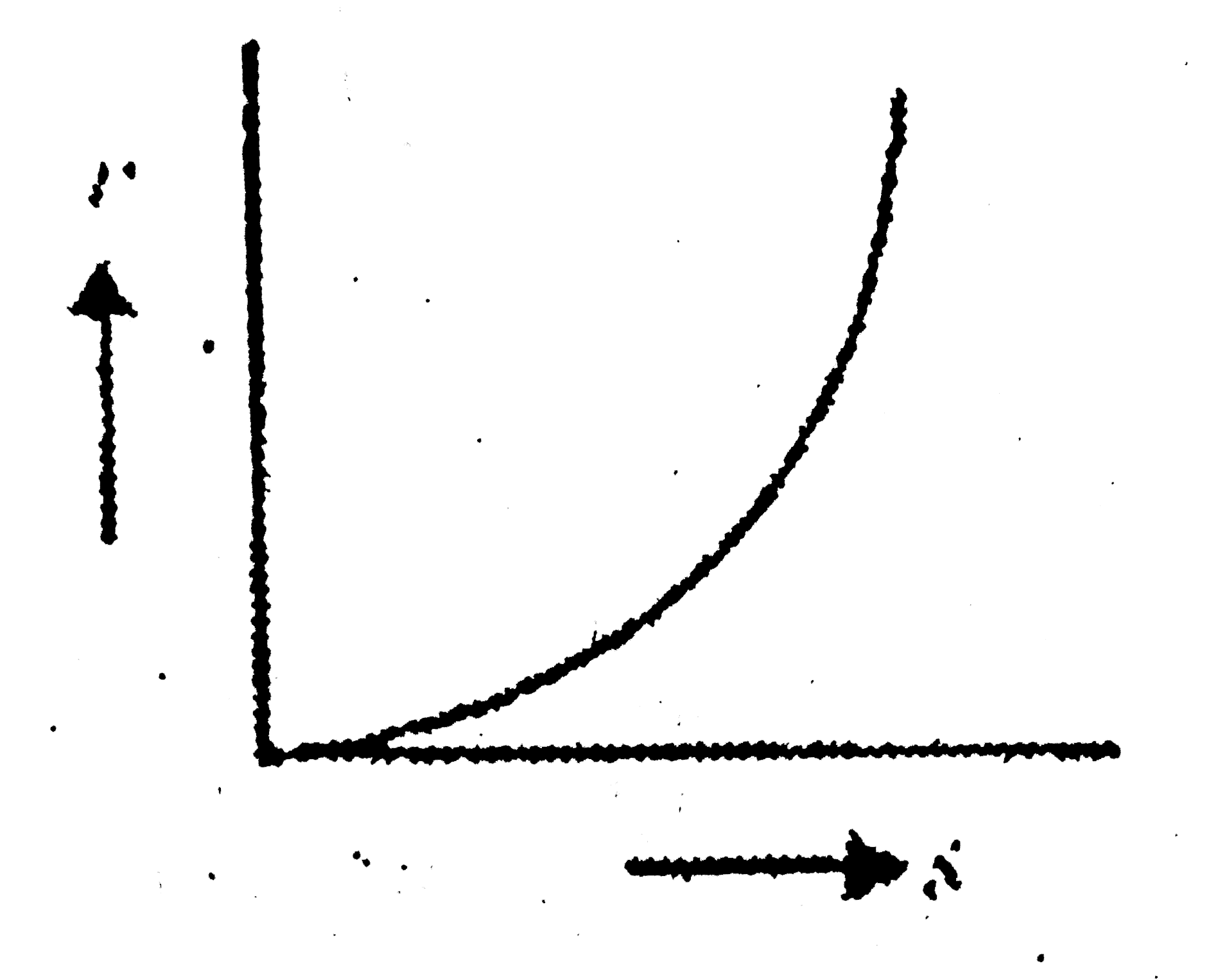
The correct Answer is:B
To solve the problem, we need to analyze the motion of a body starting from rest and moving with constant acceleration. We will use the third equation of motion to relate speed (v) and distance (s).
1. Identify Initial Conditions:
The body starts from rest, which means the initial velocity u=0.
2. Use the Third Equation of Motion:
The third equation of motion states:
v2=u2+2as
Here, v is the final velocity, u is the initial velocity, a is the constant acceleration, and s is the distance traveled.
3. Substitute Initial Velocity:
Since the body starts from rest, we substitute u=0 into the equation:
v2=0+2as
This simplifies to:
v2=2as
4. Rearranging the Equation:
We can rearrange this equation to express v in terms of s:
v=√2as
5. Graphical Representation:
The equation v=√2as indicates that the relationship between v and s is a square root function. If we plot v against s, the graph will be a curve that opens upwards, resembling a parabola.
6. Conclusion:
Thus, the variation of speed v with distance s is represented by a graph that is symmetric to a parabola. The correct option corresponding to this relationship in the provided choices is option 3.
The body starts from rest, which means the initial velocity u=0.
The third equation of motion states:
v2=u2+2as
Here, v is the final velocity, u is the initial velocity, a is the constant acceleration, and s is the distance traveled.
Since the body starts from rest, we substitute u=0 into the equation:
v2=0+2as
This simplifies to:
v2=2as
We can rearrange this equation to express v in terms of s:
v=√2as
The equation v=√2as indicates that the relationship between v and s is a square root function. If we plot v against s, the graph will be a curve that opens upwards, resembling a parabola.
Thus, the variation of speed v with distance s is represented by a graph that is symmetric to a parabola. The correct option corresponding to this relationship in the provided choices is option 3.
Similar Questions
A particle starting from rest moves along a straight line with constant acceleration for this velocity displacement graph will have the form-
View SolutionA particle starting from rest moves in a straight line with acceleration as shown in the a-t graph. Find the distance (in m) travelled by the particle in the first four seconds from start of its motion.
Q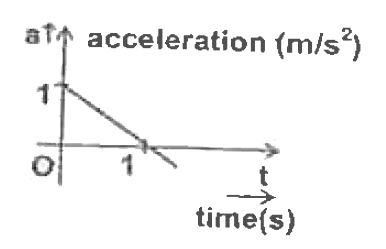
View SolutionA car, starting from rest, moves in a straight line with constant acceleration . 4m/s2 After some time, it immediately starts retarding at constant rate 2m/s2 until it comes to rest. If the car moved for a total time 18 seconds, the total distance covered is
View SolutionA particle starts from rest and moves with constant acceleration. Then velocity displacement curve is:
View SolutionA body starts from rest and moves with constant acceleration. The ratio of distance covered by the body in nth second to that covered in n second is.
View SolutionFor a body moving with uniform acceleration along straight line, the variation of its velocity (v) with position (x) is best represented by
View SolutionA particle at rest starts moving in a horizontal straight line with a uniform acceleration. The ratio of the distances covered during the fourth and third seconds is
View SolutionA particle starts from rest at t=0 and moves in a straight line with an acceleration as shown below. The velocity of the particle at t=3 s is

View SolutionA body with constant acceleration always moves along a straight line.
A body with constant magnitude of acceleration may not speed up.
View SolutionA particle starts motion from rest and moves along a straight line. Its acceleration-time graph is shown. Find out speed of particle at t=2s and at t=3s.

View Solution
