The ratio of thermal conductivity of two rods of different material is 5:4. The two rods of same area of cross-section and same thermal resistance will have the lengths in the ratio
4:5
9:1
1:9
5:4
The correct Answer is:D
To solve the problem, we need to determine the ratio of the lengths of two rods made from different materials, given that their thermal conductivities are in the ratio of 5:4, and they have the same area of cross-section and thermal resistance.
1. Understanding Thermal Resistance:
The thermal resistance (R) of a rod is given by the formula:
R=ρLA
where:
- R is the thermal resistance,
- ρ is the resistivity (which is inversely related to thermal conductivity k),
- L is the length of the rod,
- A is the area of cross-section.
2. Given Ratios:
We know:
- The ratio of thermal conductivities k1:k2=5:4.
- The area of cross-section for both rods is the same, so A1=A2.
3. Relating Resistivity and Conductivity:
Since resistivity ρ is inversely related to thermal conductivity k, we can express the ratio of resistivities as:
ρ1ρ2=k2k1=45
4. Setting Up the Resistance Equations:
The thermal resistances for the two rods can be expressed as:
R1=ρ1L1A1andR2=ρ2L2A2
Since A1=A2, we can denote A as the common area:
R1=ρ1L1AandR2=ρ2L2A
5. Equating Thermal Resistances:
Given that the thermal resistances are equal (R1=R2):
ρ1L1A=ρ2L2A
Simplifying this gives:
ρ1L1=ρ2L2
6. Substituting the Resistivity Ratio:
Substitute ρ1=45ρ2 into the equation:
(45ρ2)L1=ρ2L2
Dividing both sides by ρ2 (assuming ρ2≠0):
45L1=L2
7. Finding the Length Ratio:
Rearranging gives:
L1=54L2
Therefore, the ratio of lengths L1:L2 is:
L1:L2=5:4
Final Answer:
The ratio of the lengths of the two rods is 5:4.
The thermal resistance (R) of a rod is given by the formula:
R=ρLA
where:
- R is the thermal resistance,
- ρ is the resistivity (which is inversely related to thermal conductivity k),
- L is the length of the rod,
- A is the area of cross-section.
We know:
- The ratio of thermal conductivities k1:k2=5:4.
- The area of cross-section for both rods is the same, so A1=A2.
Since resistivity ρ is inversely related to thermal conductivity k, we can express the ratio of resistivities as:
ρ1ρ2=k2k1=45
The thermal resistances for the two rods can be expressed as:
R1=ρ1L1A1andR2=ρ2L2A2
Since A1=A2, we can denote A as the common area:
R1=ρ1L1AandR2=ρ2L2A
Given that the thermal resistances are equal (R1=R2):
ρ1L1A=ρ2L2A
Simplifying this gives:
ρ1L1=ρ2L2
Substitute ρ1=45ρ2 into the equation:
(45ρ2)L1=ρ2L2
Dividing both sides by ρ2 (assuming ρ2≠0):
45L1=L2
Rearranging gives:
L1=54L2
Therefore, the ratio of lengths L1:L2 is:
L1:L2=5:4
The ratio of the lengths of the two rods is 5:4.
Similar Questions
The ratio of the thermal conductivities of two different materials is 1:2. The thermal resistance of the rods of these materials having the same thickness are equal. Find the ratio of the length of rods.
View SolutionThe ratio of thermal conductivites of two different metals is 5:3. In order to have the same thermal resistance in these metals of equal thickness what should be the ratio of their length?
View Solution
Knowledge Check
Two rods of length l1andl2 and coefficients of thermal conductivities k1andK2 are kept touching each other. Both have the same area of cross-section. The equivalent of thermal conductivity is
AK1+K2BK1l1+K2l2CK1l1+K2l2l1+l2Dl1+l2(l1/K1)+(l2/K2)
The end of two rods of different materials with their thermal conductivities, area of cross-section and lengths all in the ratio 1:2 are maintained at the same temperature difference. If the rate of flow of heat in the first rod is 4cal/s. Then, in the second rod rate of heat flow in cal/s will be
View SolutionThe ratio of the areas of cross section of two rods of different materials is 1:2 and the ratio of ther themal conductivities of their mateirals is 4: 3. On keeping equal temperature difference between the ends of theserods, the rate of conduction of heat are equal. The ratio of the lengths of the rods is
View SolutionTwo wires of the same materical having equal area of cross-section have L and 2L. Their respective resistances are in the ratio
View Solution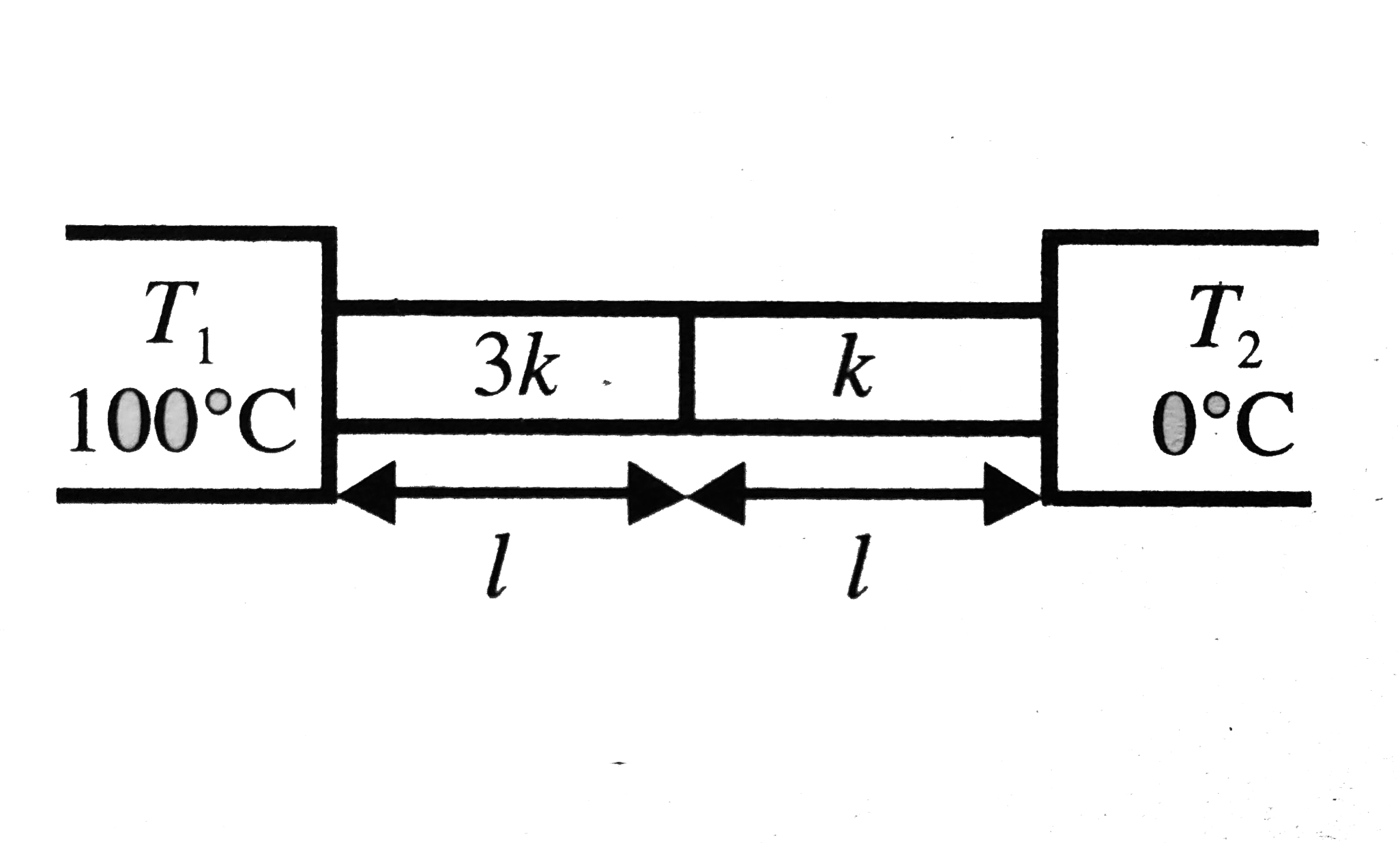
Two rods A and B of same length and cross-sectional area are connected in series and a temperature difference of 100∘C is maintained across the combination as shoen in Fig. If the thermal conductivity of the rod A is 3 k and that of rod B is k, Then
i.Determine the thermal resistance of each rod.
ii. determine the heat current flowing through each rod.
iii. determine the heat current flowing through each rod.
iv. plot the variation of temperature along the length of the rod.
View SolutionThe ratio of the diameters of two metallic rods of the same material is 2:1 and their lengths are in the ratio 1:4. If the temperature difference between their ends are equal, the rate of flow of heat in them will be in the ratio
View SolutionA slab consists of two layers of different materials of the same thickness and having thermal conductivities K1 and K2. The equivalent thermal conductivity of the slab is
View Solution
Statement I: Two solid cylindrical rods of identical size and different thermal conductivity K1 and K2 are connected in series. Then the equivalent thermal conductivity of two rods system is less than that value of thermal conductivity of either rod.
Statement II: For two cylindrical rods of identical size and different thermal conductivity K1 and K2 connected in series, the equivalent thermal conductivity K is given by 2K=1K1+1K2
View Solution
