
A and B are tqo isolated spheres kept in close proximity so that they can exchange energy by radiation. The two spheres have identical physical dimensions but the surface of A behaves like a perfactly black body while the surface of B reflects of all the radiations it receives. They are isolated from all other sources of radiation.
(a)If they are in thermal equilibrium and exchange equal amounts of radiation per second then they will be at same absolute temperature, .
(b)If they are in thermal equilibrium and exchange equal amounts of radiation per second then .
(c)If they are not in thermal equilibrium and are each at at the same temperature , then the sphere A will lose thermal energy and B will gain thermal energy.
(d)If they are not in thrmal equilibrium and are each at at the same temperature , Then the sphere A will gain thermal energy and B will lose thermal energy.
The correct Answer is:A
Since they are in thermal equilibrium the temperatures must necessarily be equal. Temperature equality is a necessary and sufficient condition for thermal equilibrium (zeroth law of thermodynamics).
Topper's Solved these Questions
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Multiple Correct
25 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Comprehension
30 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Subjective
25 Videos
- BASIC MATHEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - BASIC MATHEMATICSEXERCISE - Exercise 2.6
20 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - INTEGER_TYPE
1 Videos
Similar Questions
(i) Two isolated metal spheres A and B have radii R and 2R respectively and same charge q. Find which of the two spheres have
(a) greater capacitance
(b) greater energy density just outside the surface of the spheres.
(ii) (a) Show that the equipotential surfaces are closed together in the regions of strong field and far apart in the region of weak field. Draw equipotential surfaces for an electric dipole.
(b) Concentric equipotential surfaces due to a charged body placed at the centre are shown. Identify the polarity of the charge and draw the electric field lines due to it.
View SolutionTwo identical conduction spheres, one having an initial charge +Q and the other initially uncharged, are brought into contact.
(a) What is the new charge on each sphere?
(b) While the spheres are in contact, a positively chaged rod is moved close to one sphere, causing a redistribution of hte charges on the two spheres so the charge on hte sphere closest to the rod has a charge-Q. What is the charge to the other sphere?
View Solution
Knowledge Check
This passage is adapted from Daniel Chamovitz, What a Plant Knows: A Field Guide to the Senses. ©2012 by Daniel Chamovitz.
The Venus flytrap [Dionaea muscipula] needs to know when an ideal meal is crawling across its leaves. Closing its trap requires a huge expense of energy, and reopening the trap can take several hours, so Dionaea only wants to spring closed when it’s sure that the dawdling insect visiting its surface is large enough to be worth its time. The large black hairs on their lobes allow the Venus flytraps to literally feel their prey, and they act as triggers that spring the trap closed when the proper prey makes its way across the trap. If the insect touches just one hair, the trap will not spring shut, but a large enough bug will likely touch two hairs within about twenty seconds, and that signal springs the Venus flytrap into action.
We can look at this system as analogous to short-term memory. First, the flytrap encodes the information (forms the memory) that something (it doesn’t know what) has touched one of its hairs. Then it stores this information for a number of seconds (retains the memory) and finally retrieves this information (recalls the memory) once a second hair is touched. If a small ant takes a while to get from one hair to the next, the trap will have forgotten the first touch by the time the ant brushes up against the next hair. In other words, it loses the storage of the information, doesn’t close, and the ant happily meanders on. How does the plant encode and store the information from the unassuming bug’s encounter with the first hair? How does it remember the first touch in order to react upon the second?
Scientists have been puzzled by these questions ever since John Burdon-Sanderson’s early report on the physiology of the Venus flytrap in 1882. A century later, Dieter Hodick and Andreas Sievers at the University of Bonn in Germany proposed that the flytrap stored information regarding how many hairs have been touched in the electric charge of its leaf. Their model is quite elegant in its simplicity. In their studies, they discovered that touching a trigger hair on the Venus flytrap causes an electric action potential [a temporary reversal in the electrical polarity of a cell membrane] that induces calcium channels to open in the trap (this coupling of action potentials and the opening of calcium channels is similar to the processes that occur during communication between human neurons), thus causing a rapid increase in the concentration of calcium ions.
They proposed that the trap requires a relatively high concentration of calcium in order to close and that a single action potential from just one trigger hair being touched does not reach this level. Therefore, a second hair needs to be stimulated to push the calcium concentration over this threshold and spring the trap. The encoding of the information requires maintaining a high enough level of calcium so that a second increase (triggered by touching the second hair) pushes the total concentration of calcium over the threshold. As the calcium ion concentrations dissipate over time, if the second touch and potential don’t happen quickly, the final concentration after the second trigger won’t be high enough to close the trap, and the memory is lost.
Subsequent research supports this model. Alexander Volkov and his colleagues at Oakwood University in Alabama first demonstrated that it is indeed electricity that causes the Venus flytrap to close. To test the model they rigged up very fine electrodes and applied an electrical current to the open lobes of the trap. This made the trap close without any direct touch to its trigger hairs (while they didn’t measure calcium levels, the current likely led to increases). When they modified this experiment by altering the amount of electrical current, Volkov could determine the exact electrical charge needed for the trap to close. As long as fourteen microcoulombs—a tiny bit more than the static electricity generated by rubbing two balloons together—flowed between the two electrodes, the trap closed. This could come as one large burst or as a series of smaller charges within twenty seconds. If it took longer than twenty seconds to accumulate the total charge, the trap would remain open.
Which choice provides the best evidence for the answer to the previous question?ALines 3-7 (“Closing . . . time”)BLines 7-11 (“The large . . . across the trap”)CLines 11-14 (“If the . . . action”)DLines 16-18 (“First . . . hairs”)
In a hexaonal system system of cycstals, a frequently encountered arrangement of atoms is described as a hexagonal prism. Here, the top and bottom of the cell are refular hexagons, and three atoms are sandwiched in between them. A space-cilling model of this structure, called hexagonal close-paked is constituted of a sphere on a flat surface surrounded in the same plane by six identical spheres as closely as possible. Three spherres are then placed overt the first layer so that they toych each other and represent the second layer so that they toych each other and present the second layer. Each one of the three spheres touches three spheres of the bottom layer. Finally, the second layer is convered with a third layer identical to the bottom layer in relative position. Assume the radius of every sphere to be r.
The empty space in this hcp unit cell is
(a)74%
(b)48.6%
(c)32%
(d)26%
View SolutionEinstein in 1905 proppunded the special theory of relativity and in 1915 proposed the general theory of relativity. The special theory deals with inertial frames of reference. The general theory of relativity deals with problems in which one frame of reference. He assumed that fixed frame is accelerated w.r.t. another frame of reference of reference cannot be located. Postulated of special theory of realtivity
● The laws of physics have the same form in all inertial systems.
● The velocity light in empty space is a unicersal constant the same for all observers.
● Einstein proved the following facts based on his theory of special relativity. Let v be the velocity of the speceship w.r.t a given frame of reference. The obserations are made by an observer in that reference frame.
● All clocks on the spaceship wil go slow by a factor √1−v2/c2
● All objects on the spaceship will have contracted in length by a factor √1−v2/c2
● The mass of the spaceship increases by a factor √1−v2/c2
● Mass and energy are interconvertable E=mc2
The speed of a meterial object can never exceed the velocity of light.
● If two objects A and B are moving with velocity u and v w.r.t each other along the x-axis, the relative velocity of A w.r.t. B=u−v1−uv/v2
A stationary body explodes into two fragments each of rest mass 1kg that move apart at speed of 0.6c relative to the original body. The rest mass of the original body is -
View SolutionTwo bodies A and B having equal surface areas are maintained at temperatures 10∘C . And 20∘C . The thermal radiation emitted in a given time by A and B are in the ratio
View SolutionAssuming the sun to have a spherical outer surface of radius r radiating like a black body at temperature t∘C. The power received by a unit surface (normal to the incident rays) at a distance R from the centre of the sun is
where σ is the Stefan's constant.
View SolutionTwo metallic spheres S1andS2 are made of the same material and have got identical surface finish. The mass of S1 is thrice that of S2. Both the spheres are heated to the same high temperature and placed in the same room having lower temperature but are thermally insulated from each other. the ratio of the initial rate of cooling of S1 to that of S2 is
(a)13(b)1√3(c)√31(d)(13)13
View SolutionThe force of interaction between the molecules of same substance is called cohesive force hile force of interaction between molecules of different substances is called adhesive force . Both the forces are attracive and have a range of about 10 A . If we consider a molecule . A well inside a liquid we find that it is equally attracted by the surrounding molecules in all the directions ( with a sphere of radius 10 Å ) and so it does not experience any resultant force . On or near the surface of a liquid , the molecules do not exist on the free side and so a molecule ( say B ) experiences a resultant force vertically downwards into the liquid . For this reason , the molecules of the surface have a tendency to go into the liquid . Thus , the surface tends to contract and gives rise to surface tension .
As surface molecules like B experience a net downward force of cohension and have tendency to go down , so in increasing the area of the surface more molecules are to be shifted to the surface from inside . Thus , more mechnical work will have to be done against the net downward force of cohension . This work is stored by the molecules in the surfaces as potential energy called free surface energy .
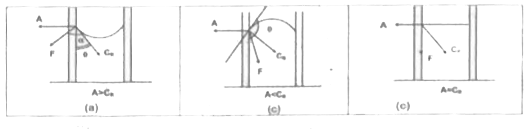
Furthermore , molcules like P , in contact with the liquid will stick to the solid surface , i.e will meet it if the force of adhesion A is greater than net force of cohension C . The liquid will not the solid surface if C>A
Also , molecules like Q at the surface in contact with the solid will experience a net force of cohension CR . If adhesion A is greater then cohension CR , the resultant force will be F . As the liquid can't support tangential force , F must be perpendicular to the surface of the liquid . So , the menisus will be concave and the angle of contact will be acute (>90∘) . However , if adhesion is lesser than cohension , the resultant force F will be directed into the liquid and so the menisus ( which is perpendicular to F as liquid support tangential force ) will be convex and the angle of contact will be obtuse (>90∘)
A liquid particle B , which is present in the vicinity particle A can exert a force on A if the distance of B from A is
View SolutionThe force of interaction between the molecules of same substance is called cohesive force hile force of interaction between molecules of different substances is called adhesive force . Both the forces are attracive and have a range of about 10 A . If we consider a molecule . A well inside a liquid we find that it is equally attracted by the surrounding molecules in all the dirctions ( with a sphere of radius 10 Å ) and so it does not experience any resultant force . On or near the surface of a liquid , the molecules do not exist on the free side and so a molecule ( say B ) experiences a resultant force vertically downwards into the liquid . For this reason , the molecules of the surface have a tendency to go into the liquid . Thus , the surface tends to contract and gives rise to surface tension .
As surface molecules like B experience a net downward force of cohension and have tendency to go down , so in increasing the area of the surface more molecules are to be shifted to the surface from inside . Thus , more mechnical work will have to be done against the net downward force of cohension . This work is stored by the molecules in the surfaces as potential energy called free surface energy .
Furthermore , molcules like P , in contact with the liquid will stick to the solid surface , i.e will meet it if the force of adhesion A is greater than net force of cohension C . The liquid will not the solid surface if C>A
Also , molecules like Q at the surface in contact with the solid will experience a net force of cohension CR . If adhesion A is greater then cohension CR , the resultant force will be F . As the liquid can't support tangential force , F must be perpendicular to the surface of the liquid . So , the menisus will be concave and the angle of contact will be acute (>90∘) . However , if adhesion is lesser than cohension , the resultant force F will be directed into the liquid and so the menisus ( which is perpendicular to F as liquid support tangential force ) will be convex and the angle of contact will be obtuse (>90∘)

The free suface energy , stored in the surface is because of work done
View Solution
