A thin copper rod of uniform cross section A square metres and of length L metres has a spherical metal sphere of radius r metre at Its one end symmetrically attached to the copper rod. The thermal conductivity of copper is K and the emissivity of the spherical surface of the sphere is ε.The free end of the copper rod is maintained at the temperature T kelvin by supplying thermal energy from a P watt source. Steady state conditions are allowed to be established while the rod is properly insulated against heat loss from its lateral surface. Surroundings are at 0∘C Stefan's constant=σW/m2K4.
After the steady state conditions are reached,the temperature of the spherical end of the rod, TS is
A.TS=T−PLKA
B.TS=0∘C
C.TS=PLKA
D.TS=T−P(L+r)KA
The correct Answer is:D

The distance from the end A of the copper rod (where power is supplied) and centre O of the metal sphere is (L+r). Hence , in the steady state condions,
P=KA(T−TS)L+r
Which gives TS=T−P(L+r)KA
(The heat is trainsmitted up to centre of the spherical end and the sphere loses energy by radiation out of its spherical surface.)
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Integer8videos
CALORIMETRY
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Solved Example13videos
CALORIMETRY
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Multiple Correct25videos
CALORIMETRY
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - BASIC MATHEMATICSEXERCISE - Exercise 2.620videos
BASIC MATHEMATICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - INTEGER_TYPE1videos
CENTRE OF MASS
Similar Questions
A thin copper rod of uniform cross section A square metres and of length L metres has a spherical metal sphere of radius r metre at tis one end symmetrically attached to the copper rod. The thermal conductivity of copper is K and the emissivity of the spherical surface of the sphere is ε.The free end of the copper rod is maintained at the temperature T kelving by supplying thermal energy from a P watt source. Steady state conditions are allowed ot be established while the rod is properly insulated aginst heat loss from its lateral surface. Surroundings are at 0∘C Stefan's constant=σW/m2K4.
If the metal sphere attached at the end of the copper rod is made of brass, whose thermal conductivity is Kb<K, then which of the following statements is true?View SolutionA thin copper rod of uniform cross section A square metres and of length L metres has a spherical metal sphere of radius r metre at tis one end symmetrically attached to the copper rod. The thermal conductivity of copper is K and the emissivity of the spherical surface of the sphere is ε.The free end of the copper rod is maintained at the temperature T kelving by supplying thermal energy from a P watt source. Steady state conditions are allowed ot be established while the rod is properly insulated aginst heat loss from its lateral surface. Surroundings are at 0∘C Stefan's constant=σW/m2K4.
The net power that will be radiated out, PS from the sphere after steady state condition are reached isView SolutionThe ends of copper rod of length 1m and area of cross section 1cm2 are maintained at 0∘C and 100∘C. At the centre of rod, there is a source of heat of 32W. The thermal conductivity of copper is 400W/mK
 View Solution
View SolutionThe ends of a rod of uniform thermal conductivity are maintained at different (constant) temperatures. Afer the steady state is achieved:
View SolutionA uniform copper rod 50 cm long is insulated on the sides, and has its ends exposedto ice and steam,respectively. If there is a layer of water 1 mm thick at each end, calculate the temperature gradient in the bar. The thermal conductivity of copper is 436Wm−1K−1 and that of water is 0.436Wm−1K−1.
View Solution
Two ends of a rod of uniform cross sectional area are kept at temperature 3T0 and T0 as shown. Thermal conductivity of rod varies as k=αT, (where α is a constant and T is absolute temperature). In steady state, the temperature of the middle section of the rod isView SolutionThe area of cross-section of rod is given by A=A0(1+αx) where A0 & α are constant and x is the distance from one end. If the thermal conductivity of the material is K. What is the thermal resistancy of the rod if its length is l0?
View SolutionA copper rod of cross sectional area A carries a uniform current I through it. At temperature T if the volume charge density of the rod is ρ how long will the charges take to travel a distance d?
View SolutionA uniform rod ofmass M and length L is hanging from its one end free to rotate in a veritcal plane.A small ball of equal mass is attached of the lowe end as shown. Time period of small oscillations of the rod is
 View Solution
View Solution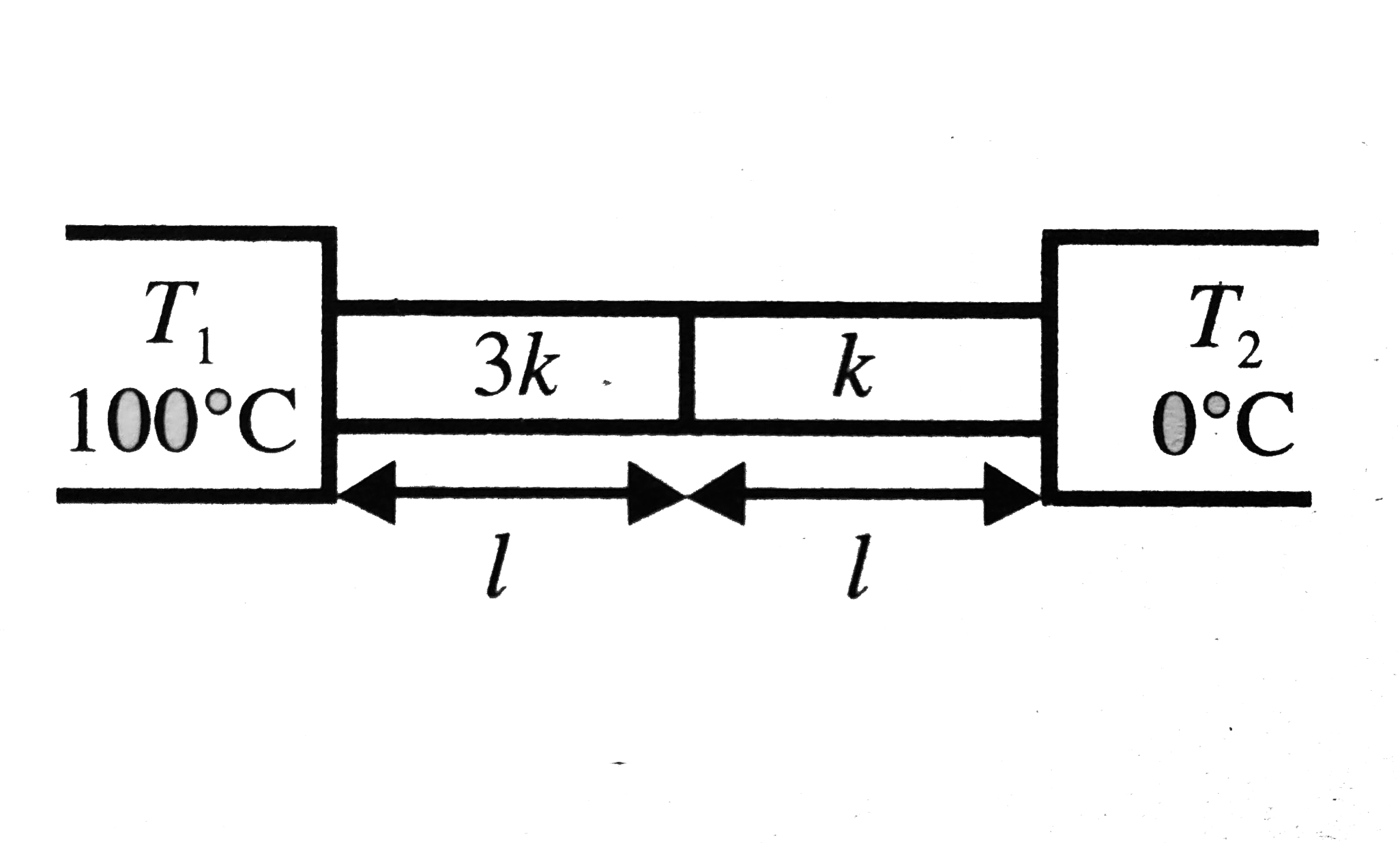
Two rods A and B of same length and cross-sectional area are connected in series and a temperature difference of 100∘C is maintained across the combination as shoen in Fig. If the thermal conductivity of the rod A is 3 k and that of rod B is k, Then
i.Determine the thermal resistance of each rod.
ii. determine the heat current flowing through each rod.
iii. determine the heat current flowing through each rod.
iv. plot the variation of temperature along the length of the rod.View Solution

