The ends of a rod of uniform thermal conductivity are maintained at different (constant) temperatures. Afer the steady state is achieved:
heat flows in the rod from high temperature to low temperature even if the rod has the non-unform cross sectional area
temperature gradient along length is same even if the rod has the non-unform cross sectional area
heat current is same even if the rod hasnon-unform cross sectional area
If the rod has uniform cross-sectional area the temperature is same all the point at rod.
The correct Answer is:A, C
To solve the problem regarding the heat conduction in a rod of uniform thermal conductivity maintained at different constant temperatures, we can break it down into the following steps:
Step 1: Understand the Setup
We have a rod with two ends maintained at different constant temperatures, TH (hot end) and TC (cold end). The rod has uniform thermal conductivity k.
Hint: Identify the temperatures at both ends of the rod and recognize that steady state means a constant temperature distribution along the rod.
Step 2: Define Steady State
In steady state, the temperature at each point along the rod does not change over time. This means that while heat is flowing from the hot end to the cold end, the temperature at the hot end remains TH and the temperature at the cold end remains TC.
Hint: Remember that steady state implies a constant temperature distribution, not thermal equilibrium.
Step 3: Apply Fourier's Law of Heat Conduction
According to Fourier's law, the heat transfer Q through the rod can be expressed as:
Q=k⋅A⋅TH−TCL
where A is the cross-sectional area of the rod, and L is the length of the rod.
Hint: Recognize that heat flows from the higher temperature to the lower temperature.
Step 4: Analyze Heat Flow
Heat will always flow from the hot end to the cold end, regardless of whether the rod has a uniform or non-uniform cross-sectional area. Therefore, the first statement that heat flows from high temperature to low temperature is correct.
Hint: Focus on the direction of heat flow and the implications of temperature differences.
Step 5: Temperature Gradient
The temperature gradient dTdx is defined as:
dTdx=TH−TCL
If the rod has a non-uniform cross-sectional area, the temperature gradient will not remain constant because it is inversely proportional to the cross-sectional area. Thus, the second statement is incorrect.
Hint: Consider how changes in cross-sectional area affect the temperature gradient.
Step 6: Heat Current Consistency
The heat current (rate of heat transfer) remains constant throughout the rod in steady state, even if the cross-sectional area varies. This is due to the conservation of energy, which states that the amount of heat entering one end of the rod must equal the amount of heat leaving the other end.
Hint: Think about the principle of conservation of energy in the context of heat flow.
Step 7: Temperature Uniformity
At steady state, the temperature will not be the same at all points along the rod if there is heat flow. Therefore, the fourth statement is incorrect.
Hint: Remember that heat flow implies a temperature gradient, which means temperatures will vary along the length of the rod.
Conclusion
Based on the analysis:
- The correct options are 1 (heat flows from high to low temperature) and 3 (heat current is the same throughout the rod).
- The incorrect options are 2 (temperature gradient remains the same) and 4 (temperature is the same at all points).
Final Answer: The correct options are 1 and 3.
---
We have a rod with two ends maintained at different constant temperatures, TH (hot end) and TC (cold end). The rod has uniform thermal conductivity k.
In steady state, the temperature at each point along the rod does not change over time. This means that while heat is flowing from the hot end to the cold end, the temperature at the hot end remains TH and the temperature at the cold end remains TC.
According to Fourier's law, the heat transfer Q through the rod can be expressed as:
Q=k⋅A⋅TH−TCL
where A is the cross-sectional area of the rod, and L is the length of the rod.
Heat will always flow from the hot end to the cold end, regardless of whether the rod has a uniform or non-uniform cross-sectional area. Therefore, the first statement that heat flows from high temperature to low temperature is correct.
The temperature gradient dTdx is defined as:
dTdx=TH−TCL
If the rod has a non-uniform cross-sectional area, the temperature gradient will not remain constant because it is inversely proportional to the cross-sectional area. Thus, the second statement is incorrect.
The heat current (rate of heat transfer) remains constant throughout the rod in steady state, even if the cross-sectional area varies. This is due to the conservation of energy, which states that the amount of heat entering one end of the rod must equal the amount of heat leaving the other end.
At steady state, the temperature will not be the same at all points along the rod if there is heat flow. Therefore, the fourth statement is incorrect.
Based on the analysis:
- The correct options are 1 (heat flows from high to low temperature) and 3 (heat current is the same throughout the rod).
- The incorrect options are 2 (temperature gradient remains the same) and 4 (temperature is the same at all points).
Topper's Solved these Questions
- TRANSMISSION OF HEATBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRANSMISSION OF HEATEXERCISE - Comprehension type
4 Videos
- TRANSMISSION OF HEATBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRANSMISSION OF HEATEXERCISE - Fill in the blanks type
6 Videos
- TRANSMISSION OF HEATBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRANSMISSION OF HEATEXERCISE - Single correct
9 Videos
- THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - 24
1 Videos
- TRAVELLING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Integer
9 Videos
Similar Questions
The two ends of a uniform rod of thermal conductivity k are maintained at different but constant temperatures. The temperature gradientat any point on the rod is dθdl(equal to the difference in temperature per unit length). The heat flow per unit time per unit cross-section of the rod is l then which of the following statements is/are correct:
View SolutionThe thermal conductivity of a rod depends on
View SolutionThe thermal conductivity of a rod depends on
View SolutionThe thermal conductivity of a rod depends on
View SolutionOne end of the rod of length l, thermal conductivity K and area of cross-section A is maintained at a constant temperature of 100∘C. At the other end large quantity of ice is kept at 0∘C . Due to temperature difference, heat flows from left end to right end of the rod. Due to this heat ice will start melting. Neglecting the radiation losses find the expression of rate of melting of ice.
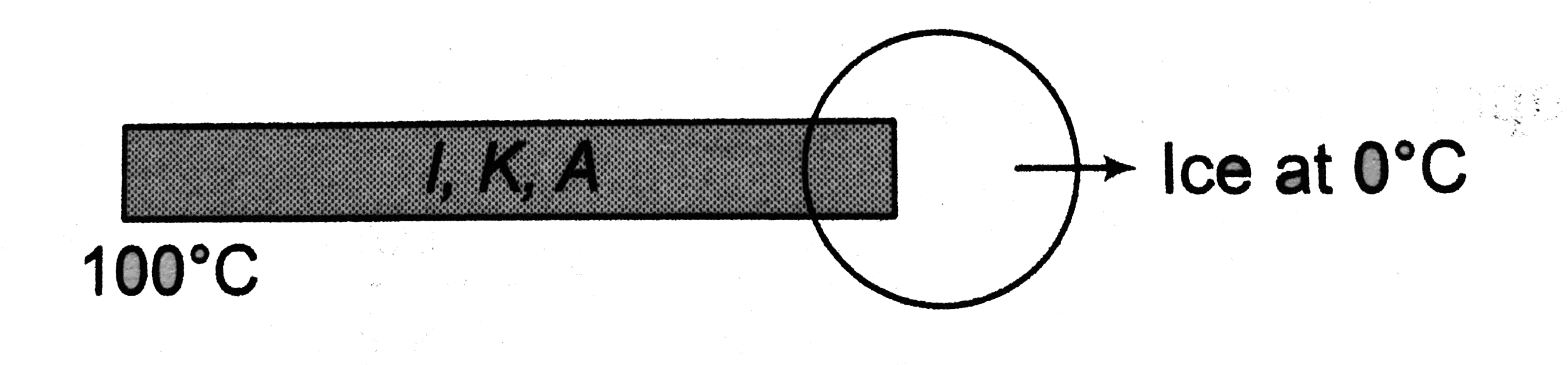 .
.
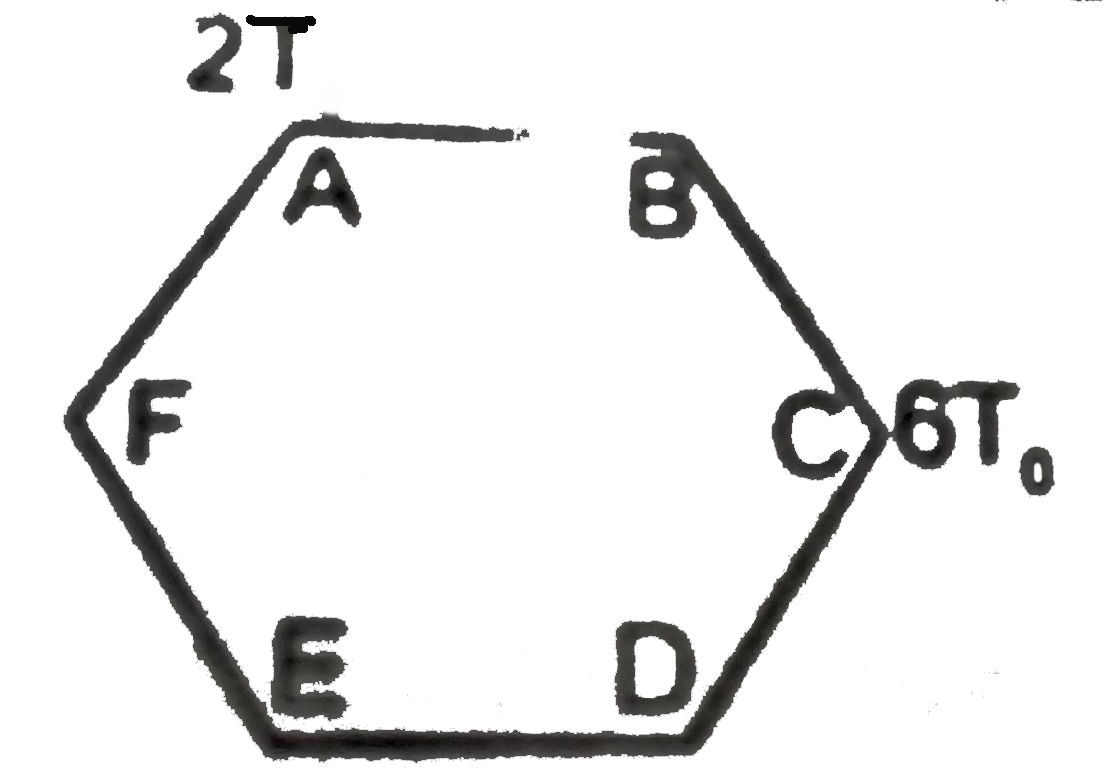
View SolutionSix identical uniform conducting rods are fixed to make a regular hexagon as shown. The ends A and C are maintained at constant temperature 2T0 and 6T0. After the steady state is reached. Pick up the correct relation between temperatures TB,TB,TE and TF of ends B,D,E and F respectively.
View SolutionThree rods of same dimensions have thermal conductivity 3K,2K and K They are arranged as shown in Then the temperature of the junction in steady state is
 .
.
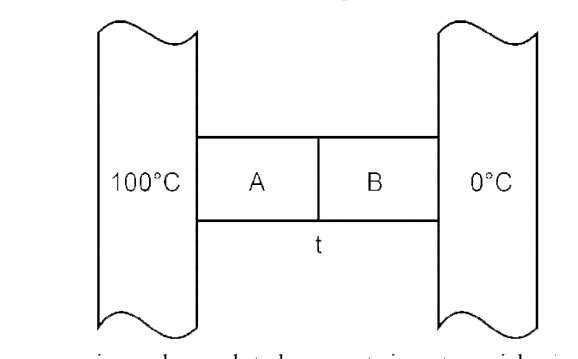
View SolutionTwo metal cubes A and B of same size are arranged as shown in Figure. The extreme ends of the combination are maintained at the indicated temperatures. The arrangement is thermally insulated. The coefficients of thermal conductivity of A and B are 300W/m∘Cand200W/m∘C, respectively. After steady state is reached the temperature t of the interface will be ......
View SolutionA cylinder of radius r made of a material of thermal conductivity K1 is surrounded by a cylindrical shell of inner radius r and outer radius 2r made of a material of thermal conductivity K2. The two ends of the combined system are maintained at two different temperatures. There is no loss of heat across the cylindrical surface and the system is in steady state. Show that the effective thermal conductivity of the system is (K1+3K2)/4.
View SolutionA cylinder of radius R made of a material of thermal conductivity K1 is surrounded by a cylindrical shell of inner radius R and outer radius 2R made of a material of thermal conductivity K2. The two ends of the combined system are maintained at two different temperatures. There is no loss of heat across the cylindrical surface and the system is in steady state. The effective thermal conductivity of the system is
View Solution
