Two nonconducting containers having volume V1 and V2 contain monoatomic and dimatomic gases respectivley. They are connected as shown in figure. Pressure and temperature in the two containers are P1,T1 and P2,T2 respectively. Initially stop cock is closed, if the stop coc is opened find the final pressure and temperature.
To solve the problem, we need to find the final pressure and temperature of the gases in two connected non-conducting containers after the stopcock is opened. The containers have volumes V1 and V2, and contain monoatomic and diatomic gases with initial pressures P1, P2 and temperatures T1, T2 respectively.
1. Calculate the Number of Moles:
- For the monoatomic gas in container 1:
n1=P1V1RT1
- For the diatomic gas in container 2:
n2=P2V2RT2
2. Total Number of Moles:
- The total number of moles after the stopcock is opened is:
n=n1+n2=P1V1RT1+P2V2RT2
3. Final Pressure and Temperature:
- After the stopcock is opened, the pressure and temperature will equalize. Let the final pressure be P and the final temperature be T.
- The total volume after opening the stopcock is V=V1+V2.
4. Using the Ideal Gas Law:
- The ideal gas law for the combined system gives:
P(V1+V2)=nRT
- Substituting for n:
P(V1+V2)=(P1V1RT1+P2V2RT2)RT
- Simplifying this gives:
P(V1+V2)=P1V1TT1+P2V2TT2
5. Energy Conservation:
- The conservation of energy can be expressed as:
32n1RT1+52n2RT2=32nRT+52nRT
- This leads to:
32(P1V1RT1)RT1+52(P2V2RT2)RT2=32nRT+52nRT
6. Final Temperature:
- Rearranging gives us the final temperature T:
T=32P1V1T2+52P2V2T132P1V1+52P2V2
7. Final Pressure:
- Finally, substituting T back into the equation for P:
P=3P1V1+5P2V23P1V1/T2+5P2V2/T1
Final Answers:
- Final Pressure:
P=3P1V1+5P2V23P1V1T2+5P2V2T1
- Final Temperature:
T=32P1V1T2+52P2V2T132P1V1+52P2V2
- For the monoatomic gas in container 1:
n1=P1V1RT1
- For the diatomic gas in container 2:
n2=P2V2RT2
- The total number of moles after the stopcock is opened is:
n=n1+n2=P1V1RT1+P2V2RT2
- After the stopcock is opened, the pressure and temperature will equalize. Let the final pressure be P and the final temperature be T.
- The total volume after opening the stopcock is V=V1+V2.
- The ideal gas law for the combined system gives:
P(V1+V2)=nRT
- Substituting for n:
P(V1+V2)=(P1V1RT1+P2V2RT2)RT
- Simplifying this gives:
P(V1+V2)=P1V1TT1+P2V2TT2
- The conservation of energy can be expressed as:
32n1RT1+52n2RT2=32nRT+52nRT
- This leads to:
32(P1V1RT1)RT1+52(P2V2RT2)RT2=32nRT+52nRT
- Rearranging gives us the final temperature T:
T=32P1V1T2+52P2V2T132P1V1+52P2V2
- Finally, substituting T back into the equation for P:
P=3P1V1+5P2V23P1V1/T2+5P2V2/T1
- Final Pressure:
P=3P1V1+5P2V23P1V1T2+5P2V2T1
- Final Temperature:
T=32P1V1T2+52P2V2T132P1V1+52P2V2
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Solved Examples14videos
KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Exercise 2.120videos
KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression2videos
KINETIC THEORY OF GASES
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Single correct anwer type14videos
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
Similar Questions
A nonconducting cylinder having volume 2V0 is partitioned by a fixed non conducting wall in two equal part. Partition is attached with a valve. Right side of the partition is a vacuum and left part is filled with a gas having pressure and temperature P0 and T0 respectively. If valve is opened find the final pressure and temperature of the two parts.
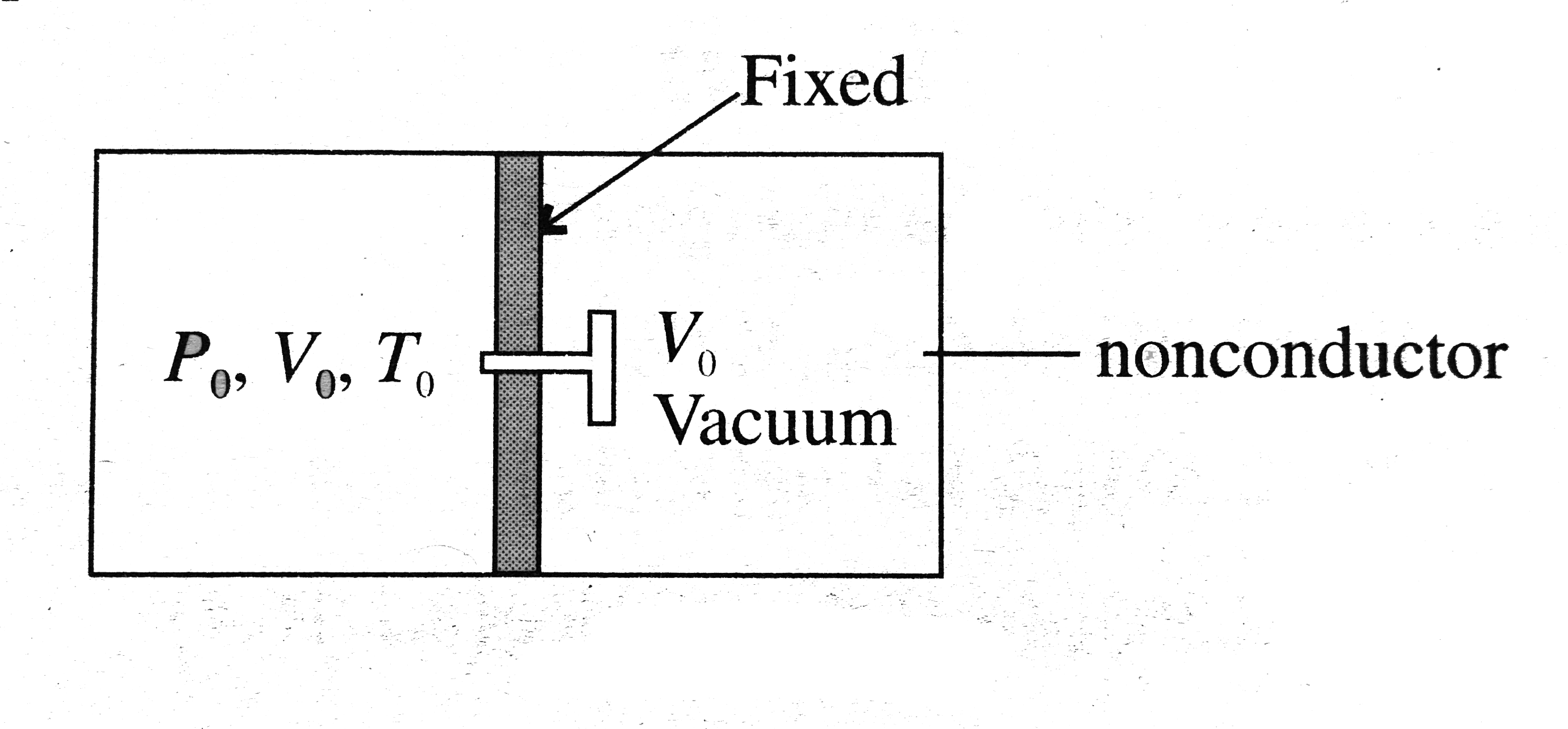 View Solution
View SolutionTwo adiabatic containers have volumes V1 and V2 respectively. The first container has monoatomic gas at pressure p1 and temperature T1. The second container has another monoatomic gas at pressure p2 and temperature T2. When the two containers are connected by a narrow tube, the final temperature and pressure of the gases in the containers are P and T respectively. Then
View SolutionThe ratio of pressure of the same gas in two containers is n1T1n2T2 where n1 & n2 are the number of moles and T1 & T2 are respective temperatures. If the containers are now joined find the ratio of final pressure to the temperature :
View SolutionThree containes of the same volume contain three different gases. The masses of the molecules are m1,m2 and m3 and the number of molecules in their respective containers are N1,N2 and N3. The gas pressure in the containers are P1,P2 and P3 respectively. All the gases are now mixed and put in one of the containers. The pressure P of mixture will be
View SolutionA monoatomic gas is enclosed in a nonconducting cylinder having a piston which can move freely. Suddenly gas is compressed to 1/8 of its initial volume. Find the final pressure and temperature if initial pressure and temperature are P0 and T0 respectively.
 View Solution
View SolutionTwo vessels of volume (V1)and(V2) contain the same ideal gas. The pressures in the vessels are (P1)and(P2) and the temperatures are (T1)and(T2) respectively . The two vessels are now connected to each other through a narrow tube. Assuming that no heat is exchanged between the surrounding and the vessels, find the common pressure and temperature attained after the connection.
View SolutionA monoatomic gas is enclosed in a non-conducting cylinder having a piston which can move freely. Suddenly gas is compressed to 1/8 of its initial volume. Find the final pressure and temperature if initial pressure and temperature are P0 and T0 respectively.
 View Solution
View SolutionA monoatomic gas at pressure P1 and volume V1 is compressed adiabatically to 18th of its original volume. What is the final pressure of gas.
View SolutionA cylindrical tube with adiabatic walls having volume 2V0contains an ideal monoatomic gas as shown in figure. The tube is divided into two equal parts by a fixed super conducting wall. Initially, the pressure and the temperature are P0,T0 on the left and 2P0,2T0 on the rigid. When system is left for sufficient amount of time the temperature on both sides becomes equal
 View Solution
View SolutionTwo containers of equal volume contain the same gas at pressure P1 and P2 and absolute temperature T1 and T2, respectively. On joining the vessels, the gas reaches a common pressure P and common temperature T. The ratio P/T is equal to
View Solution

