The ratio of pressure of the same gas in two containers is n1T1n2T2 where n1 & n2 are the number of moles and T1 & T2 are respective temperatures. If the containers are now joined find the ratio of final pressure to the temperature :
P1T2+P2T12T1T2
P1T1+P2T1T1T2
P1T1+P2T22T1T2
none of these
The correct Answer is:A
To solve the problem, we need to find the ratio of the final pressure to the temperature after the two containers of gas are joined. We will use the ideal gas law and the relationship between pressure, volume, temperature, and the number of moles.
1. Understanding the Initial Conditions:
- We have two containers with gases at different pressures, temperatures, and number of moles.
- The ratio of the pressures of the gases in the two containers is given by:
P1P2=n1T1n2T2
2. Using the Ideal Gas Law:
- The ideal gas law states that:
PV=nRT
- For both containers, we can express the pressures as:
P1=n1RT1VandP2=n2RT2V
3. Combining the Containers:
- When the two containers are joined, the total volume becomes 2V.
- The total number of moles of gas after mixing is n1+n2.
4. Applying the Ideal Gas Law to the Combined System:
- The pressure P in the combined volume can be expressed as:
P⋅(2V)=(n1+n2)RT
- Rearranging gives:
P=(n1+n2)RT2V
5. Finding the Ratio of Final Pressure to Temperature:
- We need to find the ratio PT:
PT=(n1+n2)R2V
6. Substituting for P1 and P2:
- From the earlier expressions for P1 and P2:
P1=n1RT1VandP2=n2RT2V
- We can express n1 and n2 in terms of P1 and P2:
n1=P1VRT1andn2=P2VRT2
7. Substituting Back into the Ratio:
- Substitute n1 and n2 into the ratio:
PT=(P1VRT1+P2VRT2)R2V
- Simplifying gives:
PT=12(P1T1+P2T2)
8. Final Result:
- Thus, the final ratio of pressure to temperature after the containers are joined is:
PT=12(P1T1+P2T2)
- We have two containers with gases at different pressures, temperatures, and number of moles.
- The ratio of the pressures of the gases in the two containers is given by:
P1P2=n1T1n2T2
- The ideal gas law states that:
PV=nRT
- For both containers, we can express the pressures as:
P1=n1RT1VandP2=n2RT2V
- When the two containers are joined, the total volume becomes 2V.
- The total number of moles of gas after mixing is n1+n2.
- The pressure P in the combined volume can be expressed as:
P⋅(2V)=(n1+n2)RT
- Rearranging gives:
P=(n1+n2)RT2V
- We need to find the ratio PT:
PT=(n1+n2)R2V
- From the earlier expressions for P1 and P2:
P1=n1RT1VandP2=n2RT2V
- We can express n1 and n2 in terms of P1 and P2:
n1=P1VRT1andn2=P2VRT2
- Substitute n1 and n2 into the ratio:
PT=(P1VRT1+P2VRT2)R2V
- Simplifying gives:
PT=12(P1T1+P2T2)
- Thus, the final ratio of pressure to temperature after the containers are joined is:
PT=12(P1T1+P2T2)
Topper's Solved these Questions
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Multiple Corrects
29 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Assertion-Reasoning
6 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Subjective
22 Videos
- KINETIC THEORY OF GASESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression
2 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Single correct anwer type
14 Videos
Similar Questions
Three perfect gases at absolute temperature T1,T2 and T3 are mixed. The masses f molecules are m1,m2 and m3 and the number of molecules are n1,n2 and n3 respectively. Assuming no loss of energy, the final temperature of the mixture is
View SolutionThree perfect gases at absolute temperature T1,T2 and T3 are mixed. The masses f molecules are m1,m2 and m3 and the number of molecules are n1,n2 and n3 respectively. Assuming no loss of energy, the final temperature of the mixture is
View SolutionTwo nonconducting containers having volume V1 and V2 contain monoatomic and dimatomic gases respectivley. They are connected as shown in figure. Pressure and temperature in the two containers are P1,T1 and P2,T2 respectively. Initially stop cock is closed, if the stop coc is opened find the final pressure and temperature.
View SolutionThree containes of the same volume contain three different gases. The masses of the molecules are m1,m2 and m3 and the number of molecules in their respective containers are N1,N2 and N3. The gas pressure in the containers are P1,P2 and P3 respectively. All the gases are now mixed and put in one of the containers. The pressure P of mixture will be
View SolutionTwo perfect gases (1) and (2) are at temperatures T1 and T2 . If the number of molecules of the two gases are n1 and n2 and the masses of the molecules m1 and m2, find the resulting temperature when the two gases are mixed. Assume that there is no loss of energy on mixing the two gases.
View SolutionTwo adiabatic containers have volumes V1 and V2 respectively. The first container has monoatomic gas at pressure p1 and temperature T1. The second container has another monoatomic gas at pressure p2 and temperature T2. When the two containers are connected by a narrow tube, the final temperature and pressure of the gases in the containers are P and T respectively. Then
View SolutionTwo perfect gases at absolute temperature T1andT2 are mixed. There is no loss of energy. The masses of the molecules are m1andm2. The number of molecules in the gases are n1andn2. The temperature of the mixture is
View SolutionThe absolute value of the sum of first 20 terms of series, if Sn=n+12 and Tn−1Tn=1n2−1, where n is odd, given Sn and Tn denotes sum of first n terms and nth terms of the series
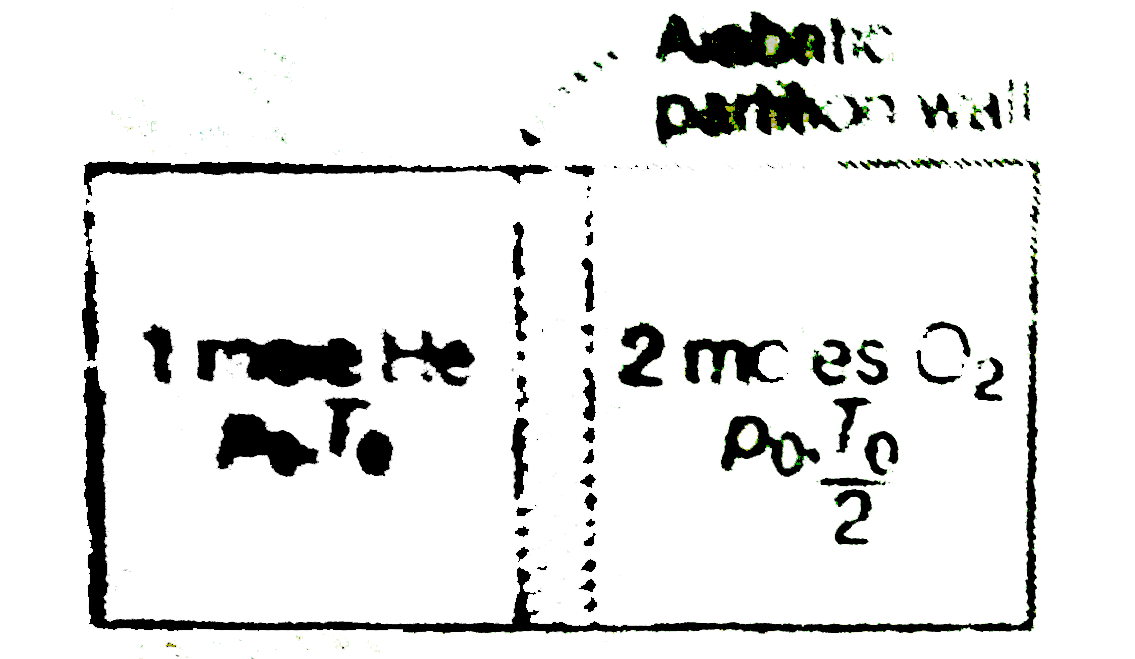
View SolutionConsider the adjacent figure. A piston divides a cylindrical container into two equal parts. The lets part contains 1 mole of helium gas and the right part contains two moles or oxygen gas. The initial temperatures and pressures of the gases in the left chamber are T0 and p0 and the right chamber are T02 and p0 respectively as shown in the figure. The piston as well as the walls of the container are adiabatic. After removal of the piston, gases mix homoganeously and the final pressure becomes p=4n13p0. Find the value of n.
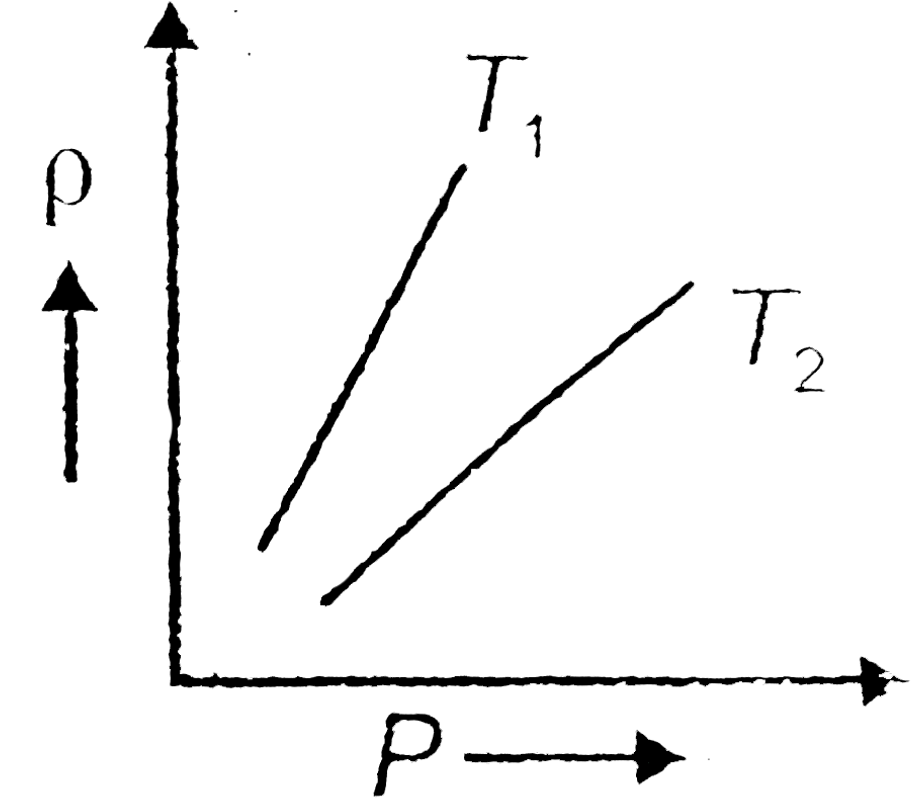
View SolutionThe density (ρ) versus pressure (P) graphs of a given mass of an ideal gas is shown at two temperatures T1andT2. Then relation between T1andT2 may be
View Solution
