Fig shows the variation in the internal energy U with the volume V of 2.0 mol of an ideal gas in a cyclic process abcda. The temperatures of the gas at b and c are 500 K and 300 K respectively. Calculate the heat absorbed by the gas during the process.
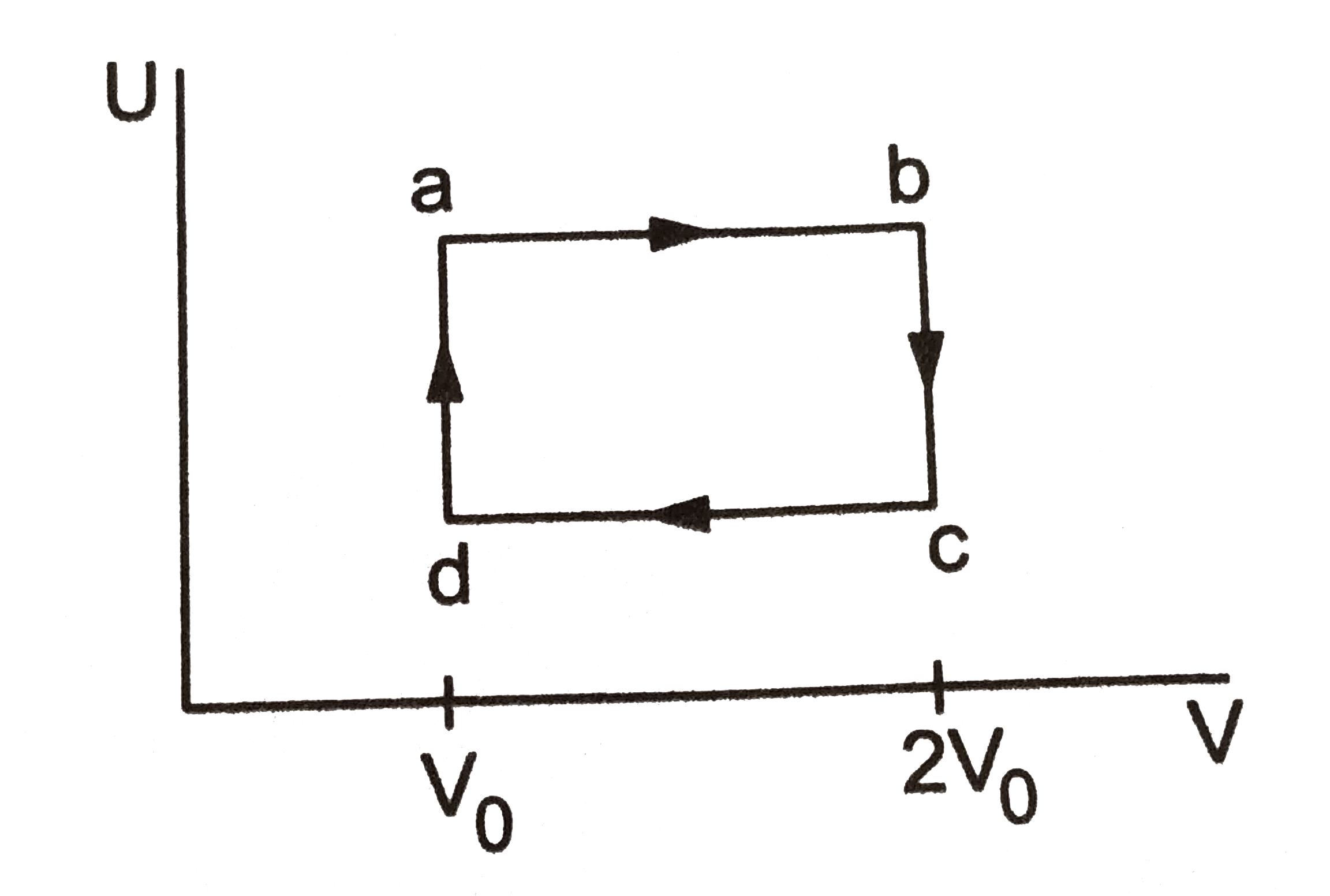
Change in internal energy for cyclic process (ΔU)=0
For process a→b, (P - constant)
Wa→b=PΔV=nRΔT=−400R
For process b→c (T - constant)
Wb→c=−2R(300)1n2)
For process c→d (P - constant)
Wc→d=+400R
For process d→a (T - constant)
Wd→a=+2R(500)1n2
Net work,
(ΔW)=Wa→b+Wb→c+Wc→d+Wd→a
ΔW=400R1n2
dQ=dU+dW, first law of thermodynamics
dQ=400R1n2
Topper's Solved these Questions
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Single Correct
140 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Multiple Corrects
29 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Exercise 2.2
28 Videos
- KINETIC THEORY OF GASESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression
2 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Single correct anwer type
14 Videos
Similar Questions
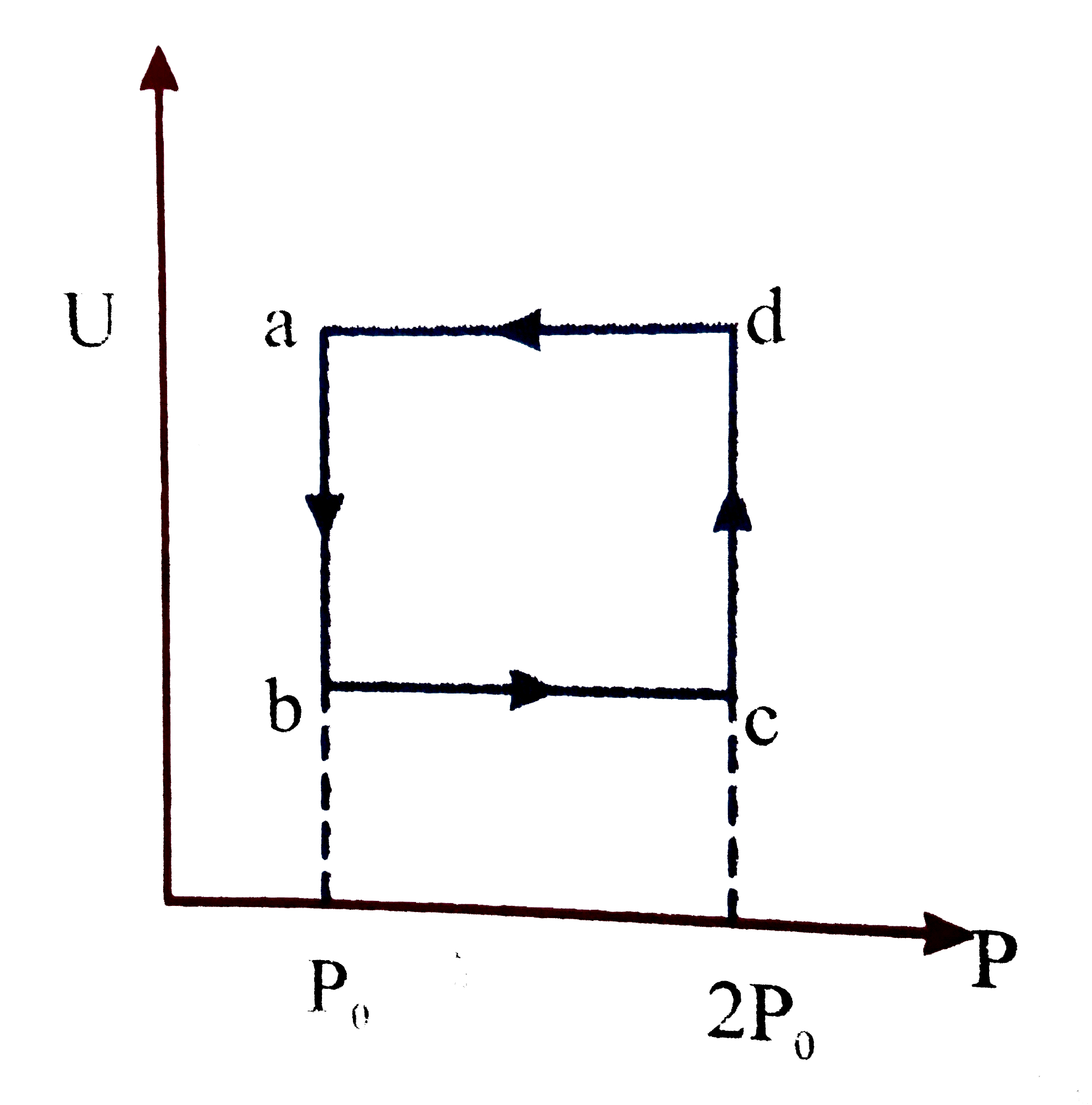
Figure shows the variation of internal energy (U) with the pressure (P) of 2.0 mole gas in cyclic process abcda.The temperature of gas at c and d are 300and500K respectively. The heat absorbed by the gas during the process is X×10Rln2 . Find the value of x.
View Solutionconsider the cyclic process ABCA on a sample of 2.0 mol of an ideal gas as shown in the fig. temperature of the gas at A and B are 300 K and 500 k respectively. A total of 1200 J heat is withdrawn from the sample in the process. Find the work done by the gas in part BC. take R=8.3JK−1mol−1

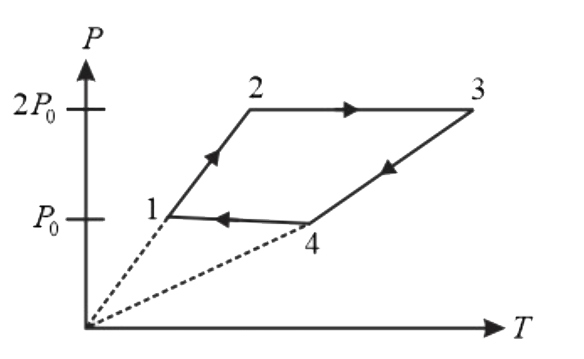
View SolutionOne mole of an ideal monoatomic gas undergoes a cyclic process, as shown in the figure. If the temperature of the gas at state 1 is 300 K and at state 4 is 500 K, then heat exchanged during process 2→3, is
View SolutionOne mole of an ideal gas is taken through a cyclic process. The minimum temperature during the cycle is 300K. Then, net exchange of heat for complete cycle is
View SolutionIn figure, a cyclic process ABCA of 3 moles of an ideal gas is given. The temperature of the gas at B and C are 500k and 1000K respectively. If work done on the gas in process CA is 2500J then find the net heat absorbed or released by an idela gas. Take R=25/3J/mol−K.
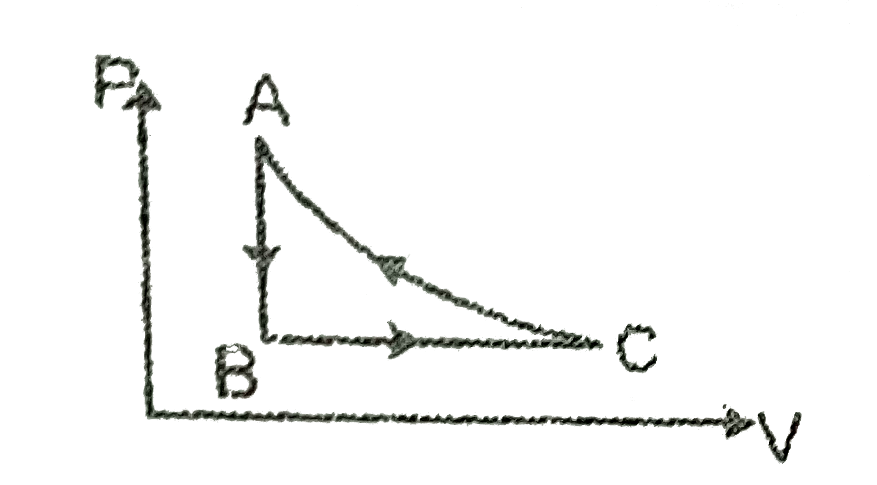
View SolutionFigure, shows the variation of potential energy (U) of 2 mol of Argon gas with its density in a cyclic process ABCA. The gas was initiallly in the state A whose pressure and temperature are PA=2atm,TA=300K, respectively. It is also stated the path AB is a rectangular hyperbola and the internal energy of the gas at state C is 3000r. Based on the above information answer the following question :
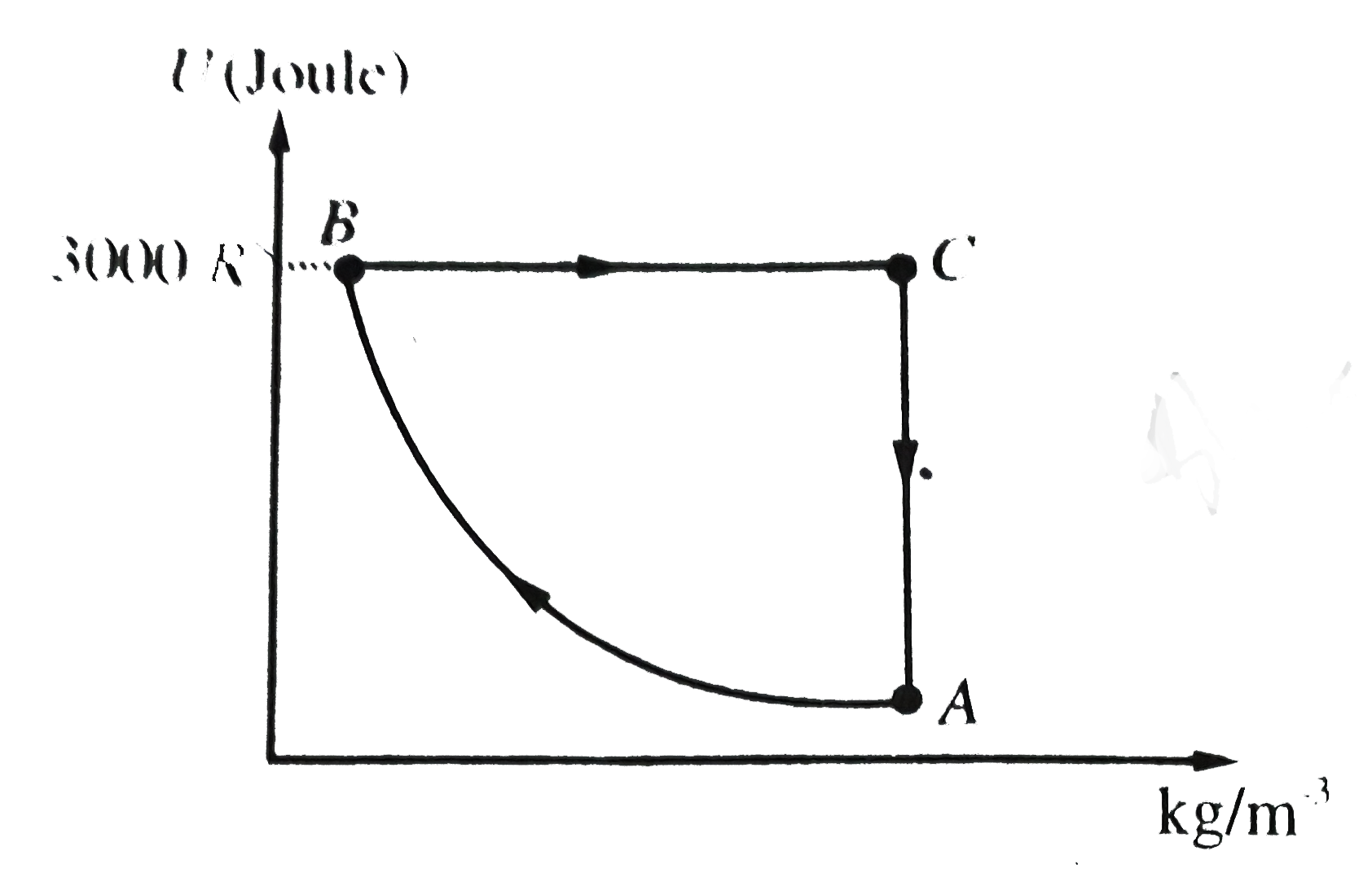
The heat supplied to the gas in the process AB is
View SolutionFigure, shows the variation of potential energy (U) of 2 mol of Argon gas with its density in a cyclic process ABCA. The gas was initiallly in the state A whose pressure and temperature are PA=2atm,TA=300K, respectively. It is also stated the path AB is a rectangular hyperbola and the internal energy of the gas at state C is 3000r. Based on the above information answer the following question :
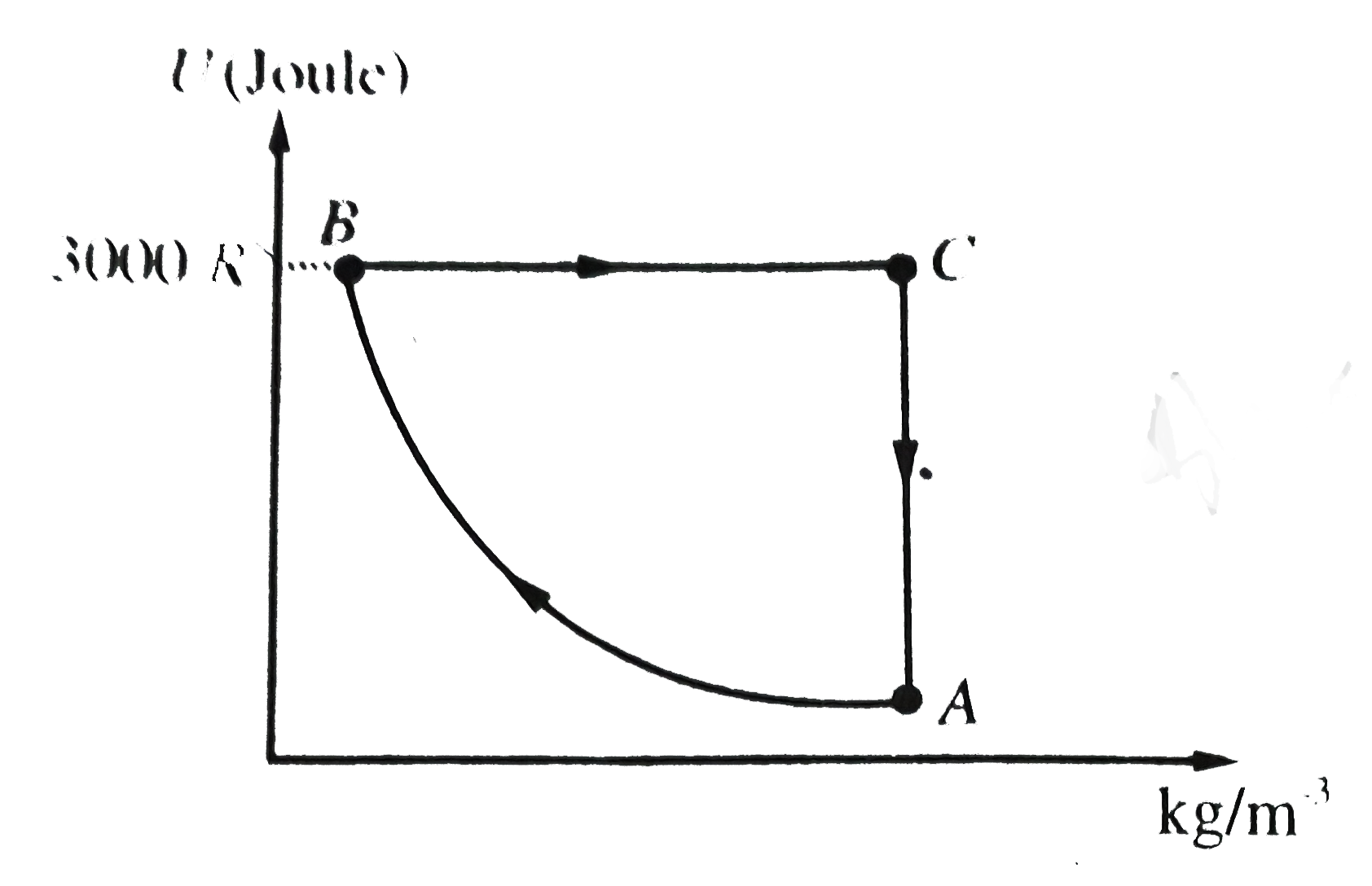
Heat supplied in the process CA is
View SolutionA sample of ideal gas is taken through the cyclic process shown in the figure. The temerauture of the gas in state A is TA =200 K. In states B and C the temperature of the gas is the same.
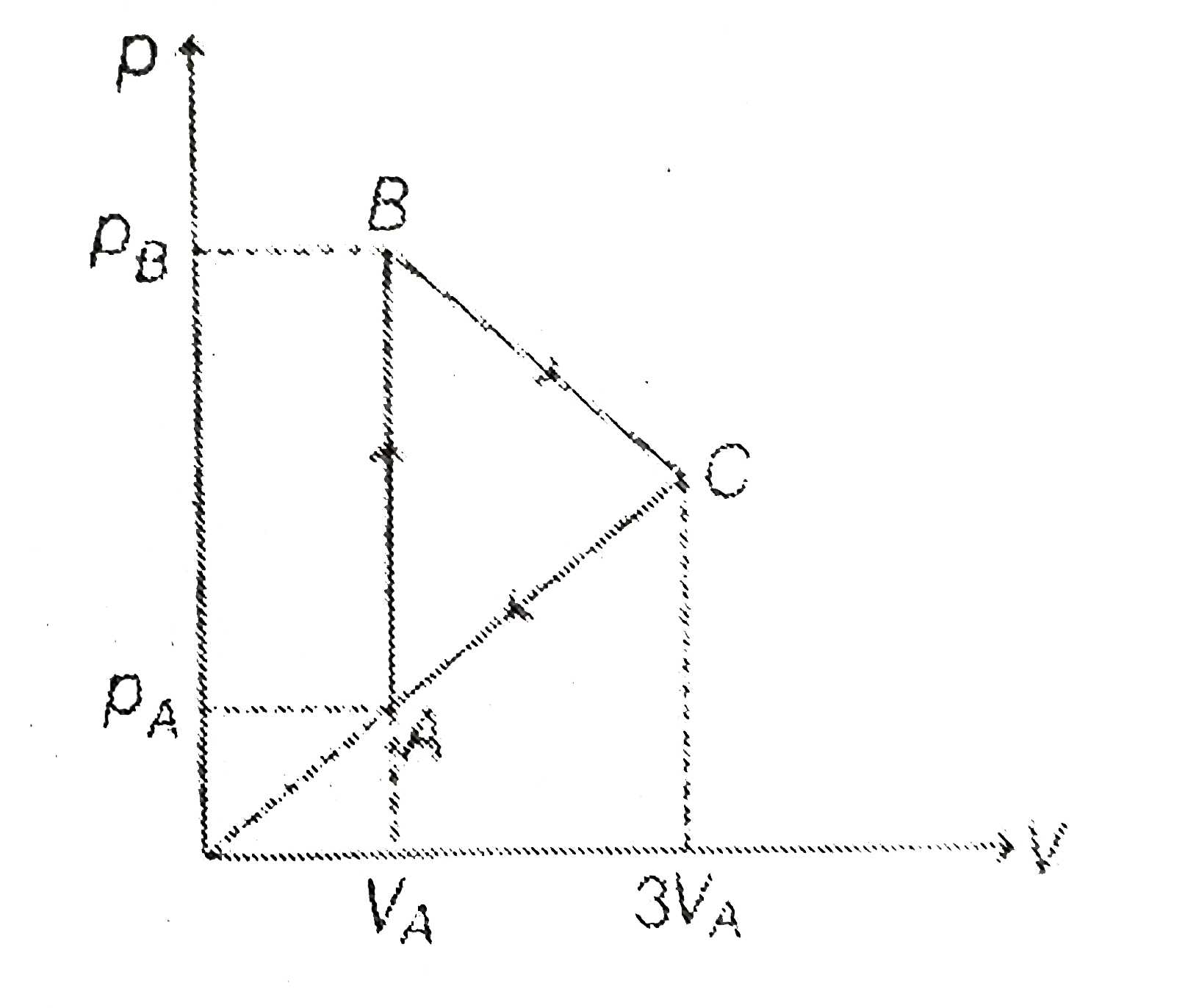
Net work done by the gas in the process is
View SolutionFigure shows the variation of the internal energy U with the density ρ of an ideal monoatomic gas for a therodynamic process AB. Process AB is a part of arectangular hyperbola. Find the work done (in joule) by gas in process AB.
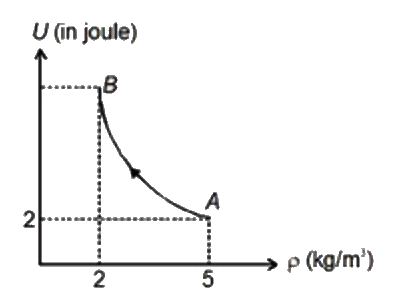
View SolutionOne mole of a diatomic ideal gas undergoes a cyclic process ABC as shown in figure. The process BC is adiabatic. The temperature at A,B and C are 400K, 800K and 600K respectively. Choose the correct statement:
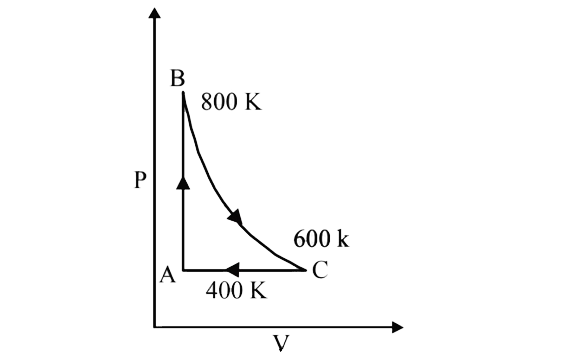
View Solution
