An ideal gas is initially at temperature T and volume V. ITS volume is increased by ΔV due to an increase in temperature ΔT, pressure remaining constant. The quantity δ=ΔV/VΔT varies with temperature as
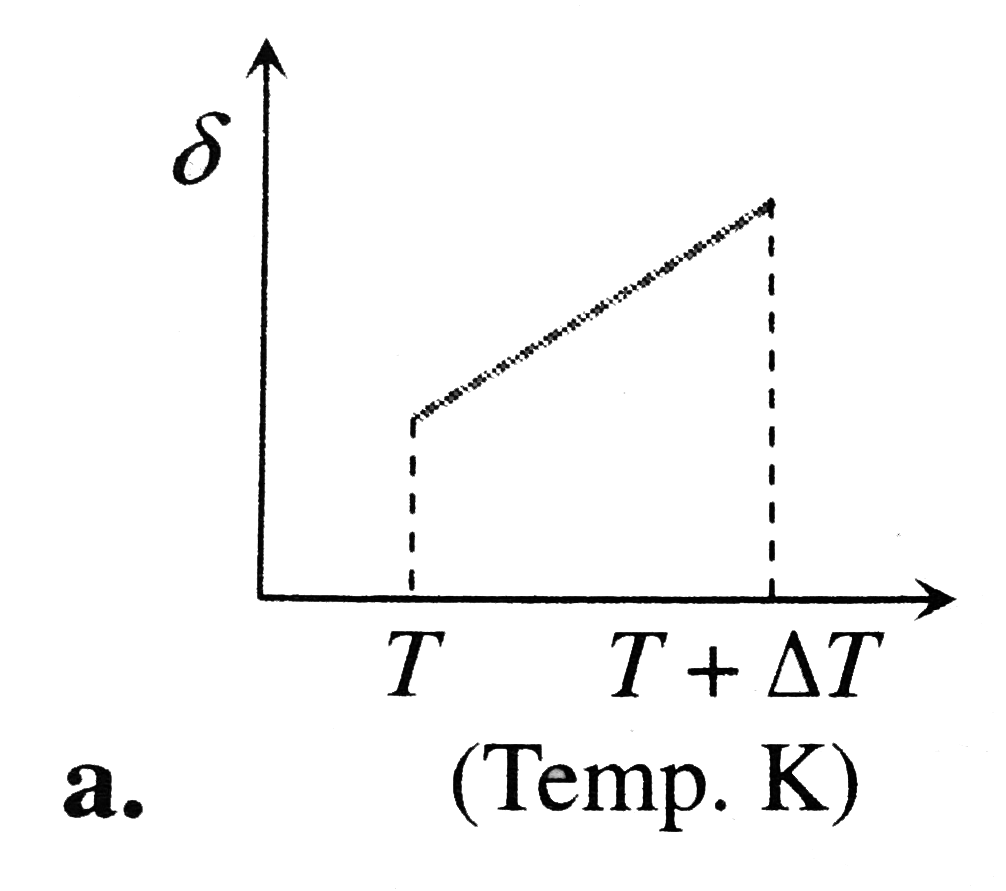
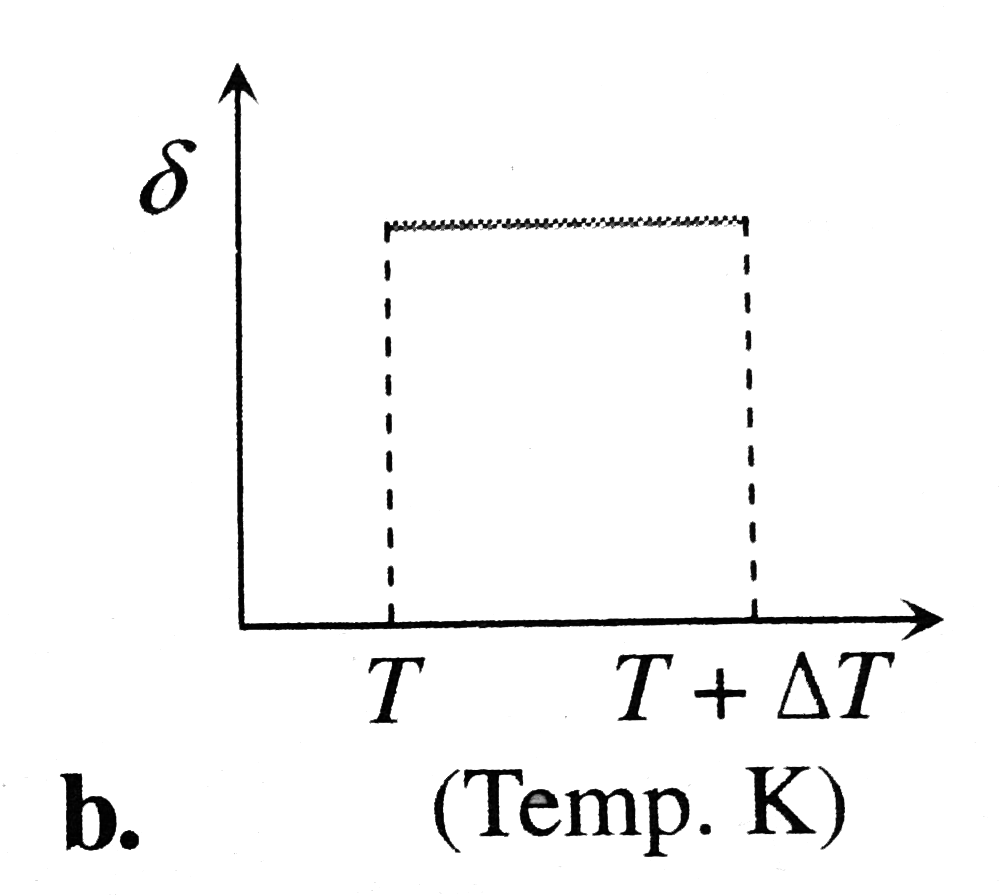


The correct Answer is:C
c. From ideal gas equation
PV=RT
PΔT=RΔT
Dividing Eq. (ii) by Eq. (i), we get
ΔTV=ΔTT⇒ΔVVΔT=1T=δ (given)
∴Δ=1T
So the graph between δ and T will be a rectangular hyperbola.
Topper's Solved these Questions
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Multiple Corrects
29 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Assertion-Reasoning
6 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Subjective
22 Videos
- KINETIC THEORY OF GASESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression
2 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Single correct anwer type
14 Videos
Similar Questions
Knowledge Check
If the pressure and the volume of certain quantity of ideal gas are halved, then its temperature
Ais doubledBbecomes one-fourthCremains constantDbecome four timesAs the temperature increases, average kinetic energy of molecules increases. What would be the effect of increase of temperature on pressure provided the volume is constant ?
AIncreasesBDecreasesCRemains sameDBecomes half
By increasing temperature of a gas by 6∘C its pressure increases by 0.4%, at constant volume. Then initial temperature of gas is
View SolutionThe pressure p and volume V of an ideal gas both increase in a process.
View SolutionAt constant temperature if the pressure of an ideal gas is increased by 10% then its volume must decrease by
View SolutionAt constant temperature if the pressure of an ideal gas is increased by 10% then its volume must decrease by
View SolutionAs the temperature increases, average kinetic energy of molecules increases. What would be the effect of increase of temperature on pressure provided the volume is constant ?
View SolutionWhen volume of system is increased two times and temperature is decreased half of its initial temperature, then pressure becomes ………….
View Solution
