The pressure p and volume V of an ideal gas both increase in a process.
such a process is not possible.
The work done by the system is positive.
The tempreture of the system must increase.
Heat supplied to the gas is equal to the change in internal energy.
The correct Answer is:B, C
To analyze the process where both the pressure P and volume V of an ideal gas increase, we can follow these steps:
1. Understanding Work Done by the Gas:
- The work done W by the gas during expansion is given by the formula:
W=PΔV
- Here, ΔV=Vf−Vi (final volume - initial volume). Since the volume is increasing, ΔV is positive.
Conclusion: The work done by the system is positive.
2. Analyzing the Ideal Gas Law:
- The ideal gas law is expressed as:
PV=nRT
- Given that both P and V are increasing, we can infer that the temperature T must also increase to satisfy the equation, assuming the number of moles n and the gas constant R remain constant.
Conclusion: The temperature of the system must increase.
3. Applying the First Law of Thermodynamics:
- The first law of thermodynamics states:
ΔQ=ΔW+ΔU
- Where ΔQ is the heat added to the system, ΔW is the work done by the system, and ΔU is the change in internal energy.
- Since we have established that the work done ΔW is positive (not zero), it implies that heat supplied to the gas cannot be equal to the change in internal energy ΔU unless the work done is zero.
Conclusion: The heat supplied to the gas is not equal to the change in internal energy.
4. Final Evaluation of Options:
- Based on our analysis:
- Option 1: Incorrect (such a process is possible).
- Option 2: Correct (the work done by the system is positive).
- Option 3: Correct (the temperature of the system must increase).
- Option 4: Incorrect (heat supply to the gas is not equal to the change in internal energy).
Final Answer:
The correct options are Option 2 and Option 3.
- The work done W by the gas during expansion is given by the formula:
W=PΔV
- Here, ΔV=Vf−Vi (final volume - initial volume). Since the volume is increasing, ΔV is positive.
- The ideal gas law is expressed as:
PV=nRT
- Given that both P and V are increasing, we can infer that the temperature T must also increase to satisfy the equation, assuming the number of moles n and the gas constant R remain constant.
- The first law of thermodynamics states:
ΔQ=ΔW+ΔU
- Where ΔQ is the heat added to the system, ΔW is the work done by the system, and ΔU is the change in internal energy.
- Since we have established that the work done ΔW is positive (not zero), it implies that heat supplied to the gas cannot be equal to the change in internal energy ΔU unless the work done is zero.
- Based on our analysis:
- Option 1: Incorrect (such a process is possible).
- Option 2: Correct (the work done by the system is positive).
- Option 3: Correct (the temperature of the system must increase).
- Option 4: Incorrect (heat supply to the gas is not equal to the change in internal energy).
The correct options are Option 2 and Option 3.
Topper's Solved these Questions
Similar Questions
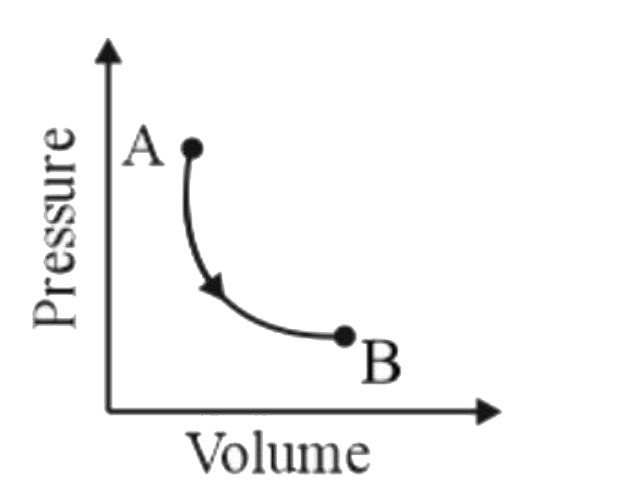
The pressure P and volume V of an ideal gas both decreases in a process.
View SolutionThe pressure and volume of an ideal gas are related as pα1v2 for process A→B as shown in figure . The pressure and volume at A are 3p0andv0 respectively and pressure B is p0 the work done in the process A→B is found to be [x−√3]p0v0 find
View SolutionThe variation of pressure P with volume V for an ideal diatomic gas is parabolic as shown in the figure . The molar species heat of the gas during this process is
View SolutionIf both the temperature and the volume of an ideal gas are doubled, the pressure
View SolutionThe pressure v/s volume graph of an ideal gas is given different thermodynamics process which of the following option relevant in order : (Isochoric, isobaric, isothermal, adiabatic)
_2019_CBT2_E01_013_Q01.png)
View SolutionThe given (p - U) graph shows the variation of internal energy of an ideal gas with increase in pressure. Which of the following pressure - volume graph is equivalent to this graph ?
 .
.
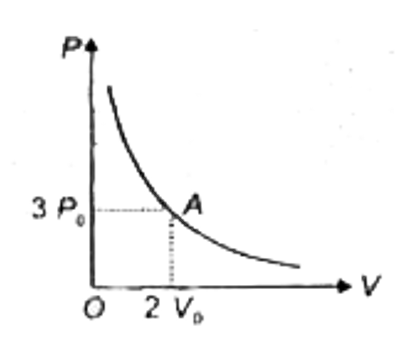
View SolutionThe variation of pressure P with volume V for an ideal monatomic gas during an adiabatic process is shown in figure . At point A the magnitude of rate of change of pressure with volume is
View SolutionThe figures given below show different processes (relating pressure P and volume V) for a given amount of an ideal gas. W is work done by the gas and ΔQ is heat absorbed by the gas.
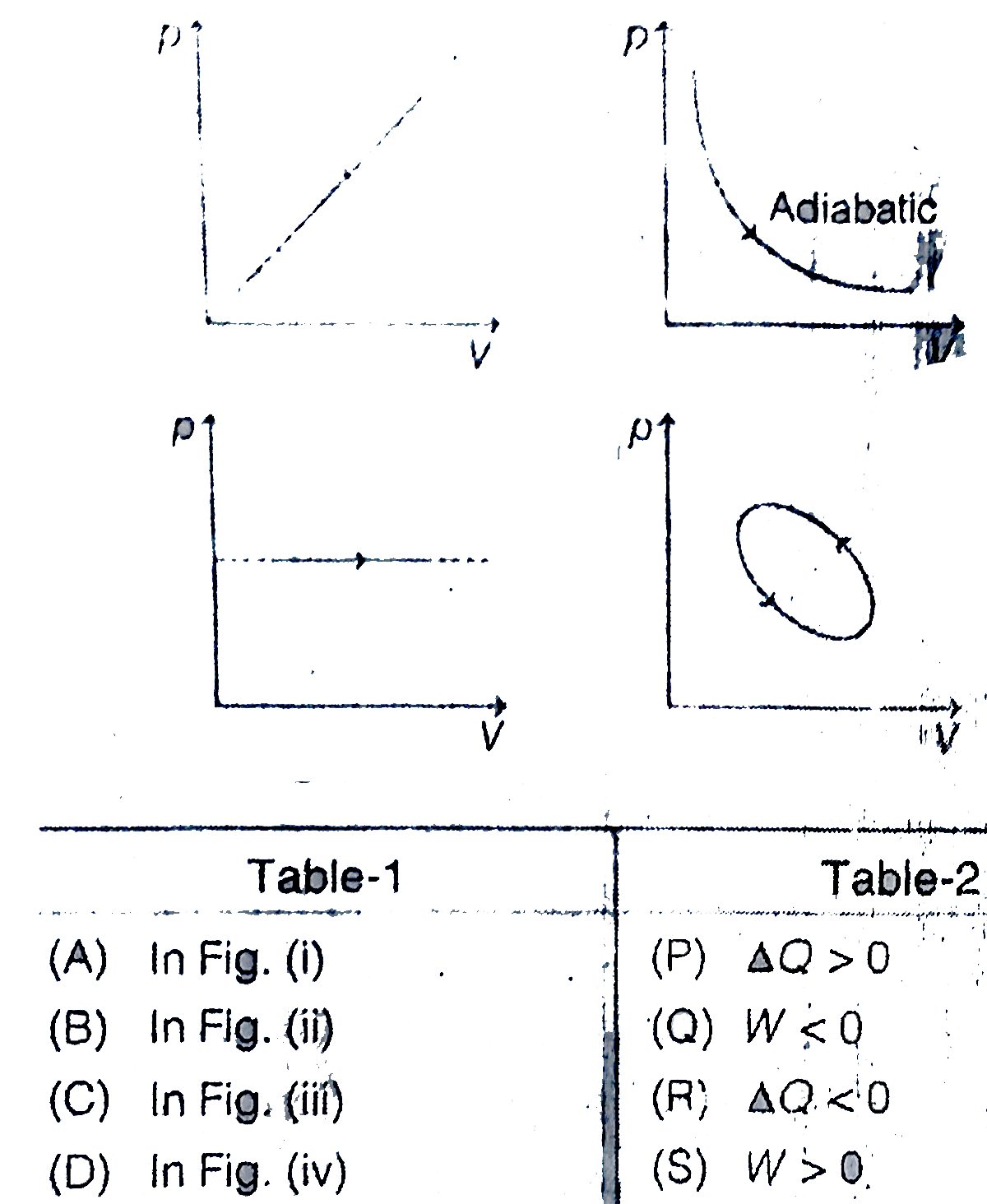
View SolutionA sample of an ideal gas with initial pressure 'P' and volume 'V' is taken through an isothermal process during which entropy change is found to be DS. The work done by the gas is
View SolutionA monoatomic gas undergoes a process in which the pressure (P) and the volume (V) of the gas are related as PV−3=constant. What will be the molar heat capacity of gas for this process?
View Solution
