A spring block pendulum is shown in figure . The system is hanging in equilibrium. A bullet of mass m/2 moving at a speed u bites the block from downwards direction and gets embedded in it. Find the amplitude of oscillation of the block now.

If block is in equilibrium , then spring must be at some steretch if it is h, have mg=kh.
If a bullet of mass m/2 gets embedded in the block, due to this inelastic impact its new mass becoms 3m/2 and new mean positionof the block will be , say at a depth h1 from old mean position, then we must have
32mg=k(h+h1)
3m2g=k(h+h1)
h1=mg2k(asmg=kh)
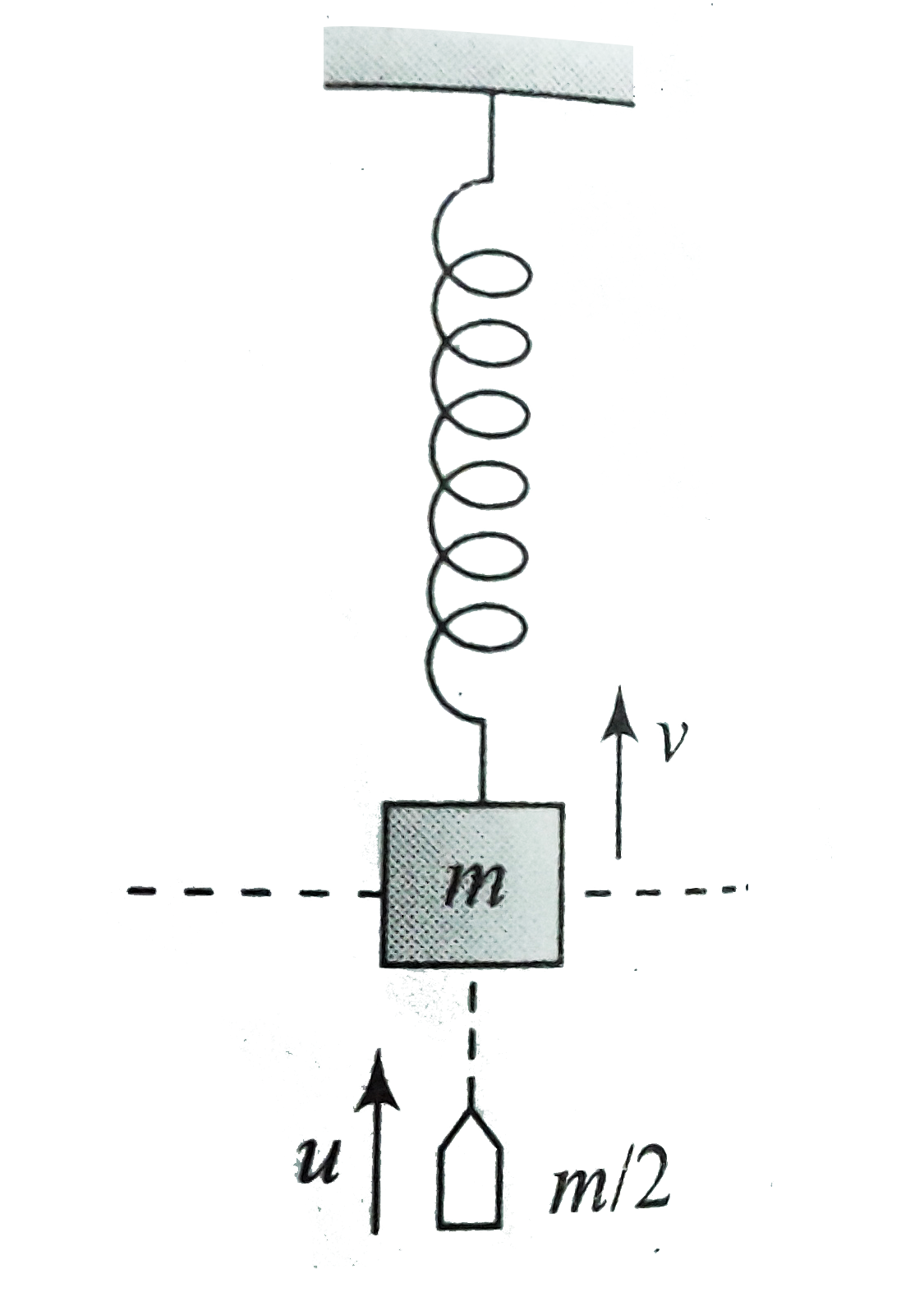
just after impact due to inelastic collition if the velocity of block becomes v, we have, according to momentum conservation.
m2μ=3m2νorν=u3
Now the block executes SHM and at t=0 block is at a distance h=mg2k above its mean position and having a velocity u/3. If amplitude of oscillation is A, we have
u3=ω√A2−(mg2k)2
or u29=2k3m[A2−(mg2k)2]
[as for this spring block system omega =√k(3m/2)]
A=√μ26k+(mg2k)2
Now time taken by partical to reach the topmost point can be obtained by circular motion representation as shown in figure. This figure shows the position of block P and its corresponding circular motion partical p0 at thet=0, Block P will reach its upper extereme position when partical P0 will traveres the angle θ and reach the topmost point as P0 moves at constant angular velocity ω, it will take a time given as
t=θω=cos−1(h1/A)√k3m/2=√3m2kcos−1(3mg2kA)

Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Exercise 4.1
23 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Exercise 4.2
23 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Single correct anwer type
14 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
Similar Questions
A bullet of mass m moving with velocity v strikes a block of mass M at rest and gets embedded into it. The kinetic energy of the composite block will be
View SolutionA bullet of mass m strikes a block of mass M. The bullet remains embedded in the block. Find the amplitude of the resulting SHM.

View SolutionFigure shown a spring block system hanging in equilibrium. If a velocity v0 is imparted to the block in downwards direction . Find the amplitude of SHM of the block and the time after which it will reach a point at half the amplitude of block

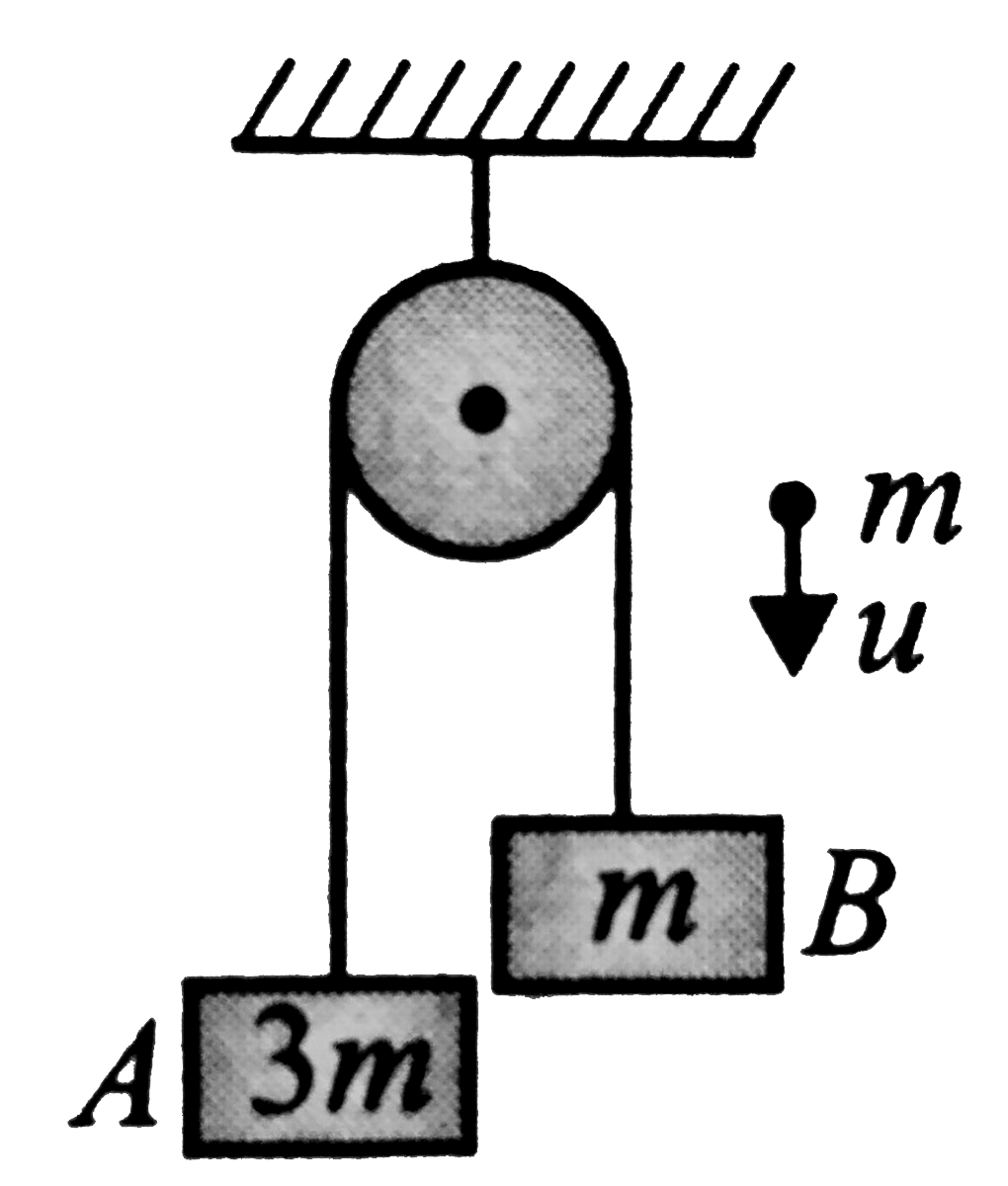
View SolutionA system of two blocks A and B are connected by an inextensible massless string as shown in Fig. The pulley is massless and frictionless. Initially, the system is at rest. A bullet of mass m moving with a velocity u as shown hits block If and gets embedded into it. The impulse imparted by tension force to the block of mass 3m is
View SolutionBlock of mass m2 is in equilibrium and at rest. The mass m1 moving with velocity u vertically downwards collids with m2 and sticks to it. Find the energy of oscillation.
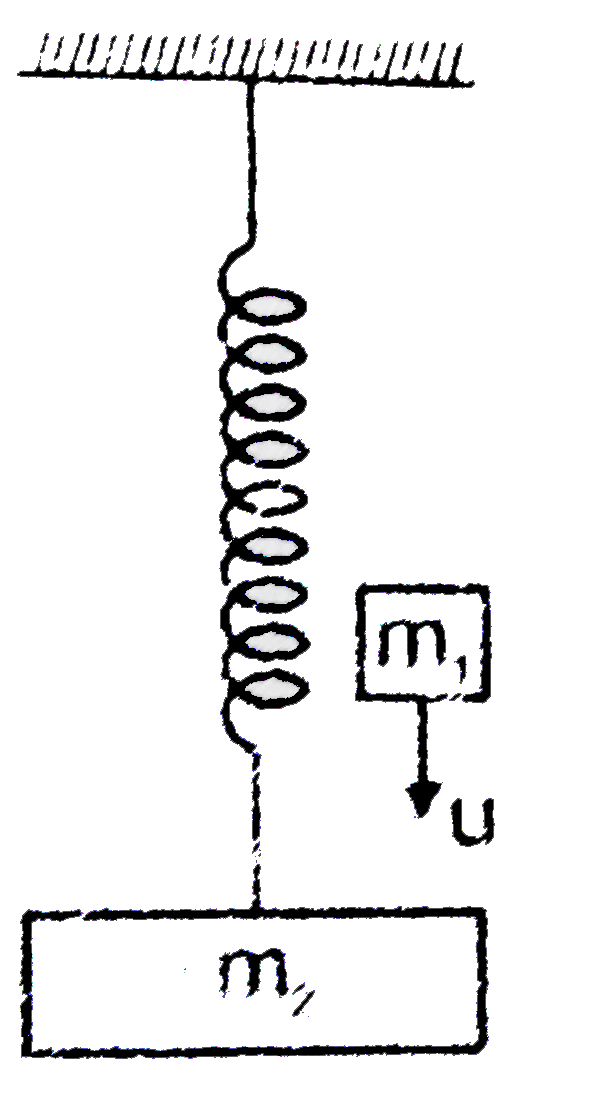
View SolutionBlock of mass m2 is in equilibrium and at rest. The mass m1 moving with velocity u vertically downwards collids with m2 and sticks to it. Find the energy of oscillation.

View SolutionTwo blocks of masses m and 3m are connected by an inextensible string and the string passes over a fixed pulley which is massless and frictionless. A bullet of mass m moving with a velocity 'u' hits the hanging block of mass 'm' and gets exbedded in it. Find the height through which block A rises after the collision.
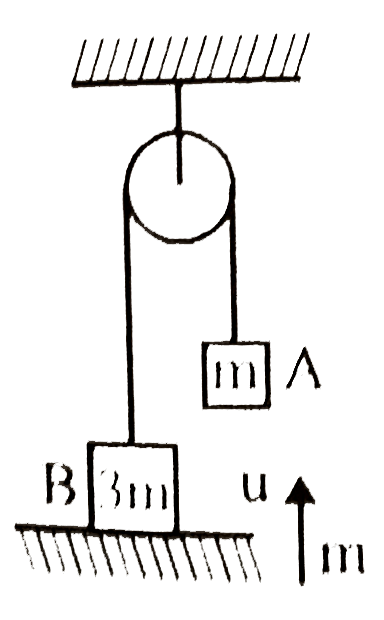
View Solution
System is shown in the figure and man is pulling the rope from both sides with constant speed u find the speed of the block.
View Solution
System is shown in the figure and man is pulling the rope from both sides with constant speed u find the speed of the block.
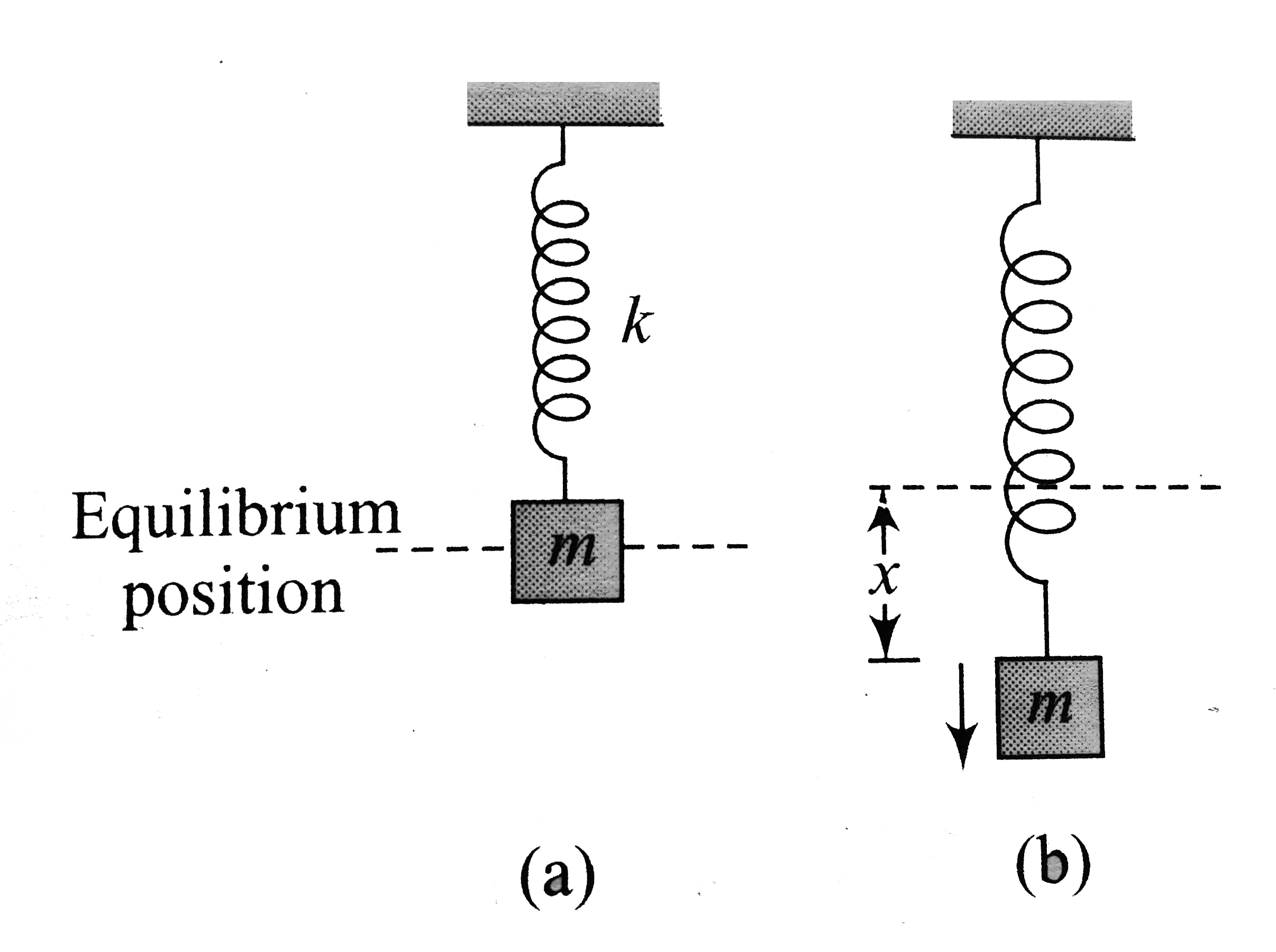
View SolutionFigure shown a spring block system hanging in equilibrium. The block of system is pulled down by the distance x and imparted a velocity v in downward direction as shown in figure. Find the time it will take to reach its mean position. Also find the maximum distance to which if will move before returning back towards mean position.
View Solution