Two particles move parallel to x - axis about the origin with the same amplitude and frequency. At a certain instant they are found at distance A3 from the origin on opposite sides but their velocities are found to be in the same direction. What is the phase difference between the two ?
cos−1(79)
cos−1(59)
cos−1(49)
cos−1(19)
The correct Answer is:A
To solve the problem, we need to find the phase difference between two particles moving parallel to the x-axis with the same amplitude and frequency. Let's break down the solution step by step.
Step 1: Understand the Situation
We have two particles moving along the x-axis with the same amplitude A and frequency ω. At a certain instant, they are at positions +A3 and −A3 respectively. Their velocities are in the same direction.
Step 2: Write the Position Equations
For simple harmonic motion, the position of the particles can be described by:
- Particle 1: x1=Asin(ωt)
- Particle 2: x2=Asin(ωt+ϕ)
Where ϕ is the phase difference we need to find.
Step 3: Set Up the Equations
From the problem, we know:
- For Particle 1: x1=A3
- For Particle 2: x2=−A3
Substituting these into the equations:
1. A3=Asin(ωt)
2. −A3=Asin(ωt+ϕ)
Step 4: Simplify the Equations
From the first equation:
sin(ωt)=13
From the second equation:
sin(ωt+ϕ)=−13
Step 5: Use the Sine Addition Formula
Using the sine addition formula:
sin(ωt+ϕ)=sin(ωt)cos(ϕ)+cos(ωt)sin(ϕ)
Substituting the known values:
−13=(13)cos(ϕ)+cos(ωt)sin(ϕ)
Step 6: Find cos(ωt)
To find cos(ωt), we can use the identity sin2(θ)+cos2(θ)=1:
cos(ωt)=√1−sin2(ωt)=√1−(13)2=√1−19=√89=2√23
Step 7: Substitute Back
Now substitute cos(ωt) back into the equation:
−13=(13)cos(ϕ)+(2√23)sin(ϕ)
Step 8: Rearranging the Equation
Multiply through by 3 to eliminate the denominators:
−1=cos(ϕ)+2√2sin(ϕ)
Step 9: Solve for ϕ
Rearranging gives:
cos(ϕ)+2√2sin(ϕ)+1=0
This is a linear equation in terms of sin(ϕ) and cos(ϕ). We can solve this equation to find ϕ.
Step 10: Determine Possible Values of ϕ
After solving the equation, we find that the possible values for ϕ are:
- ϕ=cos−1(79) or ϕ=180∘
However, since both particles are moving in the same direction, ϕ=180∘ is not a valid solution.
Final Answer
Thus, the phase difference between the two particles is:
ϕ=cos−1(79)
---
We have two particles moving along the x-axis with the same amplitude A and frequency ω. At a certain instant, they are at positions +A3 and −A3 respectively. Their velocities are in the same direction.
For simple harmonic motion, the position of the particles can be described by:
- Particle 1: x1=Asin(ωt)
- Particle 2: x2=Asin(ωt+ϕ)
From the problem, we know:
- For Particle 1: x1=A3
- For Particle 2: x2=−A3
1. A3=Asin(ωt)
2. −A3=Asin(ωt+ϕ)
From the first equation:
sin(ωt)=13
sin(ωt+ϕ)=−13
Using the sine addition formula:
sin(ωt+ϕ)=sin(ωt)cos(ϕ)+cos(ωt)sin(ϕ)
−13=(13)cos(ϕ)+cos(ωt)sin(ϕ)
To find cos(ωt), we can use the identity sin2(θ)+cos2(θ)=1:
cos(ωt)=√1−sin2(ωt)=√1−(13)2=√1−19=√89=2√23
Now substitute cos(ωt) back into the equation:
−13=(13)cos(ϕ)+(2√23)sin(ϕ)
Multiply through by 3 to eliminate the denominators:
−1=cos(ϕ)+2√2sin(ϕ)
Rearranging gives:
cos(ϕ)+2√2sin(ϕ)+1=0
After solving the equation, we find that the possible values for ϕ are:
- ϕ=cos−1(79) or ϕ=180∘
Thus, the phase difference between the two particles is:
ϕ=cos−1(79)
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Multiple Correct35videos
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Assertion Reasoning6videos
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Subjective21videos
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger11videos
KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type3videos
MISCELLANEOUS KINEMATICS
Similar Questions
Two particles move parallel to x−axis about the origin with same amplitude 'a' and frequency ω. At a certain instant they are found at a distance a/3 from the origin on opposite sides but their velocities are in the same direction. What is the phase difference between the two?
View SolutionTwo particles execute SHM of same amplitude and frequency on parallel lines. They pass one another when moving in opposite directions each time their displacement is half of their amplitude. What is the phase difference between them?
View Solution
Knowledge Check
- Question 1 - Select One
Two particles execute SHM of same amplitude and frequency on parallel lines. They pass one another when moving in opposite directions each time their displacement is one third their amplitude. What is the phase difference between them?
A0B2π3CπDπ6 - Question 2 - Select One
Two particles execute SHMs of the same amplitude and frequency along the same straight line. They cross one another when going in opposite direction. What is the phase difference between them when their displacements are half of their amplitudes ?
A60∘B30∘C120∘D150∘
Two bodies performing S.H.M. have same amplitude and frequency. Their phases at a certain instant are as shown in the figure. The phase difference between them is
_E01_002_Q01.png) View Solution
View SolutionA particle is moving parallel to x-axis as shown in the figure. The angular velocity of the particle about the origin is
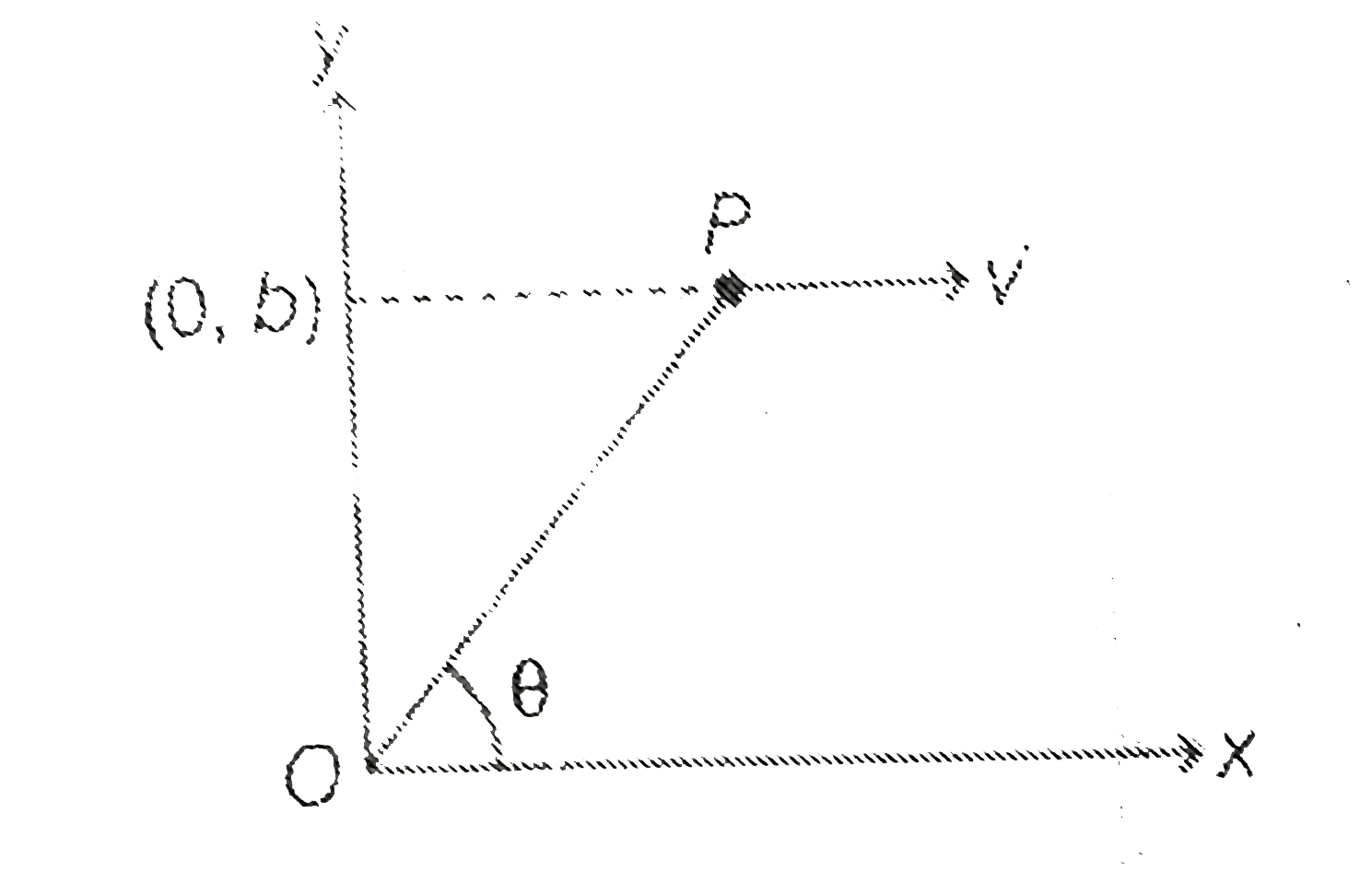 View Solution
View SolutionTwo particles execute simple harmonic motion of the same amplitude and frequency along close parallel lines. They pass each other moving in opposite directions each time their displacement is half their amplitude. Their phase difference is
View SolutionTwo particles undergo SHM along parallel lines with the same time period (T) and equal amplitudes. At particular instant, one particle is at its extreme position while the other is at its mean position. The move in the same direction. They will cross each other after a further time.
View SolutionTwo particles are executing simple harmonic of the same amplitude (A) and frequency ω along the x-axis . Their mean position is separated by distance Xo. (Xo>A). If the maximum separation between them is (Xo+A), the phase difference between their motion is:
View SolutionTwo particles are in SHM with the same amplitude and frequency along the same line and about the same point. If the maximum separation between them is √3 times their amplitude, the phase difference between them is 2πn. Find value of n
View Solution

