In the figure shown, mass 2m connected with a spring of force constant k is at rest and in equilibrium. A particle of mass m is released from height 4.5mg/k from 2m . The particle stick to the block. Neglecting the duration of collision find time from the release of m to the moment when the spring has maximum compression.
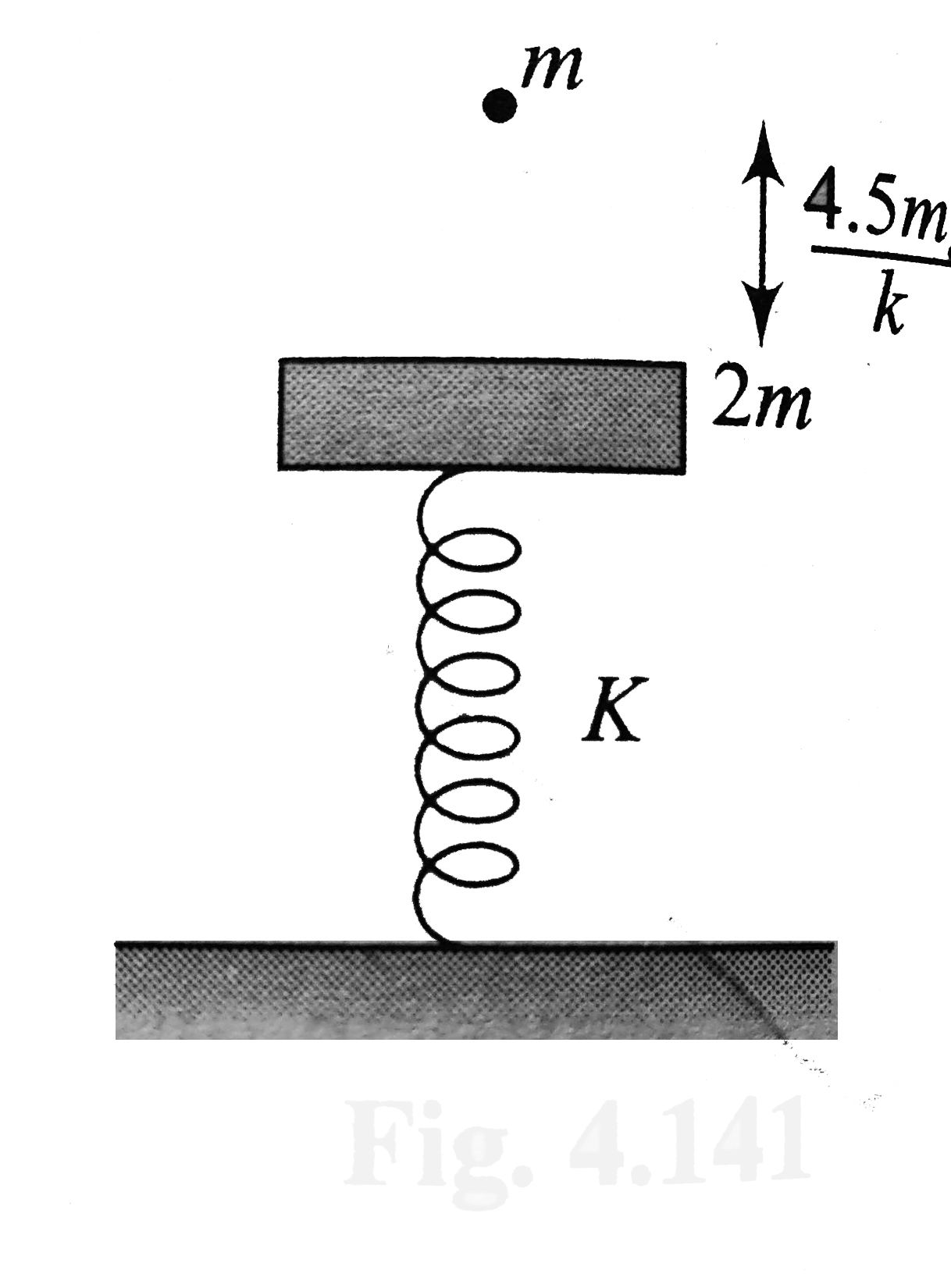
Velocity of the particle just before collision.
u=√2g×4.5mgK⇒u=3g√mK
Now it collides with the plate.
Now just after collision velocity (V) of the system of plate + particle'
mu=3mV⇒V=u3=g√mK
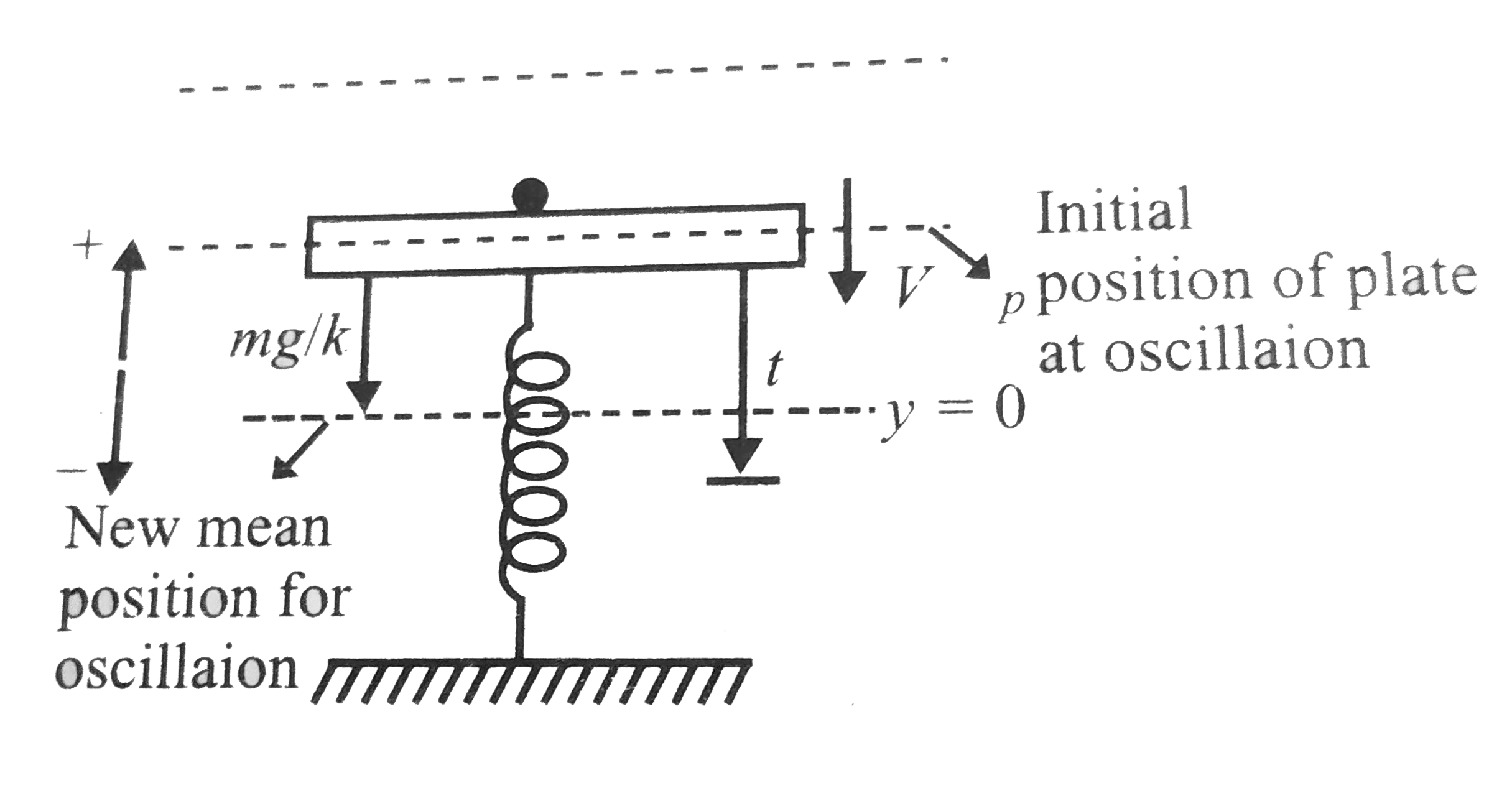
Now the system performs SHM with time period
T=2π√3mKω=√K3m and mean position as mgK
distance below the point of collision.
Let the equation of motion is
y=Asin(ωt+ϕ) .(i)
v=dydt=Aωcos(ωt+ϕ) ..(ii)
At t=0,y=mgK and v=g√mK
From eqs (i) and (ii) mgK=Asinϕ ..(iii)
A=2mgK ..(iv)
From Eqs. (iii) and (iv), ϕ=5πK y=2mgKsin(√K3mt+5π6)
Hence equation of SHM should be
y=−A=−2mgK=2mgKsin(√K2mt+5π6)
The plate will be at rest again when
y=−A=−2mgK=2mgKsin(√K3m+5π6)
⇒sin(√K3mt+5π6)=−1=sin(3π)2
⇒√K3mt+5π6=3π2⇒=2π3√3mK
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Subjective type
2 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Single correct Answer Type
29 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Comprehension
33 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
Similar Questions
In the figure shown, mass 2m connected with a spring of force constant k is at rest and in equilibrium. A partical of mass m is released from height 4.5mg/k from 2m . The partical stick to the block. Neglecting the duration of collision find time from the release of m to the moment when the spring has maximum compression.

View SolutionIn the figure shown mass 2m is at rest and in equilibrium. A particle of mass m is released from height 4.5mgk from plate. The particle sticks to the plate. Neglecting the duration of collision. Starting from the when the particles sticks to plate to the time when the spring is in maximum compression for the first time is 2π√mak then find a.
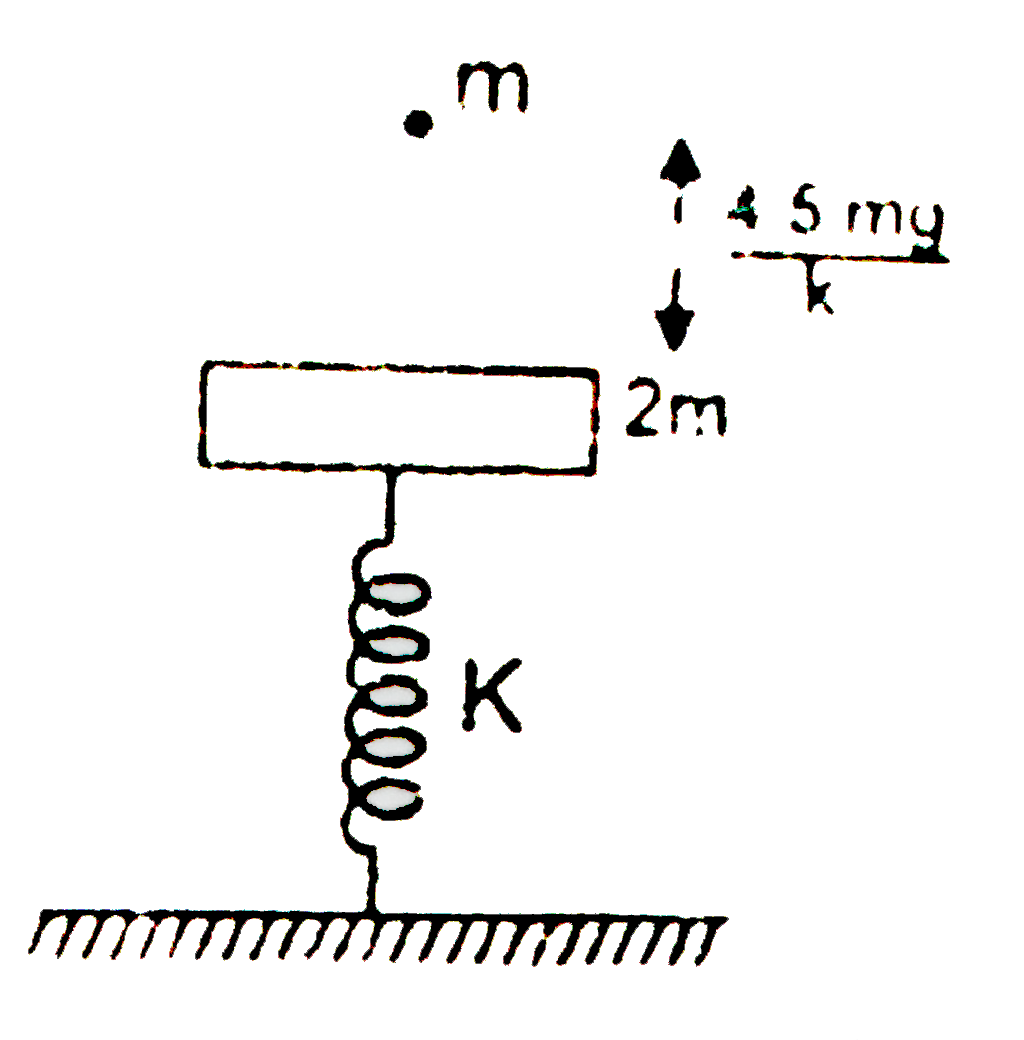
View SolutionA block of mass m is released from a height h from the top of a smooth surface. There is an ideal spring of spring constant k at the bottom of the track. Find the maximum compression in the spring (Wedge is fixed)

View SolutionA 2 kg block is connected with two springs of force constants k1=100N/m and k2=300N/m as shown in figure. The block is released from rest with the springs unstretched. The acceleration of the block in its lowest postion is (g=10m/s2)

View SolutionA block of mass m suspended from a spring of spring constant k. Find the amplitude of S.H.M.
View SolutionA particle of mass 'm' is attached to three identical springs A,B and C each of force constant 'K' as shown in figure. If the particle of mass 'm' is pushed slightly against the spring 'A' and released the period of oscillations is

View SolutionA particle of mass 'm' is attached to three identical springs A,B and C each of force constant 'K' as shown in figure. If the particle of mass 'm' is pushed slightly against the spring 'A' and released the period of oscillations is

View SolutionA body of mass m is released from a height h to a scale pan hung from a spring. The spring constant of the spring is k, the mass of the scale pan is negligible and the body does not bounce relative to the pan, then the amplitude of vibration is
View SolutionA body of mass m is released from a height h to a scale pan hung from a spring. The spring constant of the spring is k, the mass of the scale pan is negligible and the body does not bounce relative to the pan, then the amplitude of vibration is
View SolutionIn an ideal pulley particle system, mass m2 is connected with a vertical spring of stiffness k. If mass m2 is released from rest, when the spring is underformed, find the maximum compression of the spring.

View Solution
