A particle of mass m is attached to one end of a mass-less spring of force constant k, lying on a frictionless horizontal plane. The other end of the spring is fixed. The particle starts moving horizontally from its equilibrium position at time with an initial velocity . when the speed of the particle is , it collides elastically with a rigid wall. After this collision
the speed of the particle when it returns to its equilibrium position is .
the time at which the particle passes through the equilibrium position for the first time is
the time at which the maximum compression of the spring occurs is
the time at which the particle passes through the equilibrium position for the second time is .
The correct Answer is:A, D
To solve the problem step by step, we need to analyze the motion of the particle attached to the spring and its interaction with the wall.
Step 1: Understand the motion of the particle
The particle starts from the equilibrium position with an initial velocity u0. The motion of the particle can be described by simple harmonic motion (SHM) since it is attached to a spring.
Step 2: Write the equation of motion
The position x of the particle at time t can be expressed as:
x(t)=Asin(ωt)
where A is the amplitude of the motion and ω is the angular frequency given by:
ω=2πT
where T is the time period of the motion, given by:
T=2π√mk
Step 3: Determine the velocity of the particle
The velocity v of the particle can be derived from the position function:
v(t)=dxdt=Aωcos(ωt)
At the moment of collision with the wall, the speed of the particle is given as 0.5u0. Therefore, we set:
Aωcos(ωt)=0.5u0
Step 4: Relate the maximum velocity to the initial conditions
The maximum velocity vmax occurs when the particle is at the equilibrium position (where x=0):
vmax=Aω=u0
From this, we can express A in terms of u0:
A=u0ω
Step 5: Substitute and solve for cos(ωt)
Substituting A into the velocity equation:
u0ω⋅ωcos(ωt)=0.5u0
This simplifies to:
cos(ωt)=0.5
Thus, we find:
ωt=π3(or 60∘)
Step 6: Calculate the time t
Using ω=2πT:
2πTt=π3
This gives:
t=T6
Step 7: Determine the total time to return to equilibrium
The time taken to return to the equilibrium position after the collision is also T6. Therefore, the total time to return to the equilibrium position after the collision is:
ttotal=T6+T6=T3
Step 8: Substitute T into the equation
Substituting T=2π√mk:
ttotal=2π√mk3
Conclusion
The total time taken for the particle to return to its equilibrium position after colliding with the wall is:
ttotal=2π3√mk
The particle starts from the equilibrium position with an initial velocity u0. The motion of the particle can be described by simple harmonic motion (SHM) since it is attached to a spring.
The position x of the particle at time t can be expressed as:
x(t)=Asin(ωt)
where A is the amplitude of the motion and ω is the angular frequency given by:
ω=2πT
where T is the time period of the motion, given by:
T=2π√mk
The velocity v of the particle can be derived from the position function:
v(t)=dxdt=Aωcos(ωt)
At the moment of collision with the wall, the speed of the particle is given as 0.5u0. Therefore, we set:
Aωcos(ωt)=0.5u0
The maximum velocity vmax occurs when the particle is at the equilibrium position (where x=0):
vmax=Aω=u0
From this, we can express A in terms of u0:
A=u0ω
Substituting A into the velocity equation:
u0ω⋅ωcos(ωt)=0.5u0
This simplifies to:
cos(ωt)=0.5
Thus, we find:
ωt=π3(or 60∘)
Using ω=2πT:
2πTt=π3
This gives:
t=T6
The time taken to return to the equilibrium position after the collision is also T6. Therefore, the total time to return to the equilibrium position after the collision is:
ttotal=T6+T6=T3
Substituting T=2π√mk:
ttotal=2π√mk3
The total time taken for the particle to return to its equilibrium position after colliding with the wall is:
ttotal=2π3√mk
Topper's Solved these Questions
- ARCHIVES 2 VOLUME 6Book:CENGAGE PHYSICS ENGLISHChapter:ARCHIVES 2 VOLUME 6Exercise:Comprehension
Explore 12 Videos
- ARCHIVES 2 VOLUME 6Book:CENGAGE PHYSICS ENGLISHChapter:ARCHIVES 2 VOLUME 6Exercise:Integer
Explore 4 Videos
- ARCHIVES 2 VOLUME 6Book:CENGAGE PHYSICS ENGLISHChapter:ARCHIVES 2 VOLUME 6Exercise:Single Correct
Explore 51 Videos
- ARCHIVES 1 VOLUME 6Book:CENGAGE PHYSICS ENGLISHChapter:ARCHIVES 1 VOLUME 6Exercise:Integer
Explore 4 Videos
- BASIC MATHEMATICSBook:CENGAGE PHYSICS ENGLISHChapter:BASIC MATHEMATICSExercise:Exercise 2.6
Explore 20 Videos
Similar Questions
A particle of mass 3 kg , attached to a spring with force constant 48Nm−1execute simple harmonic motion on a frictionless horizontal surface. The time period of oscillation of the particle, is seconds , is
View SolutionA particle of mass m is fixed to one end of a massless spring of spring constant k and natural length l0. The system is rotated about the other end of the spring with an angular velocity ω ub gravity-free space. The final length of spring is
View Solution
Knowledge Check
A 10 kg mass is connected at one end of a massless spring with force constant k = 1000 N/m, keeping other end fixed in a horizontal plane as shown in the fig. 15.6
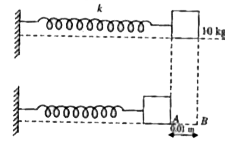 If the sytem is displaced by 0.01 m from its equilibrium position A to a point B, then the acceleration of the system is A10ms−2B1ms−2C−1ms−2D−10ms−2
If the sytem is displaced by 0.01 m from its equilibrium position A to a point B, then the acceleration of the system is A10ms−2B1ms−2C−1ms−2D−10ms−2
A particle of mass m is attached to one end of a light inextensible string and the other end of the string is fixed in vertical plane as shown. Particle is given a horizontal velocity u=√52gl

The maximum angle made by the string with downward vertical is
View SolutionA mass of 0.2 kg is attached to the lower end of a massless spring of force constant 200Nm the other end of which is fixed to a rigid support. Study the following statements.
View SolutionA block of mass m is kept on a rough horizontal surface and is attached with a massless spring of force constant k. The minimum constant force applied on the other end of the spring of lift the block is
View SolutionA particles of mass m is fixed to one end of a light spring of force constant k and unstreatched length l. the system is rotated about the other end of the spring with an angular velocity ω in gravity free space. The increase in length of the spring is

View SolutionA mass of 0.2 hg is attached to the lower end of a massles spring of force constant 200Nm the opper end of which is fixed to a rigid support. Study the following statements.
View SolutionA block of mass m, attached to a spring of spring constant k, oscilltes on a smooth horizontal table. The other end of the spring is fixed to a wall. If it has speed v when the spring is at its naturla lenth, how far will it move on the table before coming to an instantaneous rest?
View SolutionA block of mass m is attached to one end of a mass less spring of spring constant k. the other end of spring is fixed to a wall the block can move on a horizontal rough surface. The coefficient of friction between the block and the surface is μ then the compession of the spring for which maximum extension of the spring becomes half of maximum compression is .
View Solution