An object is moving with a uniform acceleration which is parallel to its instantaneous direction of motion. The dispalcement (s)-velocity (v) graph of this object is.


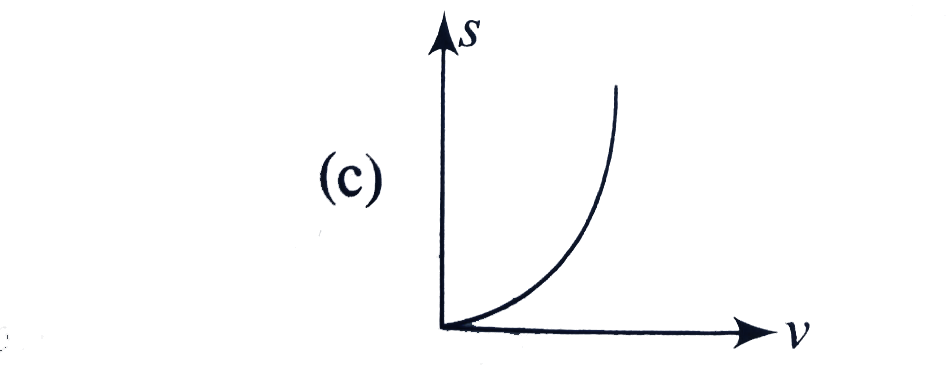

The correct Answer is:C
To solve the problem of finding the displacement (s) - velocity (v) graph for an object moving with uniform acceleration in the direction of its motion, we can follow these steps:
1. Understand the Motion:
The object is moving with uniform acceleration (A) in the direction of its initial velocity (u). We need to analyze the relationship between displacement (s) and velocity (v).
2. Use the Kinematic Equation:
We can use the kinematic equation that relates initial velocity, final velocity, acceleration, and displacement:
v2=u2+2as
Here, u is the initial velocity, v is the final velocity, a is the uniform acceleration, and s is the displacement.
3. Assume Initial Conditions:
For simplicity, let’s assume the initial velocity u=0. This means the equation simplifies to:
v2=2as
4. Rearranging the Equation:
Rearranging the equation gives us:
s=v22a
This shows that displacement s is proportional to the square of the velocity v.
5. Identify the Graph Type:
The equation s=12av2 is in the form of a quadratic equation, which represents a parabola. Specifically, it indicates that as v increases, s increases quadratically.
6. Graph Characteristics:
Since s is plotted on the y-axis and v on the x-axis, the graph will be an upward-facing parabola starting from the origin (0,0).
7. Conclusion:
Thus, the displacement-velocity graph for the object moving with uniform acceleration is an upward-facing parabola.
Final Answer:
The displacement (s) - velocity (v) graph of the object is an upward-facing parabola.
The object is moving with uniform acceleration (A) in the direction of its initial velocity (u). We need to analyze the relationship between displacement (s) and velocity (v).
We can use the kinematic equation that relates initial velocity, final velocity, acceleration, and displacement:
v2=u2+2as
Here, u is the initial velocity, v is the final velocity, a is the uniform acceleration, and s is the displacement.
For simplicity, let’s assume the initial velocity u=0. This means the equation simplifies to:
v2=2as
Rearranging the equation gives us:
s=v22a
This shows that displacement s is proportional to the square of the velocity v.
The equation s=12av2 is in the form of a quadratic equation, which represents a parabola. Specifically, it indicates that as v increases, s increases quadratically.
Since s is plotted on the y-axis and v on the x-axis, the graph will be an upward-facing parabola starting from the origin (0,0).
Thus, the displacement-velocity graph for the object moving with uniform acceleration is an upward-facing parabola.
The displacement (s) - velocity (v) graph of the object is an upward-facing parabola.
Similar Questions
An object is moving with a uniform acceleration which is parallel to its instantaneous direction of motion. The displacement velocity (v) graph of this object is
View SolutionThe displacement (s)- velocity ( v ) graph of a particle if it starts moving from rest with a uniform acceleration which is parallel to its instantaneous direction of motion is
View SolutionWhich of the quantity, velocity or acceleration determines the direction of motion ?
View SolutionThe slope of velocity-time graph for uniform motion of an object is
View SolutionAssertion: A uniform circular motion is an acceleration motion.
Reason: Direction of acceleration is parallel to velocity vector.
View SolutionState which of the following situations are possible and give an example for each of these :
(a) An body with a constant acceleration but with zero velocity.
(b) An object moving with an acceleration but with uniform speed
(c) An object moving in a certain direction with an acceleration in the perpendicular direction.
View SolutionIf the object is moving with uniform velocity in a given interval of time, then the average speed and instantaneous velocity are equal, why?
View SolutionSay Yes or No:
a. Can an object moving towards north have acceleration towards south?
b. Can an object reverse the direction of its motion even thouth it has reverse the direcleration?
C. Can an object reverse the derction of its acceleration even though it continues to move in the same dirction?
d. Average speed is the magnitude of average velocity
e. At any instant of time. the directions of change in velocity and acceleration are differnt.
View SolutionAn object A is moving with 5 m/s and B is moving with 20 m/s in the same direction. (Positive x-axis). Find a) velocity of B relative to A.
b) Velocity of A relative to B
View SolutionAn object A is moving with 5 m/s and B is moving with 20 m/s in the direction . (positive x-axis )
find velocity of A with respect to B .
View Solution
