The displacement (s)- velocity ( v ) graph of a particle if it starts moving from rest with a uniform acceleration which is parallel to its instantaneous direction of motion is
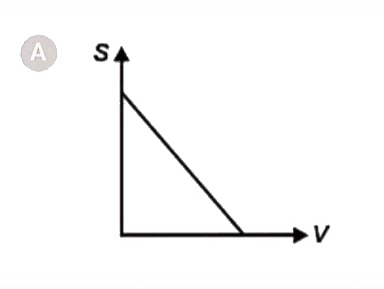
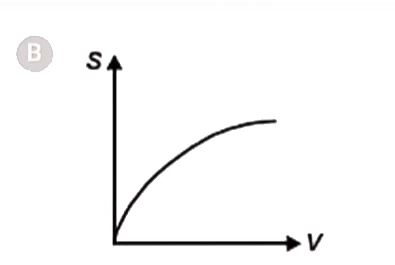
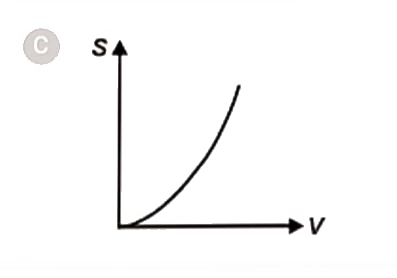

The correct Answer is:C
To solve the problem of determining the displacement (s) - velocity (v) graph of a particle that starts moving from rest with uniform acceleration parallel to its instantaneous direction of motion, we can follow these steps:
1. Understanding Initial Conditions:
- The particle starts from rest, which means at time t=0, the initial velocity v0=0 and the initial displacement s0=0.
2. Using the Equation of Motion:
- Since the particle is moving with uniform acceleration a, the equations of motion can be applied. The velocity v at any time t can be expressed as:
v=u+at
where u=0 (initial velocity). Thus, we have:
v=at
3. Relating Displacement and Velocity:
- The displacement s can be expressed as:
s=ut+12at2
Again, since u=0:
s=12at2
4. Expressing Time in Terms of Velocity:
- From the equation v=at, we can express time t in terms of velocity v:
t=va
5. Substituting Time into Displacement Equation:
- Now, substitute t into the displacement equation:
s=12a(va)2
Simplifying this gives:
s=12a⋅v2a2=v22a
6. Identifying the Graph:
- The relationship s=12av2 indicates that displacement s is proportional to the square of the velocity v. This is a parabolic relationship, which means the graph of displacement versus velocity will be a parabola opening upwards.
Conclusion:
The displacement (s) - velocity (v) graph of the particle is a parabola that opens upwards.
- The particle starts from rest, which means at time t=0, the initial velocity v0=0 and the initial displacement s0=0.
- Since the particle is moving with uniform acceleration a, the equations of motion can be applied. The velocity v at any time t can be expressed as:
v=u+at
where u=0 (initial velocity). Thus, we have:
v=at
- The displacement s can be expressed as:
s=ut+12at2
Again, since u=0:
s=12at2
- From the equation v=at, we can express time t in terms of velocity v:
t=va
- Now, substitute t into the displacement equation:
s=12a(va)2
Simplifying this gives:
s=12a⋅v2a2=v22a
- The relationship s=12av2 indicates that displacement s is proportional to the square of the velocity v. This is a parabolic relationship, which means the graph of displacement versus velocity will be a parabola opening upwards.
The displacement (s) - velocity (v) graph of the particle is a parabola that opens upwards.
Similar Questions
An object is moving with a uniform acceleration which is parallel to its instantaneous direction of motion. The displacement velocity (v) graph of this object is
View SolutionAn object is moving with a uniform acceleration which is parallel to its instantaneous direction of motion. The dispalcement (s)-velocity (v) graph of this object is.
View Solution
Knowledge Check
A particle starts from rest with uniform acceleration and its velocity after n seconds is v. The displacement of the body in last two seconds is.
A2v(n - 1)/nBv(n - 1)/nCv(n + 1)/nD2v(n + 1)/n
An object is moving with a uniform acceleration which is parallel to its instantaneous direction of motion. The dispalcement (s)-velocity (v) graph of this object is.
View SolutionA body starts from rest and then moves with uniform acceleration. Then.
View SolutionThe graph between displacement and time for a particle moving with uniform acceleration is a
View SolutionThe figure shows the v−t graph of a particle moving in a straight line. Starting from rest, the time after which the particle returns to its starting position is

View SolutionA particle of mass M starting from rest undergoes uniform acceleration. If the speed acquired in time T is V, the power delivered to the particle is -
View SolutionA particle starts from rest and moves with constant acceleration. Then velocity displacement curve is:
View SolutionA body starting from rest is moving with a uniform acceleration of 8ms2. Then the distance travelled by it in 5th second will be
View Solution
