Question

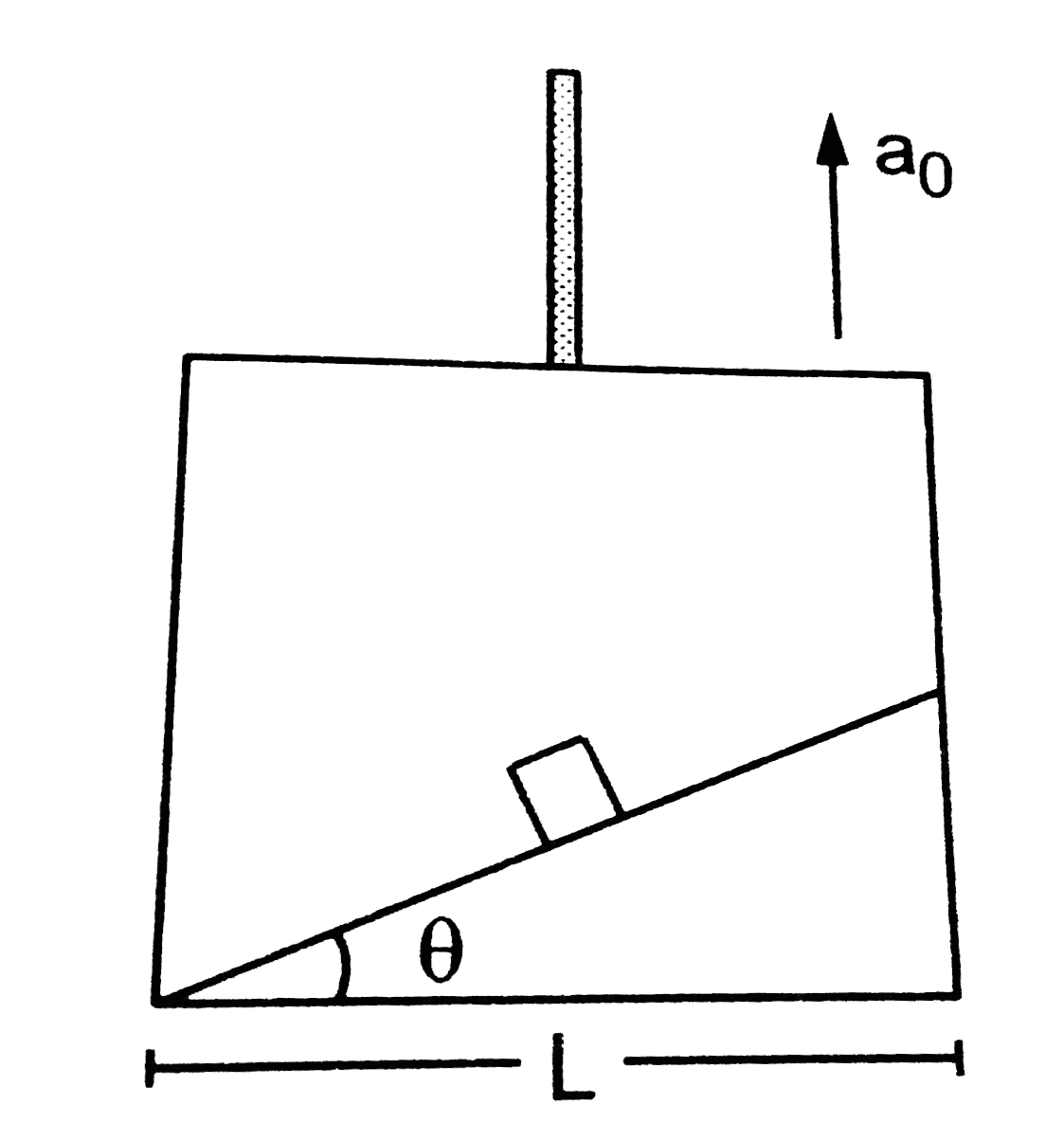
A body of mass ${\displaystyle m}$ is placed over a smooth inclined plane of inclination ${\displaystyle \theta }$. Which iis placed over a lift which is moving up with an acceleration ${\displaystyle a_0}$ . Base length o f the inclined plane is ${\displaystyle L}$ . Calculate the velocity of the block with respect to lift at the bottom, if it is allowed to slide down from the top of the plane from rest.

Options

A. `sqrt(2(a_0+g)Lsintheta)`
B. `sqrt(2(a_0+g)Lcostheta)`
C. `sqrt(2(a_0+g)Ltantheta)`
D. `sqrt(2(a_0+g)Lcottheta)`

Answer

C

Explanation

To solve the problem, we will follow these steps:

Step 1: Understand the Forces Acting on the Block
The block of mass `m` is on a smooth inclined plane with an angle of inclination `theta`. The lift is moving upwards with an acceleration `a_0`. The forces acting on the block are:
- The gravitational force `mg` acting downwards.
- A pseudo force `ma_0` acting downwards due to the acceleration of the lift.

Step 2: Calculate the Net Acceleration of the Block
The effective acceleration acting on the block along the incline can be calculated by resolving the forces:
- The component of gravitational force acting down the incline: \( mg \sin \theta \)
- The component of the pseudo force acting down the incline: \( ma_0 \sin \theta \)

Thus, the net acceleration \( A \) of the block down the incline is given by:
\( A = g \sin \theta + a_0 \sin \theta = (g + a_0) \sin \theta \)

Step 3: Determine the Displacement Along the Incline
The base length of the inclined plane is given as `L`. To find the height `h` of the incline, we can use the relationship:
\( h = L \tan \theta \)
The displacement along the incline \( S \) can be calculated using the cosine of the angle:
\( S = \frac{L}{\cos \theta} \)

Step 4: Use the Kinematic Equation to Find the Final Velocity
Since the block starts from rest, we can use the kinematic equation:
\( v^2 = u^2 + 2AS \)
Where:
- \( u = 0 \) (initial velocity)
- \( A = (g + a_0) \sin \theta \)
- \( S = L \)

Substituting these values into the equation gives:
\( v^2 = 0 + 2(g + a_0) \sin \theta \cdot L \)
Thus,
\( v = \sqrt{2(g + a_0) \sin \theta \cdot L} \)

Step 5: Final Expression for Velocity with Respect to the Lift
Since we need the velocity of the block with respect to the lift, we can conclude that the final velocity of the block as it reaches the bottom of the incline is:
\( v = \sqrt{2(g + a_0) L \sin \theta} \)

Summary of the Solution
The velocity of the block with respect to the lift at the bottom of the inclined plane is:
\( v = \sqrt{2(g + a_0) L \sin \theta} \)