A body is released from the top of a smooth inclined plane of inclination θ. It reaches the bottom with velocity v. If the angle of inclina-tion is doubled for the same length of the plane, what will be the velocity of the body on reach ing the ground .
v
2v
[2cosθ]1/2v
[2sinθ]1/2v
The correct Answer is:C
To solve the problem step by step, we can follow these steps:
Step 1: Understand the problem
We have a body released from the top of a smooth inclined plane with an angle of inclination θ. It reaches the bottom with a velocity v. We need to find the velocity when the angle of inclination is doubled to 2θ while keeping the length of the incline the same.
Step 2: Analyze the first scenario (angle θ)
Using the equation of motion, we know that:
v2=u2+2as
where:
- u=0 (initial velocity)
- a=gsinθ (acceleration down the incline)
- s is the length of the incline.
Substituting these values, we get:
v2=0+2(gsinθ)s
Thus, we can write:
v2=2gssinθ
Step 3: Analyze the second scenario (angle 2θ)
For the second scenario where the angle is 2θ, the acceleration down the incline becomes:
a′=gsin(2θ)
Using the double angle identity, we can express sin(2θ) as:
sin(2θ)=2sinθcosθ
Now, substituting this into the equation of motion:
v′2=u2+2a′s
Again, u=0, so:
v′2=0+2(gsin(2θ))s
Substituting for sin(2θ):
v′2=2g(2sinθcosθ)s
This simplifies to:
v′2=4gssinθcosθ
Step 4: Relate v′ to v
From the first scenario, we know:
v2=2gssinθ
Now, substituting this into the equation for v′:
v′2=4⋅v22⋅cosθ=2v2cosθ
Taking the square root gives:
v′=√2v2cosθ=v√2cosθ
Final Answer
Thus, the velocity of the body when the angle of inclination is doubled is:
v′=v√2cosθ
We have a body released from the top of a smooth inclined plane with an angle of inclination θ. It reaches the bottom with a velocity v. We need to find the velocity when the angle of inclination is doubled to 2θ while keeping the length of the incline the same.
Using the equation of motion, we know that:
v2=u2+2as
where:
- u=0 (initial velocity)
- a=gsinθ (acceleration down the incline)
- s is the length of the incline.
v2=0+2(gsinθ)s
Thus, we can write:
v2=2gssinθ
For the second scenario where the angle is 2θ, the acceleration down the incline becomes:
a′=gsin(2θ)
Using the double angle identity, we can express sin(2θ) as:
sin(2θ)=2sinθcosθ
Now, substituting this into the equation of motion:
v′2=u2+2a′s
Again, u=0, so:
v′2=0+2(gsin(2θ))s
Substituting for sin(2θ):
v′2=2g(2sinθcosθ)s
This simplifies to:
v′2=4gssinθcosθ
From the first scenario, we know:
v2=2gssinθ
Now, substituting this into the equation for v′:
v′2=4⋅v22⋅cosθ=2v2cosθ
Taking the square root gives:
v′=√2v2cosθ=v√2cosθ
Thus, the velocity of the body when the angle of inclination is doubled is:
v′=v√2cosθ
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - EXERCISE-340videos
MOTION IN A PALNE
- BOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - SOLVED EXAMPLE28videos
MOTION IN A PALNE
- BOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - EXERCISE-199videos
MOTION IN A PALNE
- BOOK - ALLENCHAPTER - KINEMATICS-2DEXERCISE - Exercise (O-2)46videos
KINEMATICS-2D
- BOOK - ALLENCHAPTER - NEWTON'S LAWS OF MOTION & FRICTIONEXERCISE - EXERCISE (JA)4videos
NEWTON'S LAWS OF MOTION & FRICTION
Similar Questions
A body is kept on a smooth inclined plane having an inclination of 1 in x. Then,
View SolutionA block is released from the top of a smooth inclined plane of inclination θ as shown in figure. Let υ be the speed of the particle after travelling a distance s down the plane. Then which of the following will remain constant ?
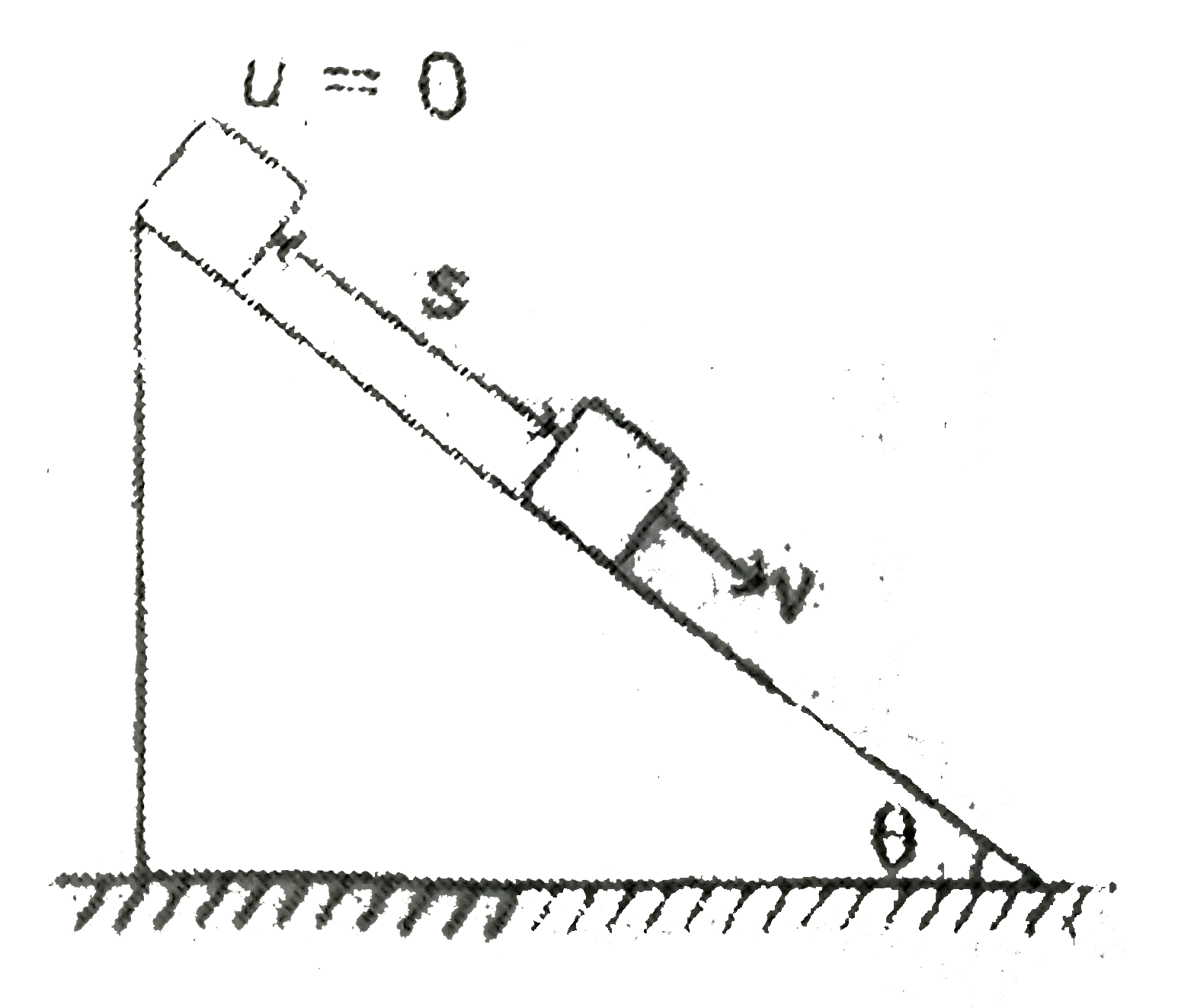 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
An object of mass m is released from rest from the top of a smooth inclined plane of height h. Its speed at the bottom of the plane is proportional to
Am0BmCm2Dm−1 - Question 2 - Select One
A block released from rest from the top of a smooth inclined plane of angle θ1 reaches the bottom in time t1. The same block released from rest from the top of another smooth inclined plane of angle θ2 reaches the bottom in time t2 If the two inclined planes have the same height, the relation between t1andt2 is
At2t1=(sinθ1sinθ2)1/2Bt2t1=1Ct2t1=sinθ1sinθ2Dt2t1=sin2θ1sin2θ2
A block released from rest from the tope of a smooth inclined plane of angle of inclination θ1=30∘ reaches the bottom in time t1. The same block, released from rest from the top of another smooth inclined plane of angle of inclination θ2=45∘ reaches the bottom in time t2. Time t1 and t2 are related as ( Assume that the initial heights of blocks in the two cases are equal ).
View SolutionAn object is placed on the surface of a smooth inclined plane of inclination θ . It takes time t to reach the bottom of the inclined plane. If the same object is allowed to slide down rough inclined plane of same inclination θ, it takes time nt to reach the bottom where n is a number greater than 1. The coefficient of friction μ is given by -
View SolutionA body weighs 64 N on the surface of the Earth. What is the gravitational force on it (in N) due to the Earth at a height equal to one-third of the radius of the Earth?
View SolutionA body of mass m is placed over a smooth inclined plane of inclination θ. Which iis placed over a lift which is moving up with an acceleration a0 . Base length o f the inclined plane is L . Calculate the velocity of the block with respect to lift at the bottom, if it is allowed to slide down from the top of the plane from rest.
View SolutionA body of mass m slides down an incline and reaches the bottom with a velocity v. If the same mass were in the form of a ring which rolls down this incline, the velocity of the ring at the bottom would have been
View SolutionA block is kept on an inclined plane of inclination θ of length l. the velocity of particle at the bottom of inclined is (the coefficient of friciton is μ)
View Solution

