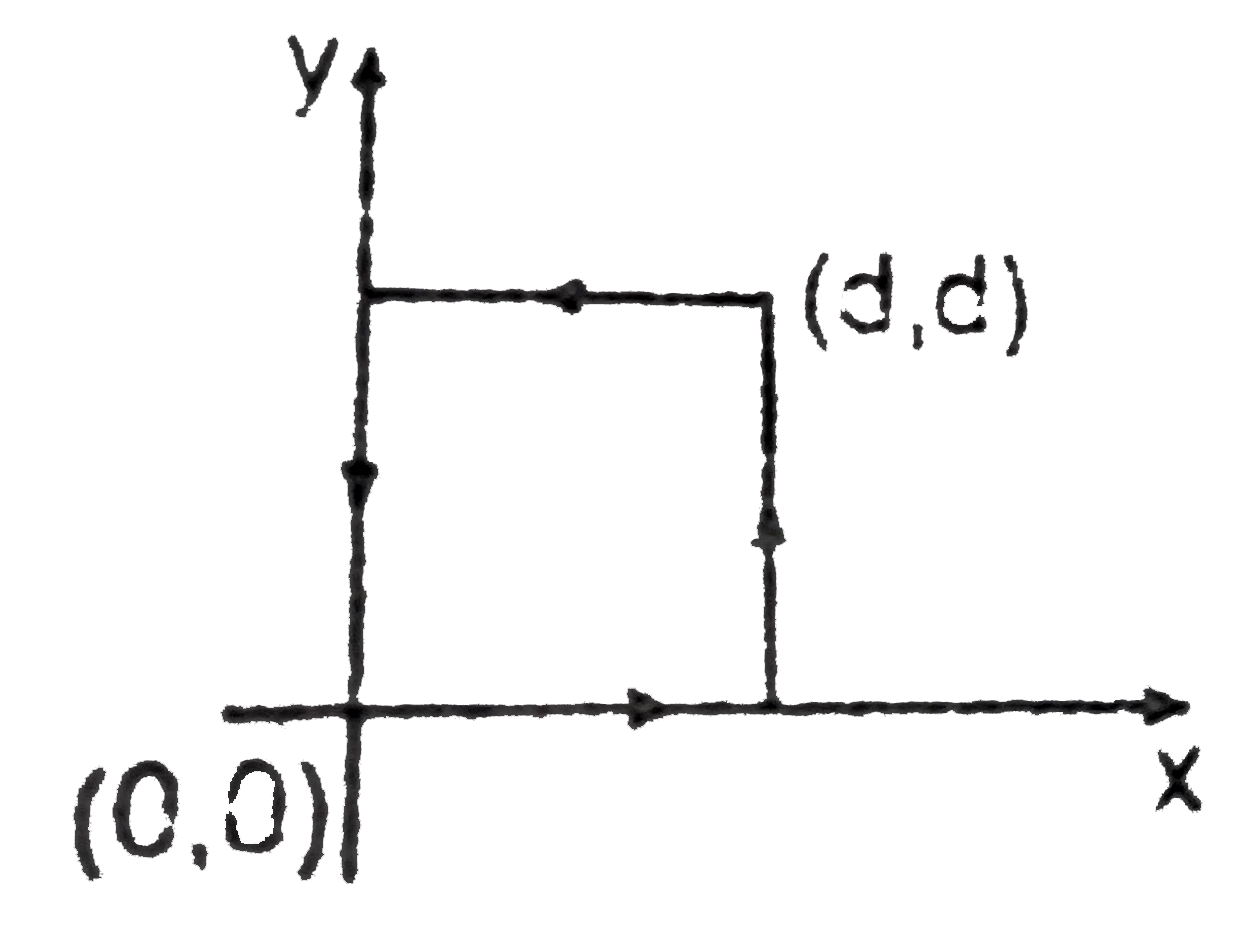
The work done by the force F=A(y2ˆi+2x2ˆj), where A is a constant and x & y are in meters around the path shown in
zero
Ad
Ad2
Ad3
The correct Answer is:D
∫→Fd→x=∫A(y2ˆi+2x2ˆj)(dxˆi+dyˆj)
A∫(y2dx+2x2dy)
WOA=0+0,WAB=A[0+2d2d]
WBC=A[d2(−d)+0],WCD=A[0+0]
W=0+2Ad3−Ad3+0=Ad3
Similar Questions
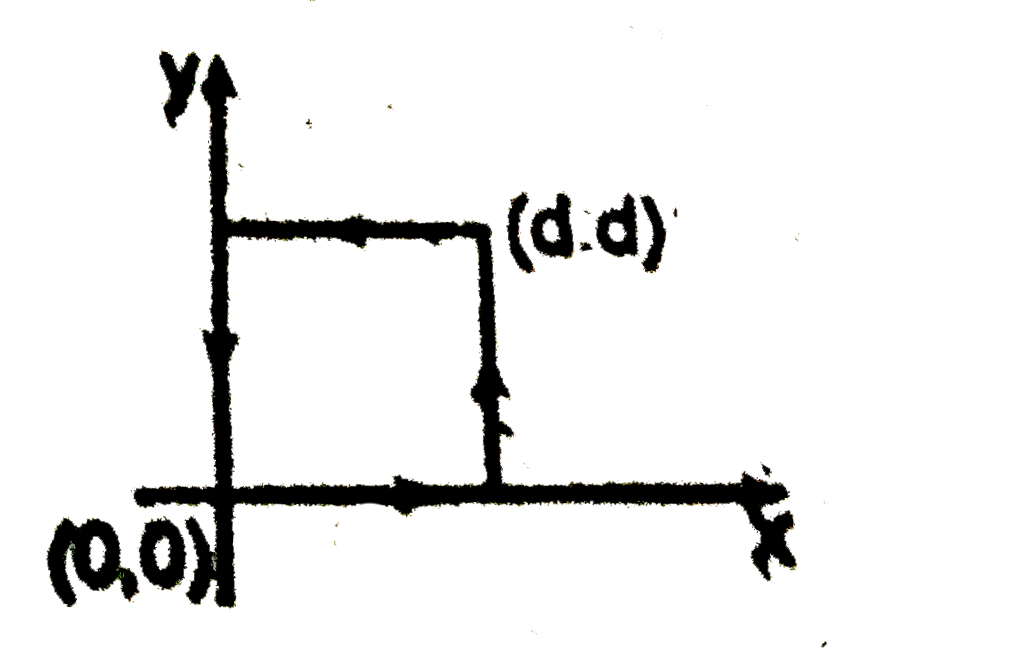
The work done by the force →F=A(y2ˆi+2x2ˆj), where A is a constant and x & y are in meters around the path shown is :
 View Solution
View SolutionThe work done by the force F=A(y2ˆi+2x2ˆj), where A is a constant and x & y are in meters around the path shown in
 View Solution
View SolutionA particle is moving with velocity →v=k(yˆi+xˆj), where k is a constant . The genergal equation for its path is
View SolutionA particle is moving with velocity →v=k(yˆi+xˆj), where k is a constant . The genergal equation for its path is
View SolutionA particle is moving with velocity →v=k(yˆi+xˆj), where k is a constant . The genergal equation for its path is
View SolutionA body of mass 1 kg begins to move under the action of a time dependent force F=(2tˆi+3t2ˆj)N,whereˆiandˆj are unit vector along x and y axis. What power will be developed by the force at the time?
View SolutionIf →E=2x2ˆi−3y2ˆj, then V (x, y, z)
View SolutionA body of mass 1kg begins to move under the action of a time dependent force →F=(2tˆi+3t2ˆj)N, where ˆi and ˆj are unit vectors along x-and y-axes. What power will be developed by the force at the time t ?
View SolutionThe work done by a force →F=(−6x3ˆi) N in displacing a particle from x = 4m to x = - 2m is
View SolutionA force →F=(−yˆi+xˆj)N acts on a particle as it moves in an anticlockwise circular motion in x-y plane. The centre of the circle is at the origin. If the work done by the force is 32πJ in one complete revolution then asSigmaing x,y to be in meters, find the radius of the path.
View Solution

