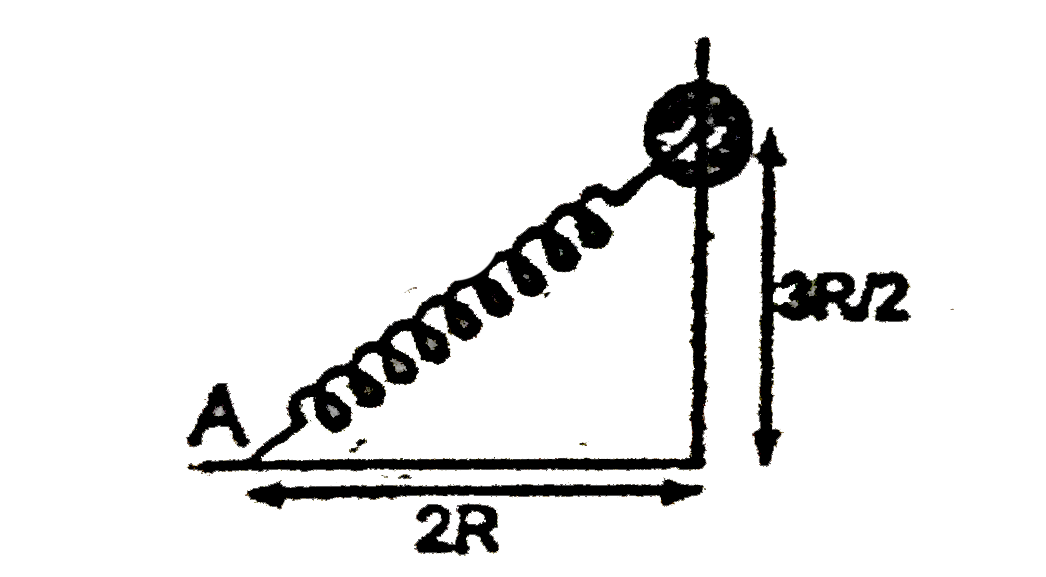
A ring of mass m can slide over a smooth vertical rod. The ring is connected to a spring of force constant K=4mgR where 2R is the natural length of the spring. The other end spring is fixed to the ground at a horizontal distance 2R from the base of the rod. the mass is released at a height of 1.5 R from ground.
mgR2
3mgR2
3mgR5
mgR
The correct Answer is:A
AC=√(2R)2+(32R)2=52R
Extension in length of spring (x)=52R=2R=R2
Work done by spring =12kx2
=12(4mgR)(R24)=mgR2
Similar Questions
A ring of mass m can slide over a smooth vertical rod as shown in figure. The ring is connected to a spring of force constant k=4mg/R, where 2R is the natural length of the spring . The other end of spring is fixed to the ground at a horizontal distance 2R from base of the rod . If the mass is released at a height 1.5J then the velocity of the ring as it reaches the ground is

View SolutionA ring of mass m=10kg can slide through a vertical rod with friction. It is connected with a spring of force constant k=100Nm−1. The relaxed length of spring is 4m. The ring is displaced 3m as shown in the figure and released. Find velocity of ring when spring becomes horizontal.
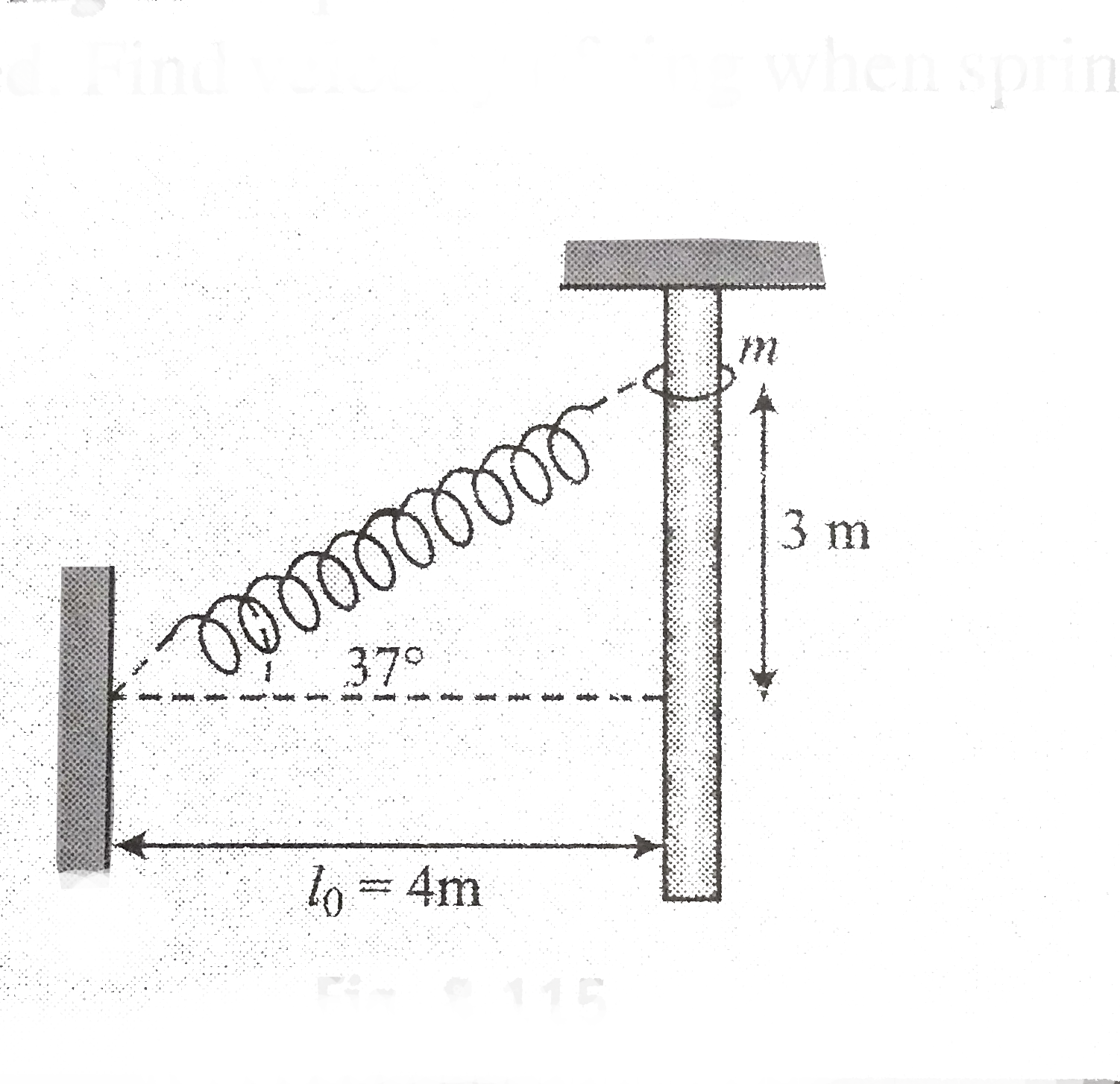
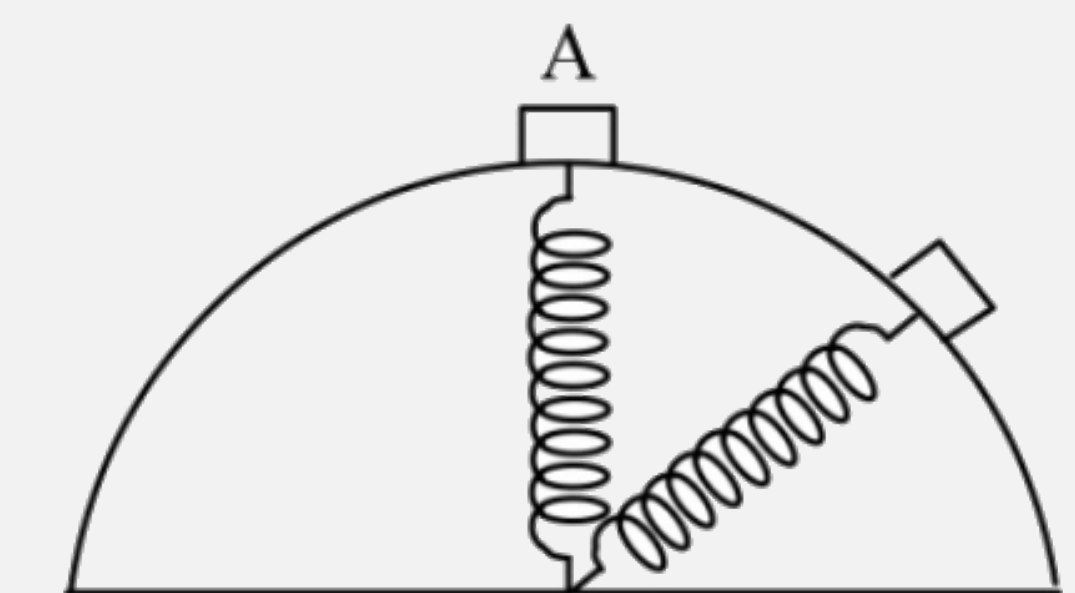
View SolutionA bead of mass m can slide without friction along a vertical ring of radius R. One end of a spring of force constant k=3mgR is connected to the bead and the other end is fixed at the centre of the ring. Initially, the bead is at the point A and due to a small push it starts sliding down the ring. If the bead momentarily loses contact with the ring at the instant when the spring makes an angle 60∘ with the vertical, then the natural length of the spring is
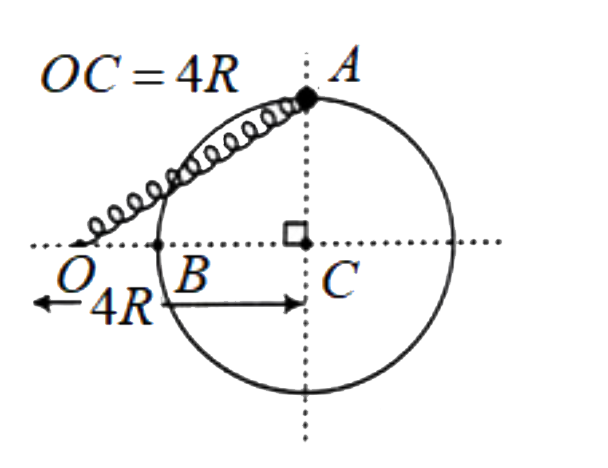
View SolutionA bead of mass m can slide without friction on a fixed circular horizontal ring of radius 3R having a centre at the point C. The bead is attached to one of the ends of spring of spring constant k. Natural length of spring is R and the other end of the spring is R and the other end of the spring is fixed at point O as shown in the figure. If the bead is released from position A, then the kinetic energy of the bead when it reaches point B is
View Solution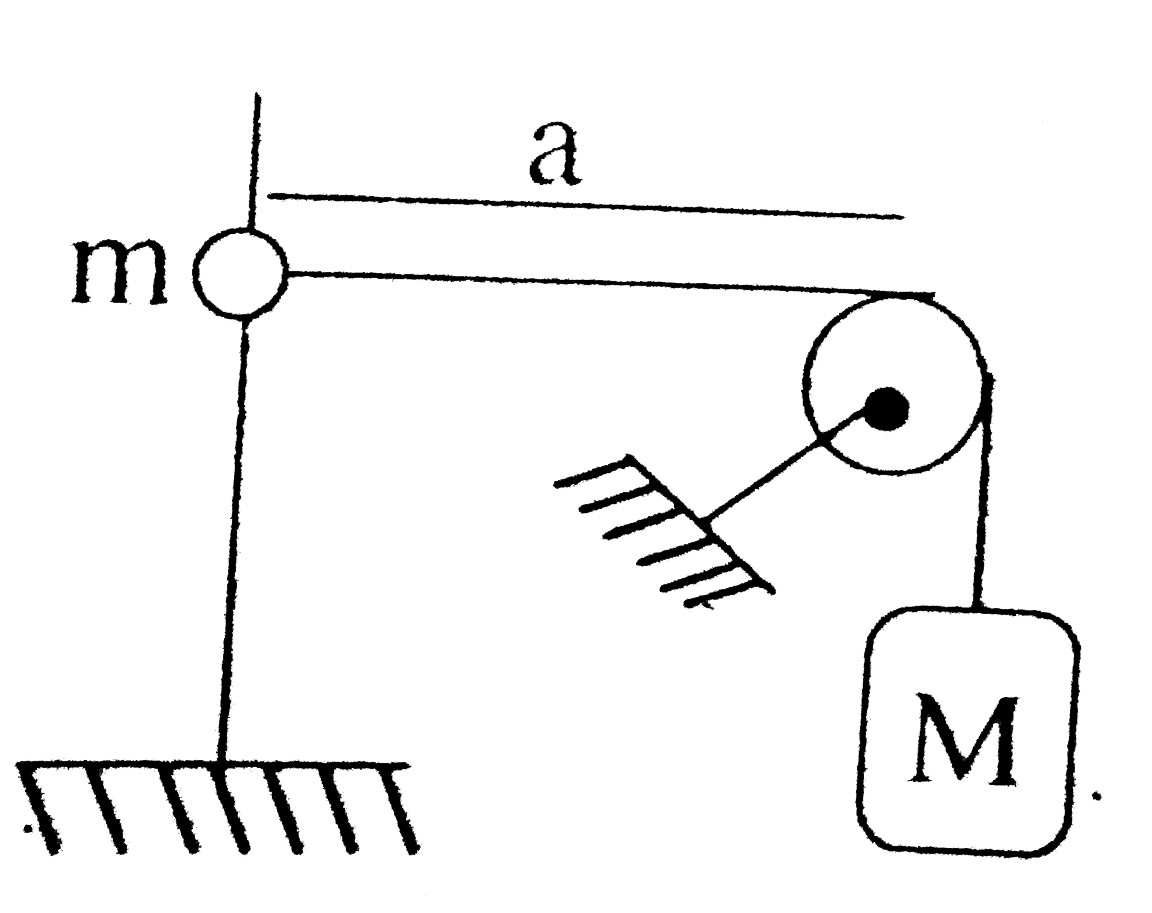
A ring of mass m can slide on the vertical smooth rod. Ring is connected by block with string as shown in figure. Pulley is of mass-less and smooth the system is released from reast. Initial tension in string is
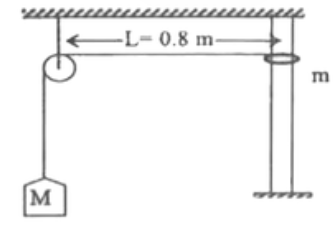
View SolutionA ring of mass m = 0.3kg can slide freely on smooth vertical rod. A light and inextensible string is connected to the ring and passes over a smooth and fixed pulley as shown in the figure. The distance of the pulley from the rod is 0.8m and the other end of the string is connected to a block of mass M = 0.5kg. The ring is held in level with pulley and then released from rest.
The distance by which the ring moves down before coming to rest for the first time is 0.75K. Find K.
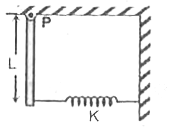
View SolutionA straight rod of light L and mass m is pivoted freely from a point of the roof. Its lower end is connected to an ideal spring of spring constant K. The other end of the spring is connected to the wall as shown in the figure. Find the frequency of small oscillation of the system.
View Solution
A small block of mass m is fixed at upper end of a massive vertical spring of spring constant k=2mgL and natural length 10L The lower end of spring is free and is at a height L from fixed horizontal floor as shown. The spring is initially unstressed and the spring block system is released from rest in the shown position.
Q. At the instant the speed of block is maximum the magitude of force exeted by the spring on the block is
View Solution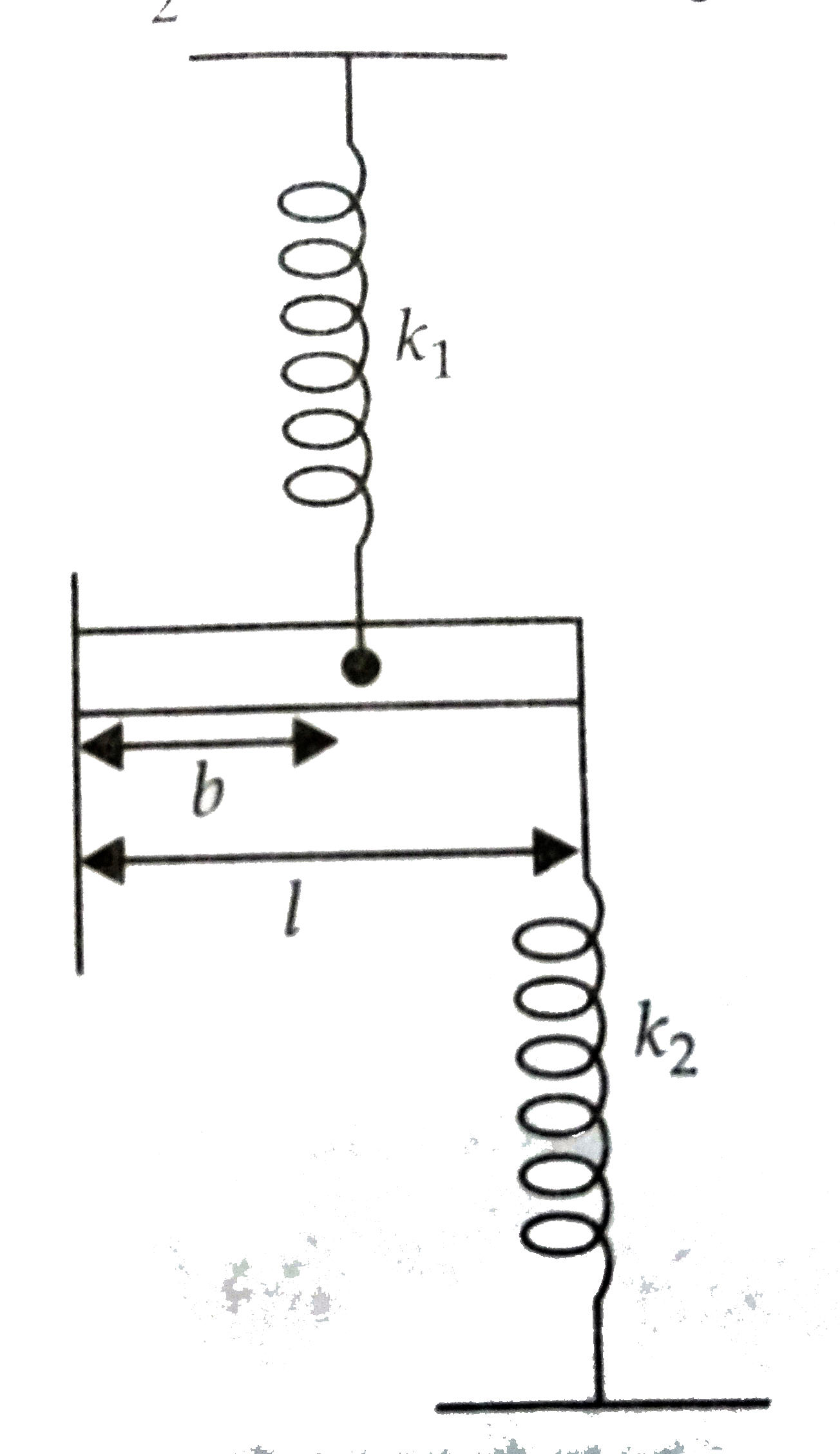
A rod of mass m and length l is connected by two spring of spring constants k1andk2, so that it is horizontal at equilibrium. What is the natural frequency of the system?
View Solution
A small block of mass m is fixed at upper end of a massive vertical spring of spring constant k=2mgL and natural length 10L The lower end of spring is free and is at a height L from fixed horizontal floor as shown. The spring is initially unstressed and the spring block system is released from rest in the shown position.
Q. Till the blocks reaches its lowest position for the first time, the time duration for which the spring remains compressed is
View Solution
