A bead of mass m can slide without friction along a vertical ring of radius R. One end of a spring of force constant k=3mgR is connected to the bead and the other end is fixed at the centre of the ring. Initially, the bead is at the point A and due to a small push it starts sliding down the ring. If the bead momentarily loses contact with the ring at the instant when the spring makes an angle 60∘ with the vertical, then the natural length of the spring is
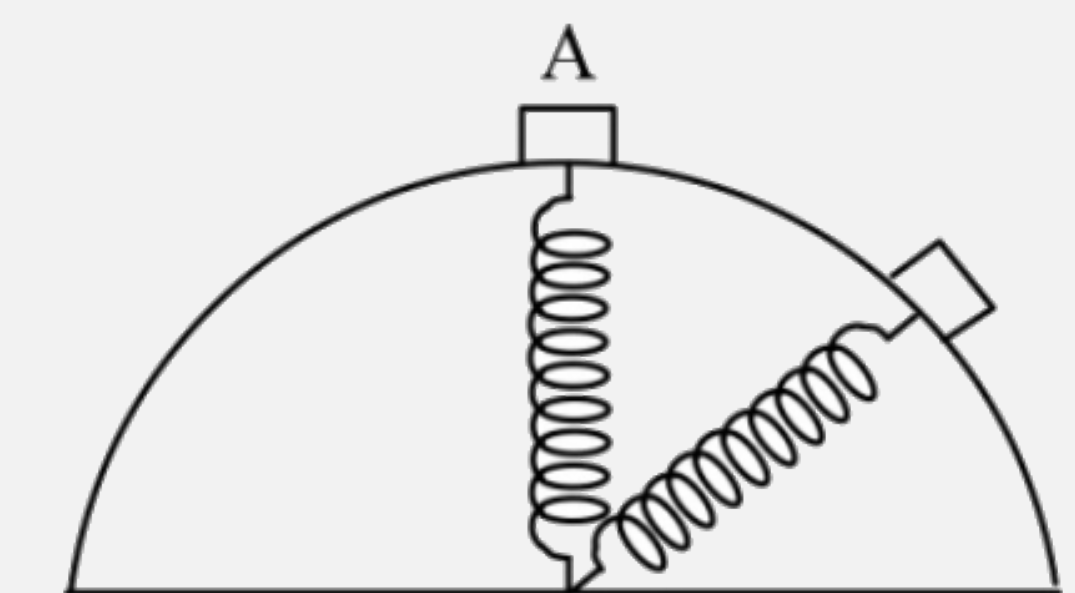
5R9
3R4
5R6
4R7
The correct Answer is:C
Step by step video & image solution for A bead of mass m can slide without friction along a vertical ring of radius R. One end of a spring of force constant k=(3mg)/(R ) is connected to the bead and the other end is fixed at the centre of the ring. Initially, the bead is at the point A and due to a small push it starts sliding down the ring. If the bead momentarily loses contact with the ring at the instant when the spring makes an angle 60^(@) with the vertical, then the natural length of the spring is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
A ring of mass m can slide over a smooth vertical rod. The ring is connected to a spring of force constant K=4mgR where 2R is the natural length of the spring. The other end spring is fixed to the ground at a horizontal distance 2R from the base of the rod. the mass is released at a height of 1.5 R from ground.
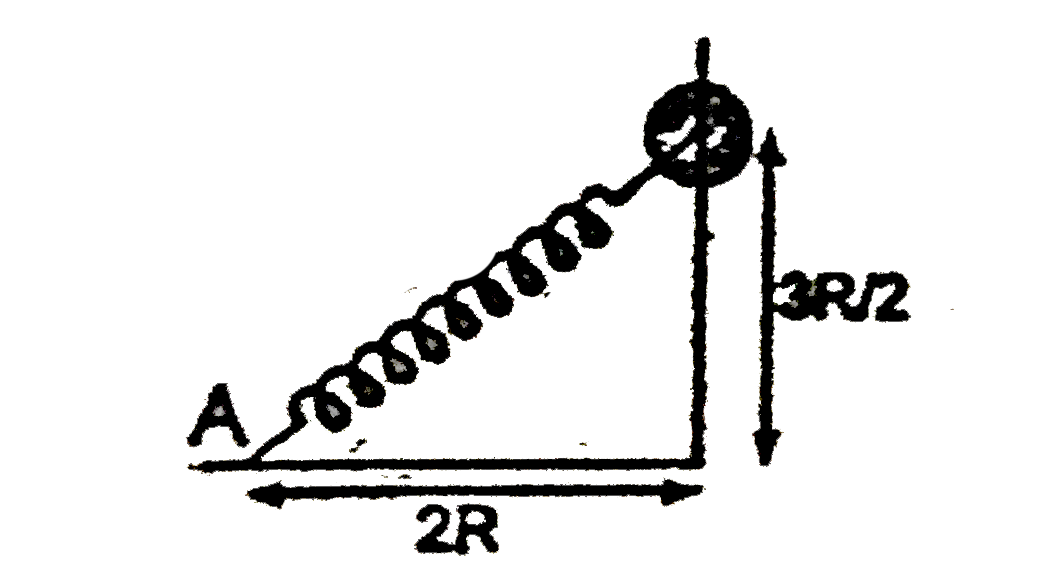
View SolutionA ring of mass m can slide over a smooth vertical rod. The ring is connected to a spring of force constant K=4mgR where 2R is the natural length of the spring. The other end spring is fixed to the ground at a horizontal distance 2R from the base of the rod. the mass is released at a height of 1.5 R from ground.

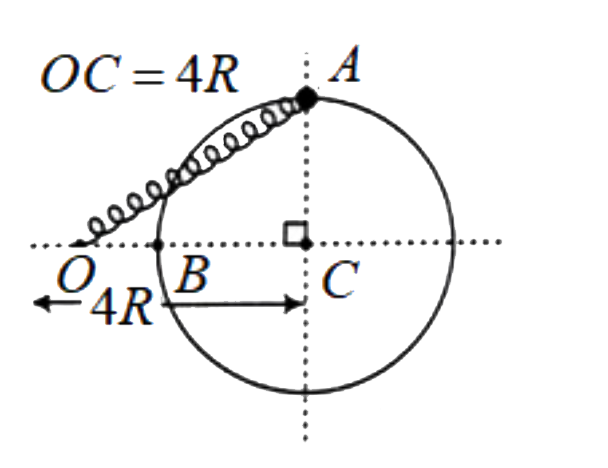
View SolutionA bead of mass m can slide without friction on a fixed circular horizontal ring of radius 3R having a centre at the point C. The bead is attached to one of the ends of spring of spring constant k. Natural length of spring is R and the other end of the spring is R and the other end of the spring is fixed at point O as shown in the figure. If the bead is released from position A, then the kinetic energy of the bead when it reaches point B is
View SolutionA ring of mass m can slide over a smooth vertical rod as shown in figure. The ring is connected to a spring of force constant k=4mg/R, where 2R is the natural length of the spring . The other end of spring is fixed to the ground at a horizontal distance 2R from base of the rod . If the mass is released at a height 1.5J then the velocity of the ring as it reaches the ground is

View SolutionA bead of mass m is attached to one end of a spring of natural length R and spring constant K=(√3+1)mgR. The other end of the spring is fixed at a point A on a smooth vertical ring of radius R as shown in fig. The normal reaction at B just after it is released to move is
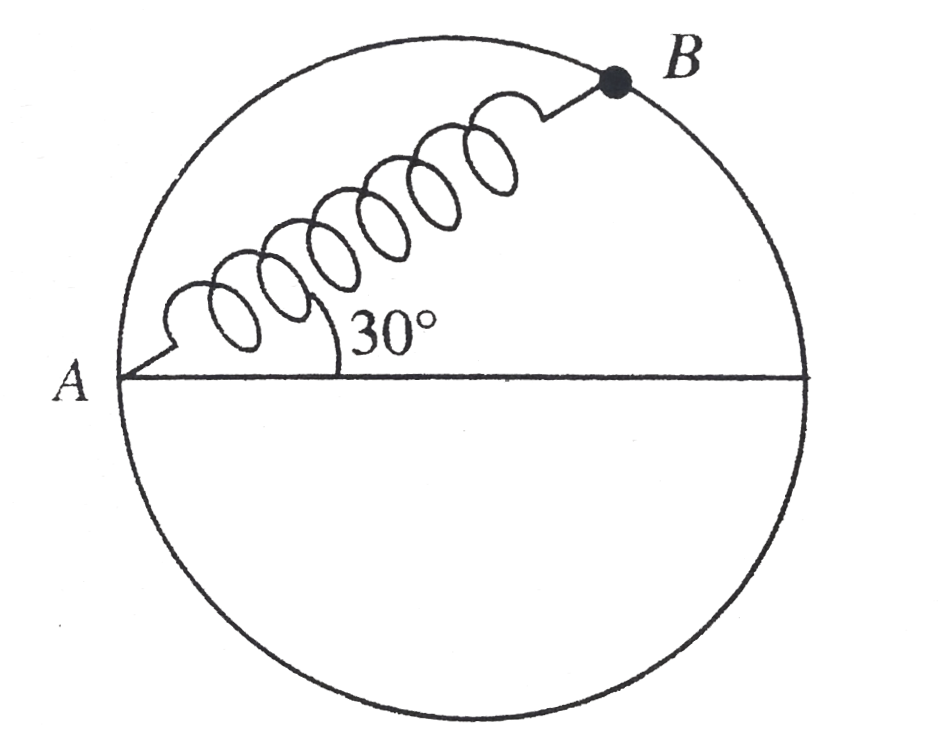
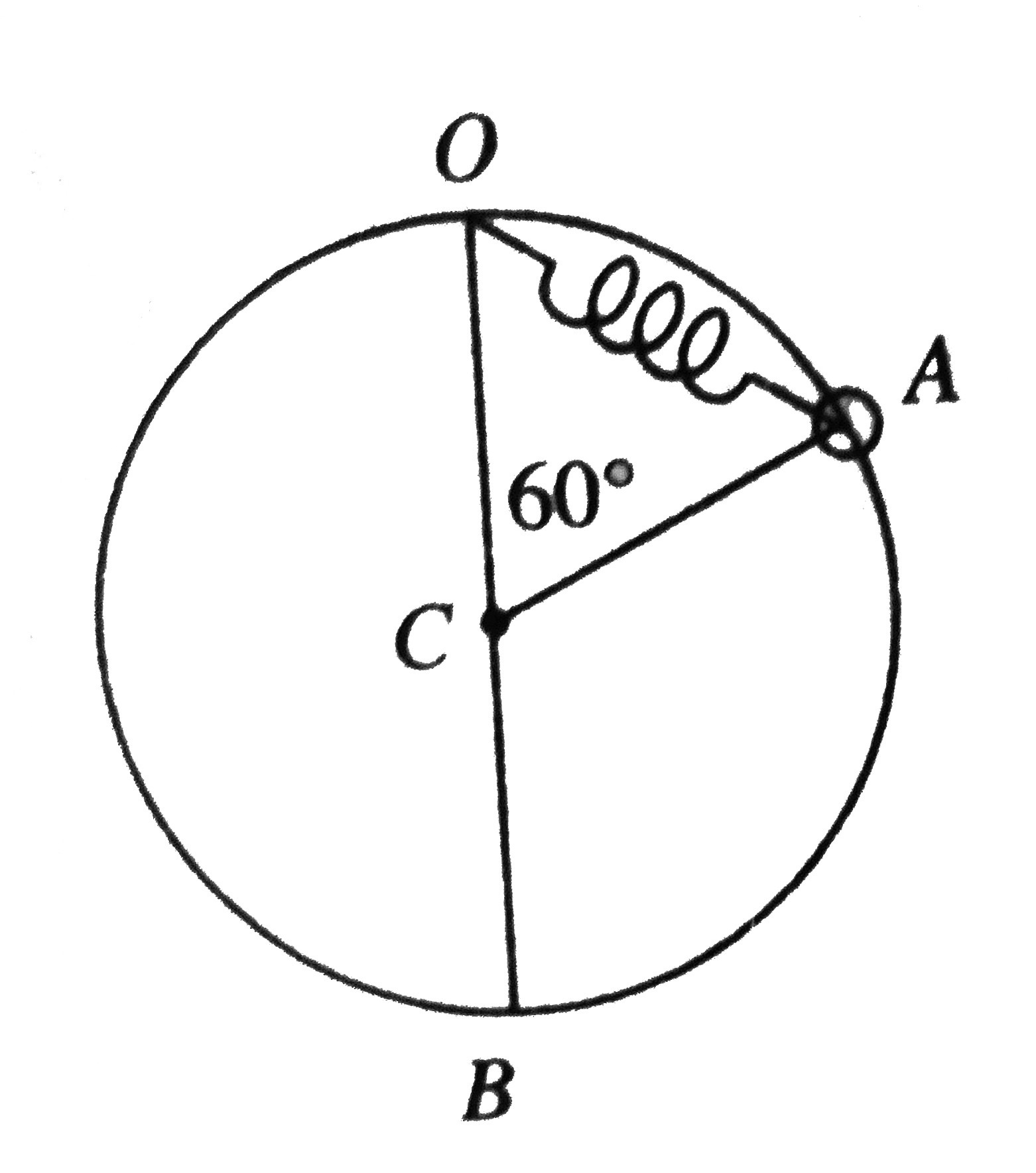
View SolutionA particle of mass 5kg is free to slide on a smooth ring of radius r=20cm fixed in a vertical plane. The particle is attached to one end of a spring whose other end is fixed to the top point O of the ring. Initially, the particle is at rest at a point A of the ring such that ∠OCA=60∘, C being the centre of the ring. The natural length of the spring is also equal to r=20cm. After the particle is released and slides down the ring, the contact force between the particle and the ring becomes zero when it reaches the lowest position B. Determine the force constant (in×102Nm−1) of the spring.
View SolutionA bead of mass m slides without friction on a vertical hoop of radius R. The bead moves under the combined influence of gravity and a spring of spring constant k attached to the bottom of the hoop. For simplicity assume, the equilibrium length of the spring to be zero. The bead is released at the top of the hoop with negligible speed as shown . The bead, on passing the bottom point will have a velocity of :
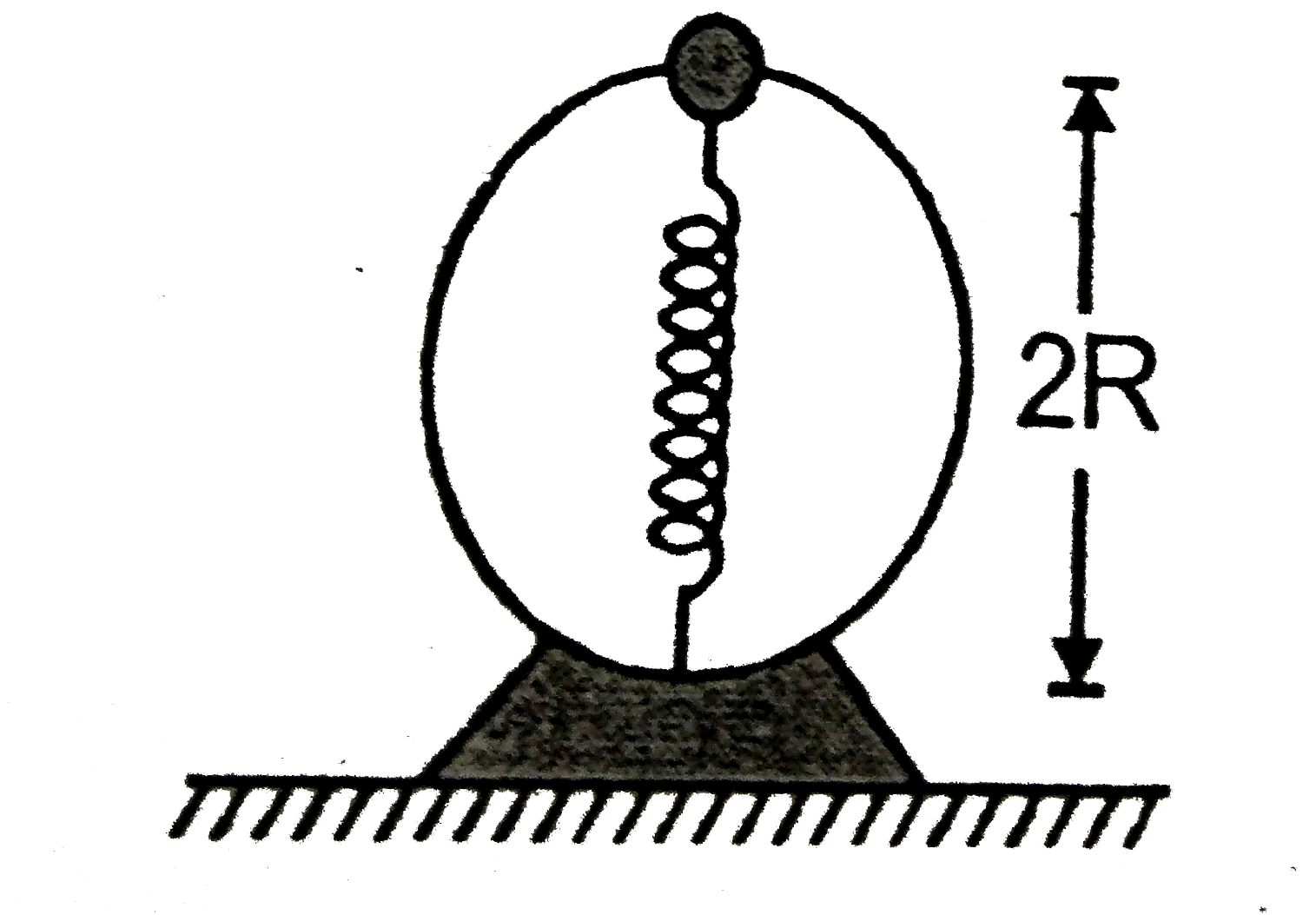
View SolutionAn underformed spring of spring constant k is connected to a bead of mass m which can move along a frictionless rod as shown in the figure. If the particle strikes the bead at an angle of 45∘ with the horizontal and sticks to it, then the maximum elongation of the spring after the collision is

View SolutionColour of the bead in borax bead testis mainly due to the formation of
View SolutionThe borax bead is due to formation of
View Solution
