A ring of mass m = 0.3kg can slide freely on smooth vertical rod. A light and inextensible string is connected to the ring and passes over a smooth and fixed pulley as shown in the figure. The distance of the pulley from the rod is 0.8m and the other end of the string is connected to a block of mass M = 0.5kg. The ring is held in level with pulley and then released from rest.
The distance by which the ring moves down before coming to rest for the first time is 0.75K. Find K.

The correct Answer is:2
Step by step video & image solution for A ring of mass m = 0.3kg can slide freely on smooth vertical rod. A light and inextensible string is connected to the ring and passes over a smooth and fixed pulley as shown in the figure. The distance of the pulley from the rod is 0.8m and the other end of the string is connected to a block of mass M = 0.5kg. The ring is held in level with pulley and then released from rest. The distance by which the ring moves down before coming to rest for the first time is 0.75K. Find K. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Three weights are hanging over a smooth fixed pulley as shown in the figure. What is the tension in the string connecting weights B and C ?
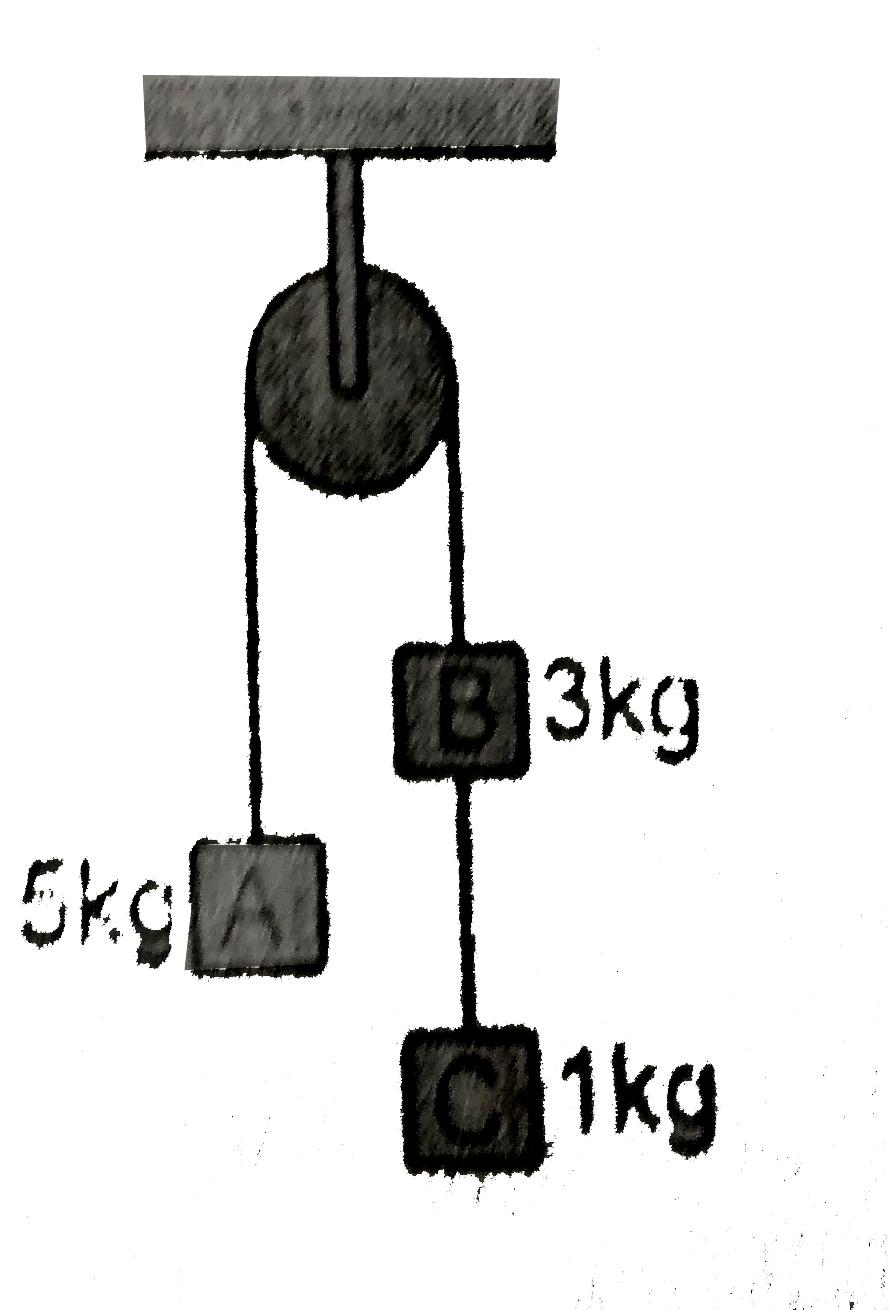
View SolutionA ring of mass m=1kg can slide over a smooth vertical rod. A light string attached to the ring passing over a smooth fixed pulley at a distance of L=0.7m from the rod as shown in figure.
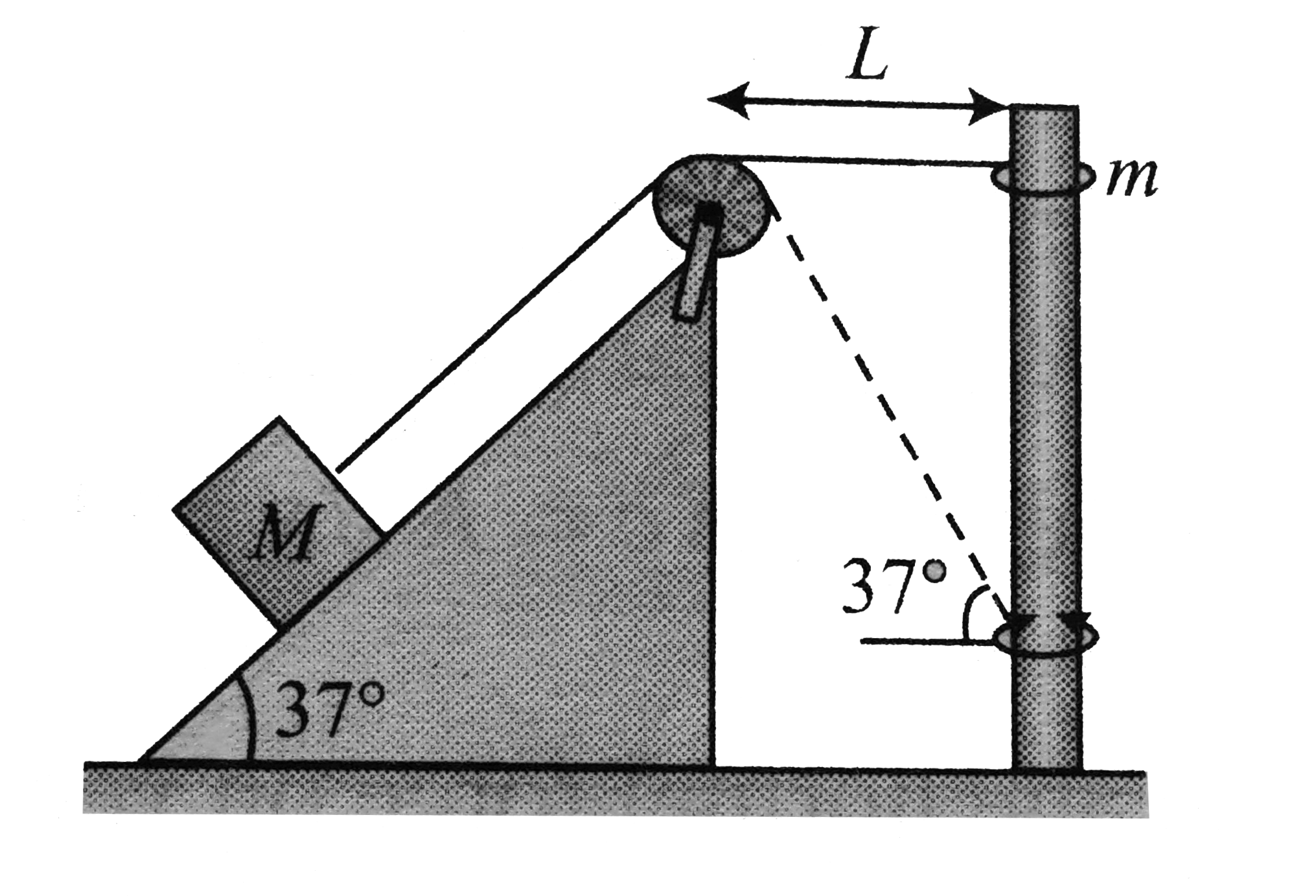
At the other end of the string mass M=5kg is attached, lying over a smooth fixed inclined plane of inclination angle 37∘. The ring is held in level with the pulley and released. Determine the velocity of ring when the string makes an angle (α=37∘) with the horizontal. [sin37∘=0.6]
View Solution
Knowledge Check
Two blocks of masses of 40 kg and 30 kg are connected by a weightless string passing over a frictionless pulley as shown in the figure.
 A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2
A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2A string of negligible mass going over a clamped pulley of mass m supports a block of M as shown in the figure. the force on the pulley by the clamp is given by:
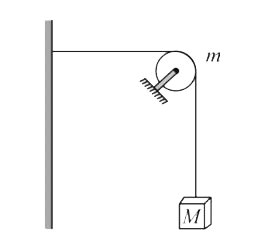 A√2MgB√2mgC√(M+m)2+m2gD√(M+m)2+M2g
A√2MgB√2mgC√(M+m)2+m2gD√(M+m)2+M2g
Two masses of 10 kg and 20 kg are connected with an inextensible string passing over two smooth pulleys as shown in the figure. The acceleration of 20 kg mass will be :
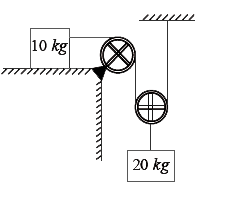
View SolutionTwo masses m and M(m<M) are joined by a light string passing over a smooth and light pulley (as shown)

View SolutionTwo blocks are connected by a long inextensible string passing over an ideal pulley as shown in the figure. If the system is released from rest then the common speed of blocks when block m2 moves a distance I will be
View SolutionA ring of mass m can slide over a smooth vertical rod as shown in figure. The ring is connected to a spring of force constant k=4mg/R, where 2R is the natural length of the spring . The other end of spring is fixed to the ground at a horizontal distance 2R from base of the rod . If the mass is released at a height 1.5J then the velocity of the ring as it reaches the ground is

View SolutionA string of negligible mass going over a clamped pulley of mass m supports a block of mass M as shown in the figure. The force on the pulley by the clamp is given by

View Solution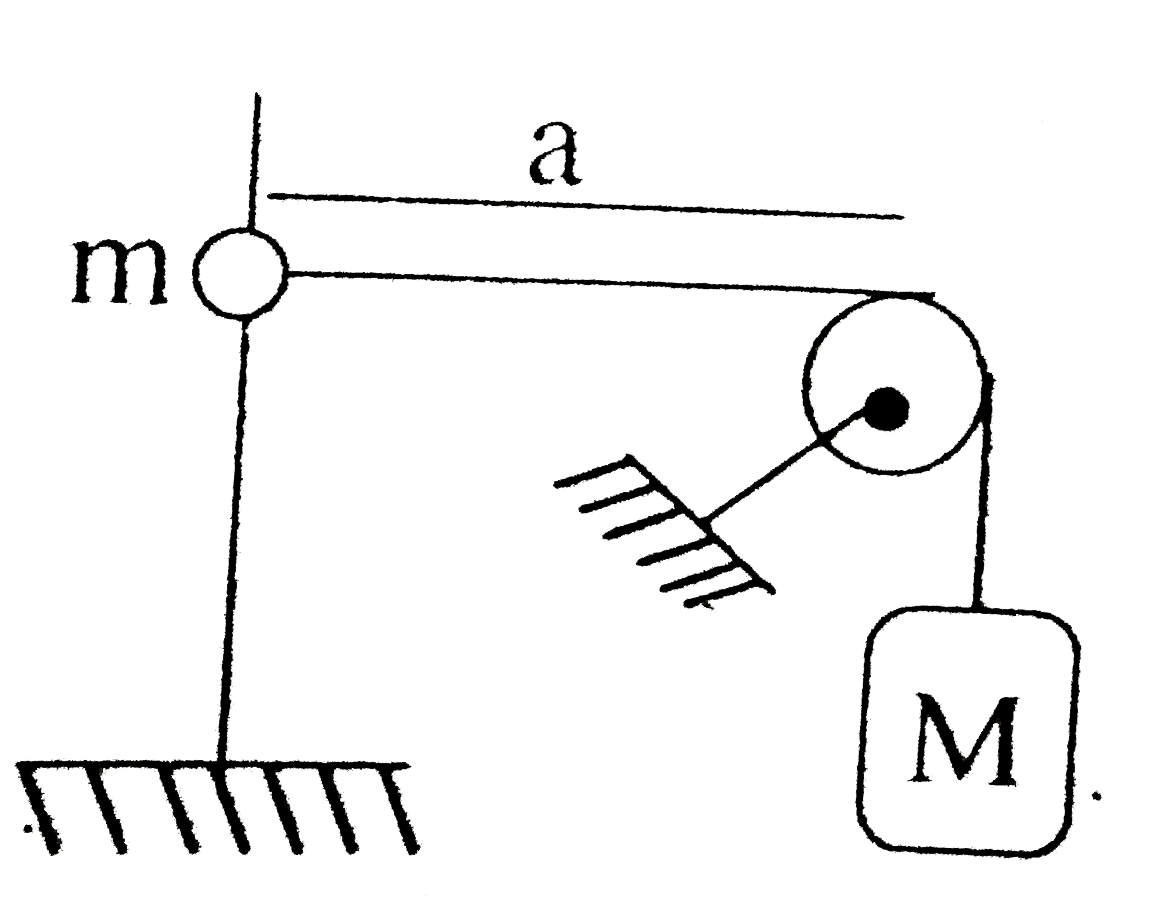
A ring of mass m can slide on the vertical smooth rod. Ring is connected by block with string as shown in figure. Pulley is of mass-less and smooth the system is released from reast. Initial tension in string is
View Solution
