An uncharged parallel plate capacitor is connected to a battery. The electric field between the plates is 10V/m. Now a dielectric of dielectric constant 2 is inserted between the plates filling the entries space. The electric field between the plates now is
5 V/m
20 V/m
10 V/m
none of these
The correct Answer is:C
To solve the problem, we need to understand how inserting a dielectric affects the electric field in a parallel plate capacitor. Here's the step-by-step solution:
Step 1: Understand the initial conditions
The initial electric field (E₀) between the plates of the capacitor is given as 10 V/m. The capacitor is connected to a battery, which means the voltage (V) across the plates remains constant.
Hint: Remember that the electric field (E) in a capacitor is related to the voltage (V) and the distance (d) between the plates by the formula E=Vd.
Step 2: Introduce the dielectric
When a dielectric material is inserted between the plates of the capacitor, it affects the electric field. The dielectric constant (κ) of the material is given as 2.
Hint: The dielectric constant reduces the electric field in the capacitor. The new electric field (E) can be calculated using the formula E=E0κ, where E0 is the initial electric field.
Step 3: Calculate the new electric field
Using the formula mentioned above:
E=E0κ=10V/m2=5V/m
Hint: Make sure to divide the initial electric field by the dielectric constant to find the new electric field.
Step 4: Conclusion
The electric field between the plates after inserting the dielectric is 5 V/m.
Final Answer
The electric field between the plates now is 5 V/m.
---
The initial electric field (E₀) between the plates of the capacitor is given as 10 V/m. The capacitor is connected to a battery, which means the voltage (V) across the plates remains constant.
When a dielectric material is inserted between the plates of the capacitor, it affects the electric field. The dielectric constant (κ) of the material is given as 2.
Using the formula mentioned above:
E=E0κ=10V/m2=5V/m
The electric field between the plates after inserting the dielectric is 5 V/m.
The electric field between the plates now is 5 V/m.
Similar Questions
A parallel plate capacitor is connected to a battery of emf V volts. Now a slab of dielectric constant k=2 is inserted between the plates of capacitor without disconnecting the battery. The electric field between the plates of capacitor after inserting the slab is E=PV2d. Find the value of P.
View SolutionA parallel plate capacitor is charged by a battery. After some time the battery is disconnected and a dielectric slab of dielectric constant K is inserted between the plates. How would (i) the capacitance, (ii) the electric field between the plates and (iii) the energy stored in the capacitor, be affected ? Justify your answer.
View SolutionA dielectric slab is inserted between the plates of an isolated capacitor. The force between the plates will
View SolutionWhen a dielectric slab is gradually inserted between the plates of an isolated parallel-plate capacitor , the energy of the system decreases.What can you conclude about the force on the slab exerted by the electric field?
View SolutionA parallel plate capacitor (without dielectric) is charged by a battery and kept connected to the battery. A dielectric salb of dielectric constant 'k' is inserted between the plates fully occupying the space between the plates. The energy density of electric field between the plates will:
View SolutionAnswer the following:
(a) When a parallel plate capacitor is connected across a dc battery, explain briefly how the capacitor gets charged.
(b) A parallel plate capacitor of capacitance 'C' is charged to 'V' volt by a battery. After some time the battery is disconnected and the distance between the plates is doubled. Now a slab of dielectric constant 1<k<2 is introduced to fill the space between the plates. How will the following be affected ?
(i) The electric field between the plates of the capacitor.
(ii) The energy stored in the capacitor. Justify your answer in each case.
(c) The electric potential as a function of distance 'x' is shown in the figure. Draw a graph of the electric field E as a function of x.
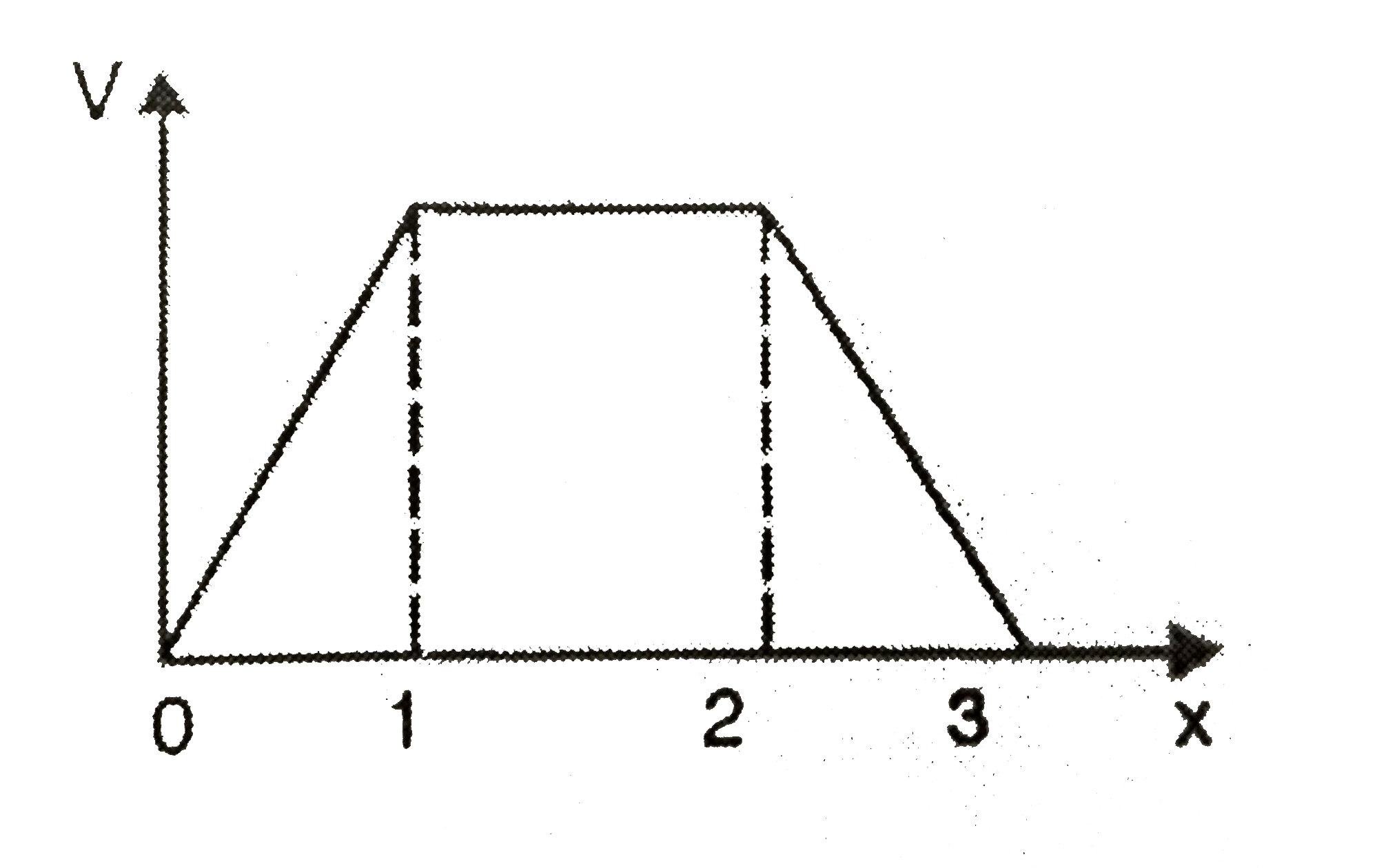
View SolutionA parallel plate capacitor of capacitance 90 pF is connected to a battery of emf 20 V. If a dielectric material of dielectric constant K=53 is inserted between the plates, the magnitude of the induced charge will be :
View SolutionA capacitor is connected to a battery of voltage V. Now a di-electric slab of di-electric constant k is completely inserted between the plates, then the final charge on the capacitor will be : (If initial charge is q0)
View SolutionTwo identical parallel plate capacitors are connected in series to a battery of 100V. A dielectric slab of dielectric constant 4.0 is inserted between the plates of second capacitor. The potential difference across the capacitors will now be respectively
View SolutionA parallel plate air capacitor has capacitance C. Half of space between the plates is filled with dielectric of dielectric constant K as shown in figure . The new capacitance is C . Then

View Solution