A 10μF capacitor and a 20μF capacitor are connected in series across a 200V supply line. The chraged capacitors are then disconnected from the line and reconnected with their positive plates together and negative plates together and no external voltage is applied. what is the potential difference across each capacitor ?
4009V
8009V
400V
200V
The correct Answer is:B
To solve the problem step by step, we will follow these steps:
Step 1: Calculate the Effective Capacitance
When capacitors are connected in series, the effective capacitance Ceffective can be calculated using the formula:
1Ceffective=1C1+1C2
Given C1=10μF and C2=20μF:
1Ceffective=110+120=2+120=320
Thus,
Ceffective=203μF
Step 2: Calculate the Charge on the Capacitors
Using the formula Q=C×V, where V=200V:
Q=Ceffective×V=203×10−6×200
Calculating this gives:
Q=20×2003×10−6=40003×10−6=43×10−3C
Step 3: Reconnect the Capacitors
After disconnecting from the voltage source, the capacitors are reconnected with their positive plates together and negative plates together. The charge on each capacitor will redistribute.
Step 4: Define Charges on Capacitors
Let Q0=43×10−3C be the initial charge on each capacitor. When they are reconnected:
- The charge on the 10 µF capacitor becomes Q1=Q0−Q
- The charge on the 20 µF capacitor becomes Q2=Q0+Q
Step 5: Set Up the Voltage Equations
Since the capacitors are now in parallel, the voltage across each capacitor must be equal:
Q1C1=Q2C2
Substituting the values:
Q0−Q10×10−6=Q0+Q20×10−6
Cross-multiplying gives:
20(Q0−Q)=10(Q0+Q)
Expanding and simplifying:
20Q0−20Q=10Q0+10Q
10Q0=30Q⟹Q=13Q0
Step 6: Calculate Final Charges
Now we can find the final charges:
- For the 10 µF capacitor:
Q1=Q0−Q=Q0−13Q0=23Q0
- For the 20 µF capacitor:
Q2=Q0+Q=Q0+13Q0=43Q0
Step 7: Calculate the Potential Differences
Now we can find the potential difference across each capacitor:
- For the 10 µF capacitor:
V1=Q1C1=23Q010×10−6=23×43×10−310×10−6=8×10−330×10−6=830×103=415×103≈267V
- For the 20 µF capacitor:
V2=Q2C2=43Q020×10−6=43×43×10−320×10−6=16×10−360×10−6=1660×103=415×103≈267V
Summary of Results
The potential difference across the 10 µF capacitor is approximately 267V, and across the 20 µF capacitor is approximately 133V.
When capacitors are connected in series, the effective capacitance Ceffective can be calculated using the formula:
1Ceffective=1C1+1C2
Given C1=10μF and C2=20μF:
1Ceffective=110+120=2+120=320
Thus,
Ceffective=203μF
Using the formula Q=C×V, where V=200V:
Q=Ceffective×V=203×10−6×200
Calculating this gives:
Q=20×2003×10−6=40003×10−6=43×10−3C
After disconnecting from the voltage source, the capacitors are reconnected with their positive plates together and negative plates together. The charge on each capacitor will redistribute.
Let Q0=43×10−3C be the initial charge on each capacitor. When they are reconnected:
- The charge on the 10 µF capacitor becomes Q1=Q0−Q
- The charge on the 20 µF capacitor becomes Q2=Q0+Q
Since the capacitors are now in parallel, the voltage across each capacitor must be equal:
Q1C1=Q2C2
Substituting the values:
Q0−Q10×10−6=Q0+Q20×10−6
Cross-multiplying gives:
20(Q0−Q)=10(Q0+Q)
Expanding and simplifying:
20Q0−20Q=10Q0+10Q
10Q0=30Q⟹Q=13Q0
Now we can find the final charges:
- For the 10 µF capacitor:
Q1=Q0−Q=Q0−13Q0=23Q0
- For the 20 µF capacitor:
Q2=Q0+Q=Q0+13Q0=43Q0
Now we can find the potential difference across each capacitor:
- For the 10 µF capacitor:
V1=Q1C1=23Q010×10−6=23×43×10−310×10−6=8×10−330×10−6=830×103=415×103≈267V
V2=Q2C2=43Q020×10−6=43×43×10−320×10−6=16×10−360×10−6=1660×103=415×103≈267V
The potential difference across the 10 µF capacitor is approximately 267V, and across the 20 µF capacitor is approximately 133V.
Similar Questions
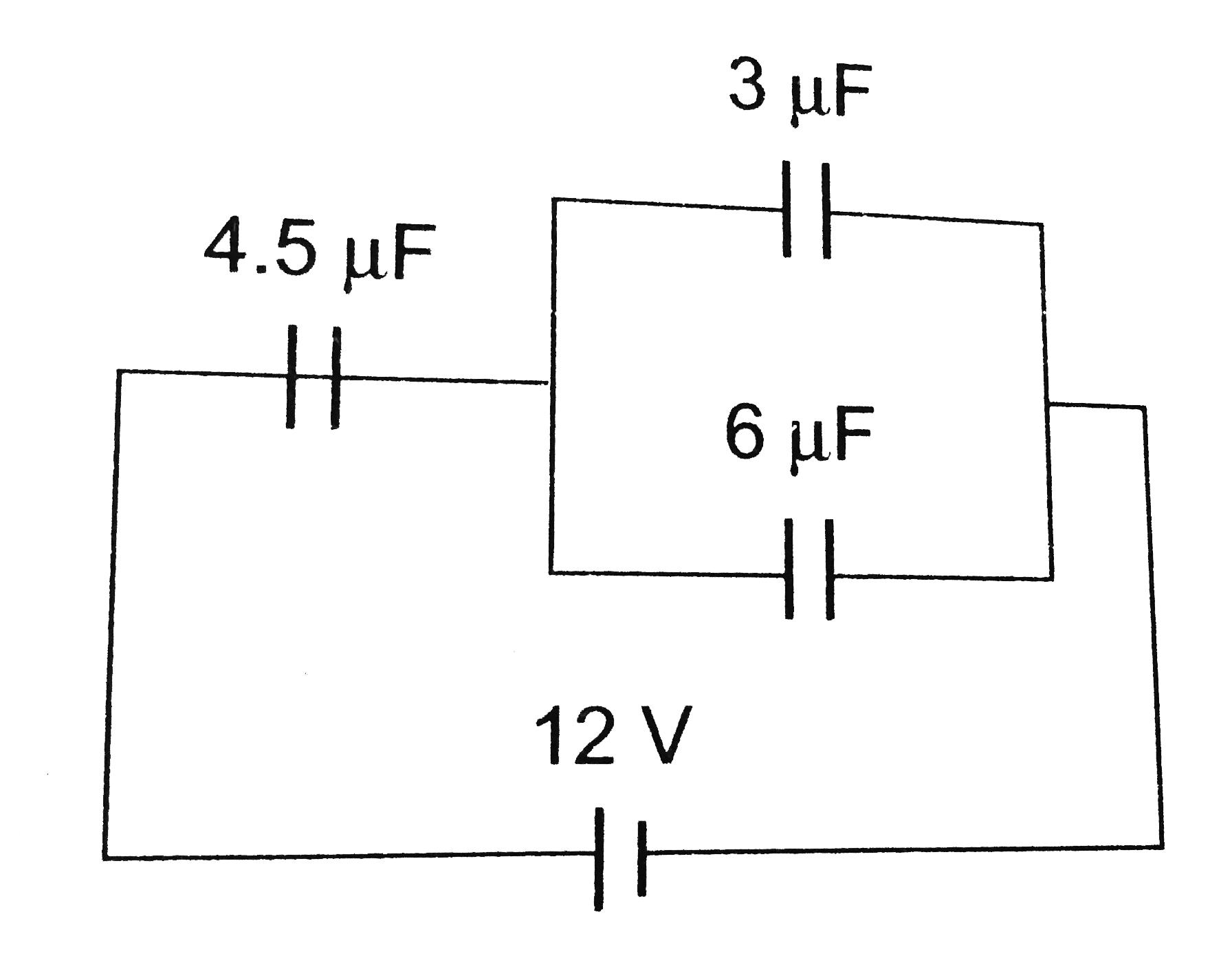
In the adjoning figure, the potential difference across the 4.5μF capacitor is

View Solutiongiven that potential differene across 1μF capacitor is 10V. Then,
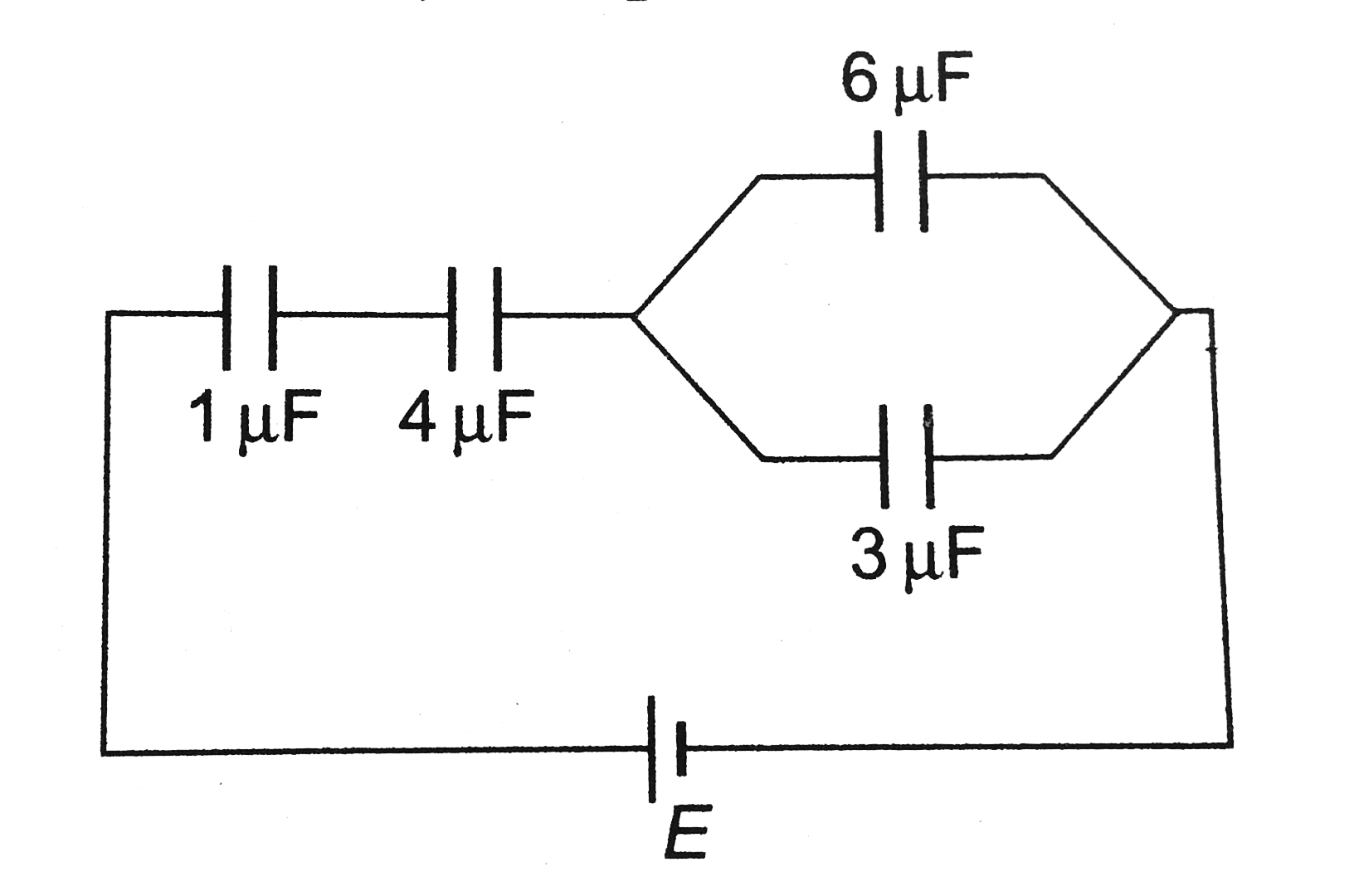
View SolutionWhat is the potential difference across 2μF capacitor in the circuit shown?
View SolutionIn the circuit shown in the figure, the potential difference across the 4.5μF capacitor is
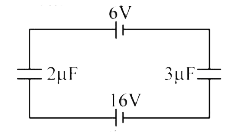
View SolutionThe potential drop across 7μF capacitor is 6V. Then
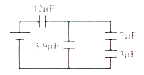
View SolutionA 1μF capacitor and a 2µF capacitor are connected in series across a 1200V supply line.
a. Find the charge on each capacitor and the voltage across them.
b. The charged capacitors are disconnected from the line and from each other and reconnected with terminals of like sign together. Find the final charge on each and the voltage across them.
View SolutionTwo capacitors of 10μF and 20μF are connected in series with a 30V battery. The charge on the capacitors will be, respectively
View SolutionIn the given circuit, the potential difference across the 6μF capacitor in steady state is
View SolutionA 4.00μF capacitor and a 6.00μF capacitor are connected in parallel across a 660V supply line
(a) Find the charge on each capacitor and the voltage across each.
(b) The charged capacitors are disconnected from the line and from each other, and reconnected to each other with terminals of unlike sign together. Find the final charge on each and the voltage across each.
View SolutionFigure shows five capacitors connected across a 12V power supply. What is the charge on the 2μF capacitor ?

View Solution
