A 4.00μF capacitor and a 6.00μF capacitor are connected in parallel across a 660V supply line
(a) Find the charge on each capacitor and the voltage across each.
(b) The charged capacitors are disconnected from the line and from each other, and reconnected to each other with terminals of unlike sign together. Find the final charge on each and the voltage across each.
The correct Answer is:A, B, C
Solution:
(a) To find the charge on each capacitor and the voltage across each:
1. Identify the capacitances and voltage:
- Capacitance of capacitor 1, C1=4.00μF=4.00×10−6F
- Capacitance of capacitor 2, C2=6.00μF=6.00×10−6F
- Voltage across both capacitors, V=660V
2. Calculate the charge on capacitor 1:
Q1=C1×V=4.00×10−6F×660V=2.64×10−3C=2640μC
3. Calculate the charge on capacitor 2:
Q2=C2×V=6.00×10−6F×660V=3.96×10−3C=3960μC
4. Voltage across each capacitor:
Since the capacitors are connected in parallel, the voltage across each capacitor is the same:
VC1=VC2=660V
Final Results for (a):
- Charge on capacitor 1, Q1=2640μC
- Charge on capacitor 2, Q2=3960μC
- Voltage across each capacitor, V=660V
---
(b) To find the final charge on each capacitor and the voltage across each after they are disconnected and reconnected with unlike terminals together:
1. Initial charges:
- Charge on capacitor 1, Q1=2640μC (positive)
- Charge on capacitor 2, Q2=−3960μC (negative)
2. Calculate the total charge when they are connected:
Qtotal=Q1+Q2=2640μC−3960μC=−1320μC
3. Let the final voltage across both capacitors be Vf.
- Charge on capacitor 1 after reconnection:
Q1f=C1×Vf=4.00×10−6F×Vf
- Charge on capacitor 2 after reconnection:
Q2f=C2×Vf=6.00×10−6F×Vf
4. Apply conservation of charge:
Qtotal=Q1f+Q2f
−1320μC=4.00×10−6F×Vf+6.00×10−6F×Vf
−1320μC=(4+6)×10−6F×Vf=10×10−6F×Vf
5. Solve for Vf:
Vf=−1320μC10×10−6F=−132V
6. Calculate final charges:
- Charge on capacitor 1:
Q1f=4.00×10−6F×(−132V)=−528μC
- Charge on capacitor 2:
Q2f=6.00×10−6F×(−132V)=−792μC
Final Results for (b):
- Final charge on capacitor 1, Q1f=−528μC
- Final charge on capacitor 2, Q2f=−792μC
- Final voltage across each capacitor, Vf=−132V
---
- Capacitance of capacitor 1, C1=4.00μF=4.00×10−6F
- Capacitance of capacitor 2, C2=6.00μF=6.00×10−6F
- Voltage across both capacitors, V=660V
Q1=C1×V=4.00×10−6F×660V=2.64×10−3C=2640μC
Q2=C2×V=6.00×10−6F×660V=3.96×10−3C=3960μC
Since the capacitors are connected in parallel, the voltage across each capacitor is the same:
VC1=VC2=660V
- Charge on capacitor 1, Q1=2640μC
- Charge on capacitor 2, Q2=3960μC
- Voltage across each capacitor, V=660V
- Charge on capacitor 1, Q1=2640μC (positive)
- Charge on capacitor 2, Q2=−3960μC (negative)
Qtotal=Q1+Q2=2640μC−3960μC=−1320μC
- Charge on capacitor 1 after reconnection:
Q1f=C1×Vf=4.00×10−6F×Vf
- Charge on capacitor 2 after reconnection:
Q2f=C2×Vf=6.00×10−6F×Vf
Qtotal=Q1f+Q2f
−1320μC=4.00×10−6F×Vf+6.00×10−6F×Vf
−1320μC=(4+6)×10−6F×Vf=10×10−6F×Vf
Vf=−1320μC10×10−6F=−132V
- Charge on capacitor 1:
Q1f=4.00×10−6F×(−132V)=−528μC
- Charge on capacitor 2:
Q2f=6.00×10−6F×(−132V)=−792μC
- Final charge on capacitor 1, Q1f=−528μC
- Final charge on capacitor 2, Q2f=−792μC
- Final voltage across each capacitor, Vf=−132V
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - CAPACITORSEXERCISE - OBJECTIVE_TYPE1videos
CAPACITORS
- BOOK - DC PANDEY ENGLISHCHAPTER - CAPACITORSEXERCISE - OBJECTIVE_TYPE1videos
CAPACITORS
- BOOK - DC PANDEY ENGLISHCHAPTER - ATOMSEXERCISE - MEDICAL ENTRANCES GALLERY42videos
ATOMS
- BOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective11videos
COMMUNICATION SYSTEM
Similar Questions
A 1μF capacitor and a 2µF capacitor are connected in series across a 1200V supply line.
a. Find the charge on each capacitor and the voltage across them.
b. The charged capacitors are disconnected from the line and from each other and reconnected with terminals of like sign together. Find the final charge on each and the voltage across them.View SolutionFind charge on each capacitor and potential difference across each capacitor .
 View Solution
View SolutionFind the charges on 6μF and 4μF capacitors
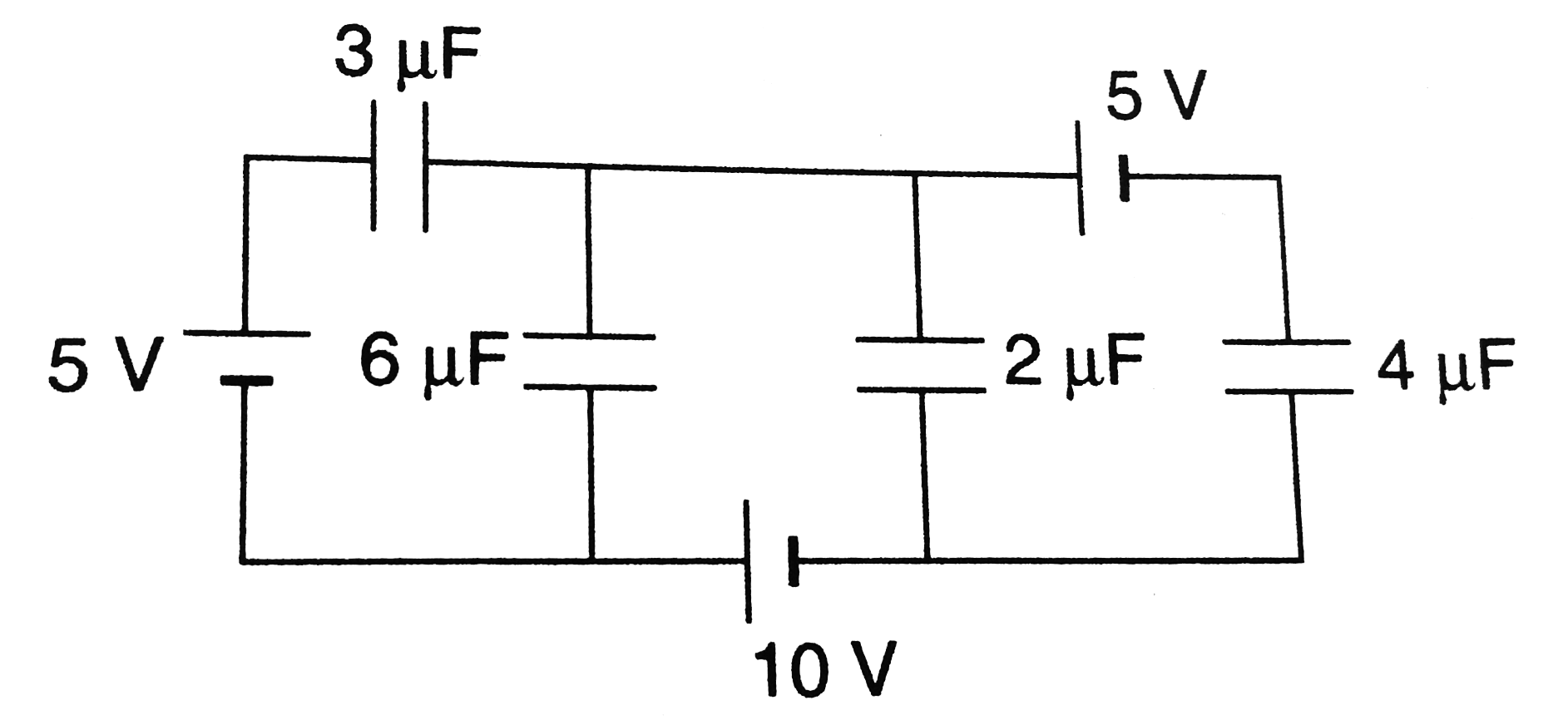 View Solution
View SolutionFigure shows five capacitors connected across a 12V power supply. What is the charge on the 2μF capacitor ?
 View Solution
View SolutionA 10μF capacitor and a 20μF capacitor are connected in series across a 200V supply line. The chraged capacitors are then disconnected from the line and reconnected with their positive plates together and negative plates together and no external voltage is applied. what is the potential difference across each capacitor ?
View SolutionA 10μF capacitor and a 20μF capacitor are connected in series across a 200V supply line. The chraged capacitors are then disconnected from the line and reconnected with their positive plates together and negative plates together and no external voltage is applied. what is the potential difference across each capacitor ?
View SolutionThree capacitors having capacitances of 8.4μF,8.4μF and 4.2μF are connected in series across a 36 potential difference.
(a) What is the charge on 4.2μF capacitor?
(b) What is the total energy stored in all three capacitors?
(c) The capacitors are disconnected from the potential difference without allowing them to discharge. They are then reconnected in parallel with each other, with the positively charged plates connected together. What is the voltage across each capacitor in the parallel combination?
(d) What is the total energy now stored in the capacitors?View SolutionHow many 1μF capacitors must be connected in parallel to store a charge of 1 C with a potential of 110 V across the capacitors?
View SolutionFind the potential difference and charge on each capacitor.
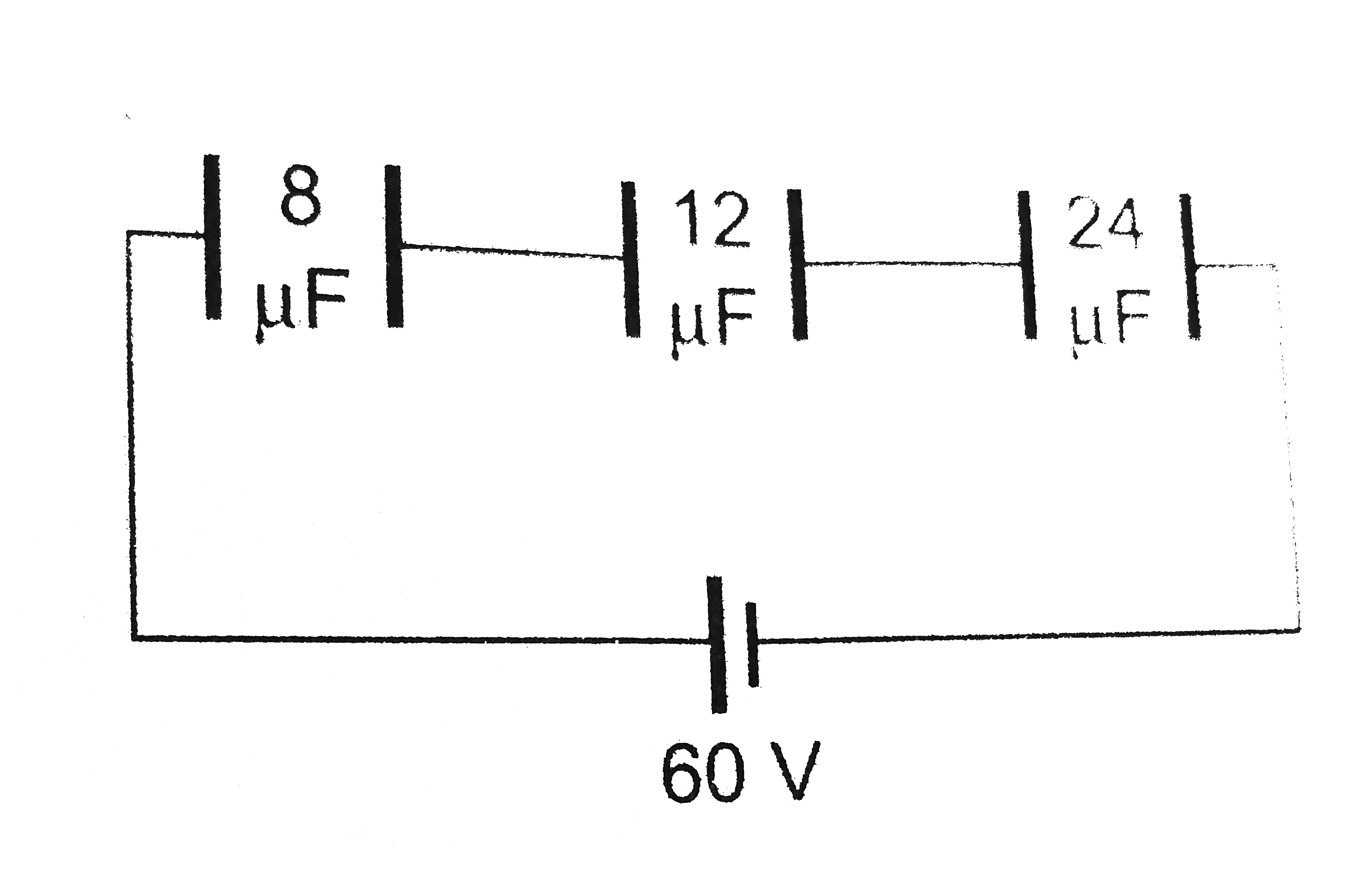 View Solution
View SolutionTwo capacitors 2μFand4μF are connected in parallel. A third capacitor of 6μF capacity is connected in series. The combination is connected across a 12 V battery. The voltage across a 2μF capacitor is
 View Solution
View Solution

