A straight section PQ of a circuit lies along the x-axis from x=−a2 to x=a2 and carries a steady current i. The magnetic field due to the section PQ at a point x =+a will be
proportional to a
proportional to a2
proportional to 1/a
zero
The correct Answer is:D
To solve the problem of finding the magnetic field due to a straight section PQ of a circuit at a point x = +a, we can follow these steps:
1. Understanding the Configuration:
- The straight section PQ lies along the x-axis from x=−a2 to x=a2.
- The point where we need to find the magnetic field is at x=a.
2. Using Biot-Savart Law:
- The Biot-Savart Law states that the magnetic field B at a point due to a current-carrying conductor is given by:
dB=μ04πIdl×rr3
- Here, I is the current, dl is the current element, and r is the position vector from the current element to the point where the field is being calculated.
3. Identifying the Geometry:
- For the straight section PQ, we can consider a small current element dl at a position x (where −a2≤x≤a2).
- The position vector r from the current element to the point x=a is r=a−x.
4. Calculating the Angle:
- The angle θ between the current element dl and the vector r is crucial for applying the Biot-Savart Law.
- Since the current flows along the x-axis and the point is also on the x-axis, the angle θ between dl and r is 0∘.
5. Evaluating the Magnetic Field:
- Since sin(0∘)=0, the contribution to the magnetic field from each current element dl becomes zero:
dB=μ04πIdl×rr3=0
- Therefore, the total magnetic field B at point x=a is also zero.
6. Conclusion:
- The magnetic field due to the straight section PQ at point x=a is:
B=0
Final Answer:
The magnetic field at point x=a is 0. Therefore, the correct option is option 4.
- The straight section PQ lies along the x-axis from x=−a2 to x=a2.
- The point where we need to find the magnetic field is at x=a.
- The Biot-Savart Law states that the magnetic field B at a point due to a current-carrying conductor is given by:
dB=μ04πIdl×rr3
- Here, I is the current, dl is the current element, and r is the position vector from the current element to the point where the field is being calculated.
- For the straight section PQ, we can consider a small current element dl at a position x (where −a2≤x≤a2).
- The position vector r from the current element to the point x=a is r=a−x.
- The angle θ between the current element dl and the vector r is crucial for applying the Biot-Savart Law.
- Since the current flows along the x-axis and the point is also on the x-axis, the angle θ between dl and r is 0∘.
- Since sin(0∘)=0, the contribution to the magnetic field from each current element dl becomes zero:
dB=μ04πIdl×rr3=0
- Therefore, the total magnetic field B at point x=a is also zero.
- The magnetic field due to the straight section PQ at point x=a is:
B=0
The magnetic field at point x=a is 0. Therefore, the correct option is option 4.
Topper's Solved these Questions
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - single correct Ansewer type
12 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Subjective type
10 Videos
- RAY OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RAY OPTICSEXERCISE - DPP 1.6
12 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Comprehension Type
14 Videos
Similar Questions
A straight section PQ of a circuit lise along the X-axis from x=−a2 to x=a2 and carriers a steady current i. The magnetic field due to the section PQ at a point X=+a will be
View SolutionMagnetic field at point O due to straight conductor PQ is
_PHY_E06_180_Q01.png)
View SolutionThe figure shows the cross-section of a long cylindrical conductor of radius a carrying a uniformly distributed current i. The magnetic field due to current at P is :
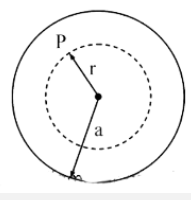
View SolutionA long straight wire of a circular cross-section of radius 'a' carries a steady current I. The current is uniformly distributed across the cross-section. Apply Ampere's circuital law to calculate the magnetic field at a point at distance 'r' in the region for (i) r<a and (ii) r>a.
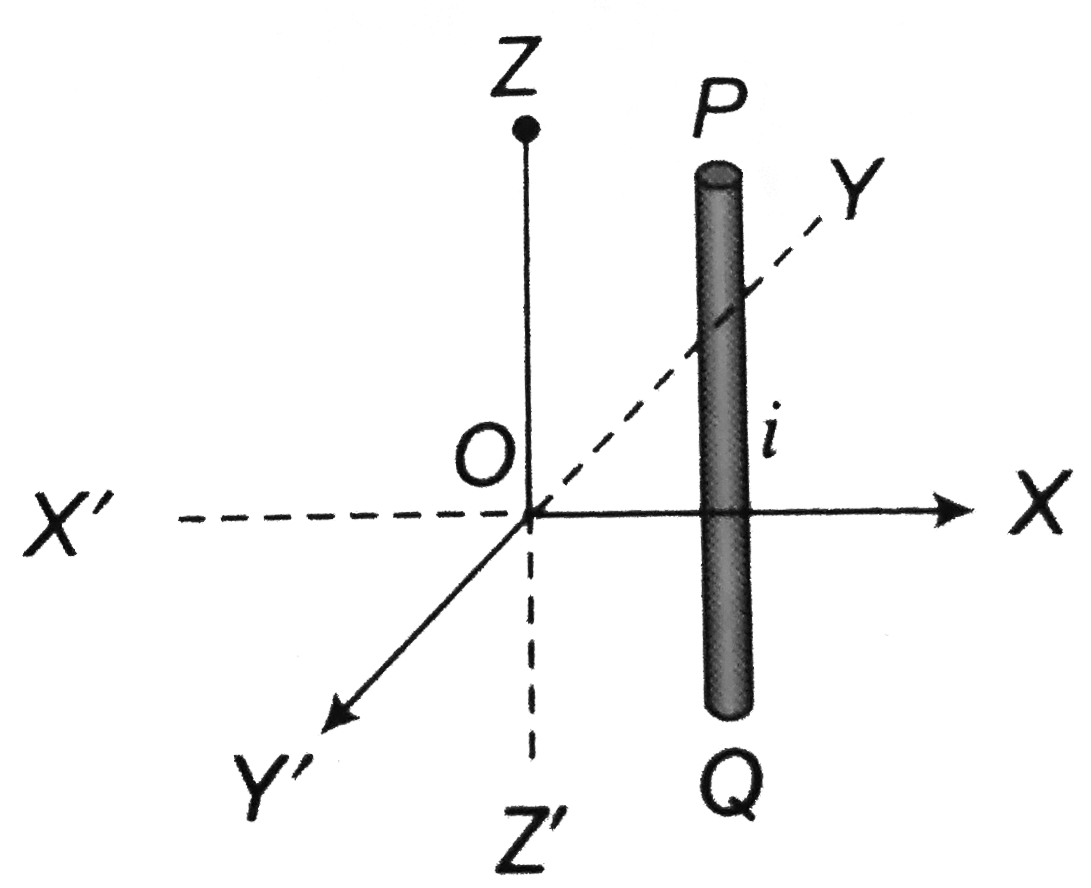
View SolutionA vertical wire kept in Z−X plane carries a current from Q to P (see figure). The magnetic field due to current will have the direction at the origin O along
View SolutionA long straight wire of a curcular cross-section of radius 'a' carries a steady current 'l'. The current is uniformly distributed the across- section . Apply Amphere's circuital law to calculate the magnetic field at a point 'r' in the region for (i) r<a and (ii) r>a.
View SolutionA long straight wire of a circular cross section (radius a) carrying steady current. Current is uniformly distributed in the wire. Calculate magnetic field inside the region (r<a) in the wire.
View SolutionFigure shows a long straight wire of a circular cross-section (radius a) carrying steady current l. The current l is uniformly distributed across this cross-section. Calculate the magnetic field in the region r<aandr>a

View SolutionA long straight wire along the z- axis carries a current I in the negative z−direction . The magnetic vector field →B at a point having coordinates (x,y) in the Z=0 plane is
View SolutionA long straight wire along the z- axis carries a current I in the negative z−direction . The magnetic vector field →B at a point having coordinates (x,y) in the Z=0 plane is
View Solution
