A straight section PQ of a circuit lise along the X-axis from x=−a2 to x=a2 and carriers a steady current i. The magnetic field due to the section PQ at a point X=+a will be
∝a
zero
∝a2
∝1a
The correct Answer is:B
To find the magnetic field at point X=+a due to the straight section PQ of the circuit carrying a steady current i, we can use the Biot-Savart Law. The magnetic field B due to a current-carrying conductor can be calculated using the formula:
B=μ04π∫idl×^rr2
where:
- μ0 is the permeability of free space,
- i is the current,
- dl is the differential length element of the conductor,
- ^r is the unit vector from the current element to the point where the field is being calculated,
- r is the distance from the current element to the point.
Step 1: Define the Geometry
The section PQ lies along the x-axis from x=−a2 to x=a2. We need to find the magnetic field at the point x=a.
Step 2: Set Up the Integral
The differential length element dl can be expressed as dx along the x-axis. The position vector from a point on the conductor to the point x=a is given by r=a−x.
Step 3: Calculate the Distance and Unit Vector
The distance r from the current element at position x to the point x=a is:
r=a−x
The unit vector ^r pointing from the current element to the point x=a is:
^r=(a−x)^i|a−x|=^i(since a−x>0 for x<a)
Step 4: Apply the Biot-Savart Law
Now, substituting into the Biot-Savart Law, we have:
B=μ0i4π∫a2−a2dx^i×^i(a−x)2
Since ^i×^i=0, the entire integral evaluates to zero:
B=0
Conclusion
Thus, the magnetic field at the point x=a due to the straight section PQ of the circuit carrying a steady current i is:
B=0
Final Answer
The magnetic field at the point X=+a is 0.
---
- μ0 is the permeability of free space,
- i is the current,
- dl is the differential length element of the conductor,
- ^r is the unit vector from the current element to the point where the field is being calculated,
- r is the distance from the current element to the point.
The section PQ lies along the x-axis from x=−a2 to x=a2. We need to find the magnetic field at the point x=a.
The differential length element dl can be expressed as dx along the x-axis. The position vector from a point on the conductor to the point x=a is given by r=a−x.
The distance r from the current element at position x to the point x=a is:
r=a−x
^r=(a−x)^i|a−x|=^i(since a−x>0 for x<a)
Now, substituting into the Biot-Savart Law, we have:
B=μ0i4π∫a2−a2dx^i×^i(a−x)2
B=0
Thus, the magnetic field at the point x=a due to the straight section PQ of the circuit carrying a steady current i is:
B=0
The magnetic field at the point X=+a is 0.
Topper's Solved these Questions
Similar Questions
A straight section PQ of a circuit lies along the x-axis from x=−a2 to x=a2 and carries a steady current i. The magnetic field due to the section PQ at a point x =+a will be
View SolutionMagnetic field at point O due to straight conductor PQ is
_PHY_E06_180_Q01.png) View Solution
View SolutionThe figure shows the cross-section of a long cylindrical conductor of radius a carrying a uniformly distributed current i. The magnetic field due to current at P is :
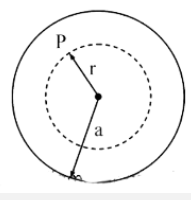 View Solution
View SolutionA long straight wire of a circular cross-section of radius 'a' carries a steady current I. The current is uniformly distributed across the cross-section. Apply Ampere's circuital law to calculate the magnetic field at a point at distance 'r' in the region for (i) r<a and (ii) r>a.
View SolutionA long straight wire of a curcular cross-section of radius 'a' carries a steady current 'l'. The current is uniformly distributed the across- section . Apply Amphere's circuital law to calculate the magnetic field at a point 'r' in the region for (i) r<a and (ii) r>a.
View SolutionA long straight wire of a circular cross section (radius a) carrying steady current. Current is uniformly distributed in the wire. Calculate magnetic field inside the region (r<a) in the wire.
View SolutionFigure shows a long straight wire of a circular cross-section (radius a) carrying steady current l. The current l is uniformly distributed across this cross-section. Calculate the magnetic field in the region r<aandr>a
 View Solution
View SolutionA long straight wire along the z- axis carries a current I in the negative z−direction . The magnetic vector field →B at a point having coordinates (x,y) in the Z=0 plane is
View SolutionA long straight wire along the z- axis carries a current I in the negative z−direction . The magnetic vector field →B at a point having coordinates (x,y) in the Z=0 plane is
View SolutionThe wire shown in Fig. carries current I in the direction shown. The wire consists of a very long, straight section, a quarter- circle with radius R, and another long, straight section. What are magnitude and direction of net magnetic field at the center of curvature of quarter-circle section (point P)?
 View Solution
View Solution

