A glass hemisphere of radius 0.04 m and refractive index of the material 1.6 is placed centrally over cross mark on a paper (i) with the flat face, (ii) with the curved face in contact with the paper. In each case, the cross mark is viewed directly from above. The position of the images will be
0.04 m from the flat face, (ii) 0.025 m from the flat face
(i) At the same position of the cross mar, (ii)0.025 m below the flat face
(i) 0.025 m from the flat face, (ii) 0.04 m from the flat face
For both (i) and (ii) 0.025 m from the highest point of the hemisphere
The correct Answer is:B
To solve the question step by step, we will analyze both cases of the glass hemisphere:
Case (i): Flat face in contact with the paper
1. Identify the parameters:
- Radius (R) = 0.04 m
- Refractive index of glass (μ1) = 1.6
- Refractive index of air (μ2) = 1 (since we are viewing from air)
2. Use the lens maker's formula:
The formula we will use is:
μ2V−μ1U=μ2−μ1R
Here, U is the object distance (from the curved surface to the object), which is equal to -0.04 m (negative because it is measured in the opposite direction).
3. Substituting values:
1V−1.6−0.04=1−1.60.04
This simplifies to:
1V+40=−0.60.04
1V+40=−15
1V=−15−40=−55
V=−155≈−0.01818 m
4. Interpret the result:
The negative sign indicates that the image is formed on the same side as the object, which means the image is at the position of the cross mark (0.04 m from the flat surface).
Case (ii): Curved face in contact with the paper
1. Identify the parameters:
- Radius (R) = 0.04 m
- Refractive index of glass (μ1) = 1.6
- Refractive index of air (μ2) = 1
2. Use the formula for apparent depth:
The relationship between real depth (h) and apparent depth (h') is given by:
μ=hh′
Rearranging gives:
h′=hμ
3. Substituting values:
h′=0.041.6=0.025 m
4. Interpret the result:
The apparent depth is 0.025 m, meaning the image of the cross mark will appear to be at a depth of 0.025 m from the curved surface.
Summary of Results:
- For the flat face in contact with the paper, the image position is at 0.04 m.
- For the curved face in contact with the paper, the image position is at 0.025 m.
- Radius (R) = 0.04 m
- Refractive index of glass (μ1) = 1.6
- Refractive index of air (μ2) = 1 (since we are viewing from air)
The formula we will use is:
μ2V−μ1U=μ2−μ1R
Here, U is the object distance (from the curved surface to the object), which is equal to -0.04 m (negative because it is measured in the opposite direction).
1V−1.6−0.04=1−1.60.04
This simplifies to:
1V+40=−0.60.04
1V+40=−15
1V=−15−40=−55
V=−155≈−0.01818 m
The negative sign indicates that the image is formed on the same side as the object, which means the image is at the position of the cross mark (0.04 m from the flat surface).
- Radius (R) = 0.04 m
- Refractive index of glass (μ1) = 1.6
- Refractive index of air (μ2) = 1
The relationship between real depth (h) and apparent depth (h') is given by:
μ=hh′
Rearranging gives:
h′=hμ
h′=0.041.6=0.025 m
The apparent depth is 0.025 m, meaning the image of the cross mark will appear to be at a depth of 0.025 m from the curved surface.
- For the flat face in contact with the paper, the image position is at 0.04 m.
- For the curved face in contact with the paper, the image position is at 0.025 m.
Topper's Solved these Questions
- RAY OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RAY OPTICSEXERCISE - DPP 1.4
15 Videos
- RAY OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RAY OPTICSEXERCISE - DPP 1.5
13 Videos
- RAY OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RAY OPTICSEXERCISE - DPP 1.2
15 Videos
- PHOTOELECTRIC EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PHOTOELECTRIC EFFECTEXERCISE - Integer Type
4 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - single correct Ansewer type
12 Videos
Similar Questions
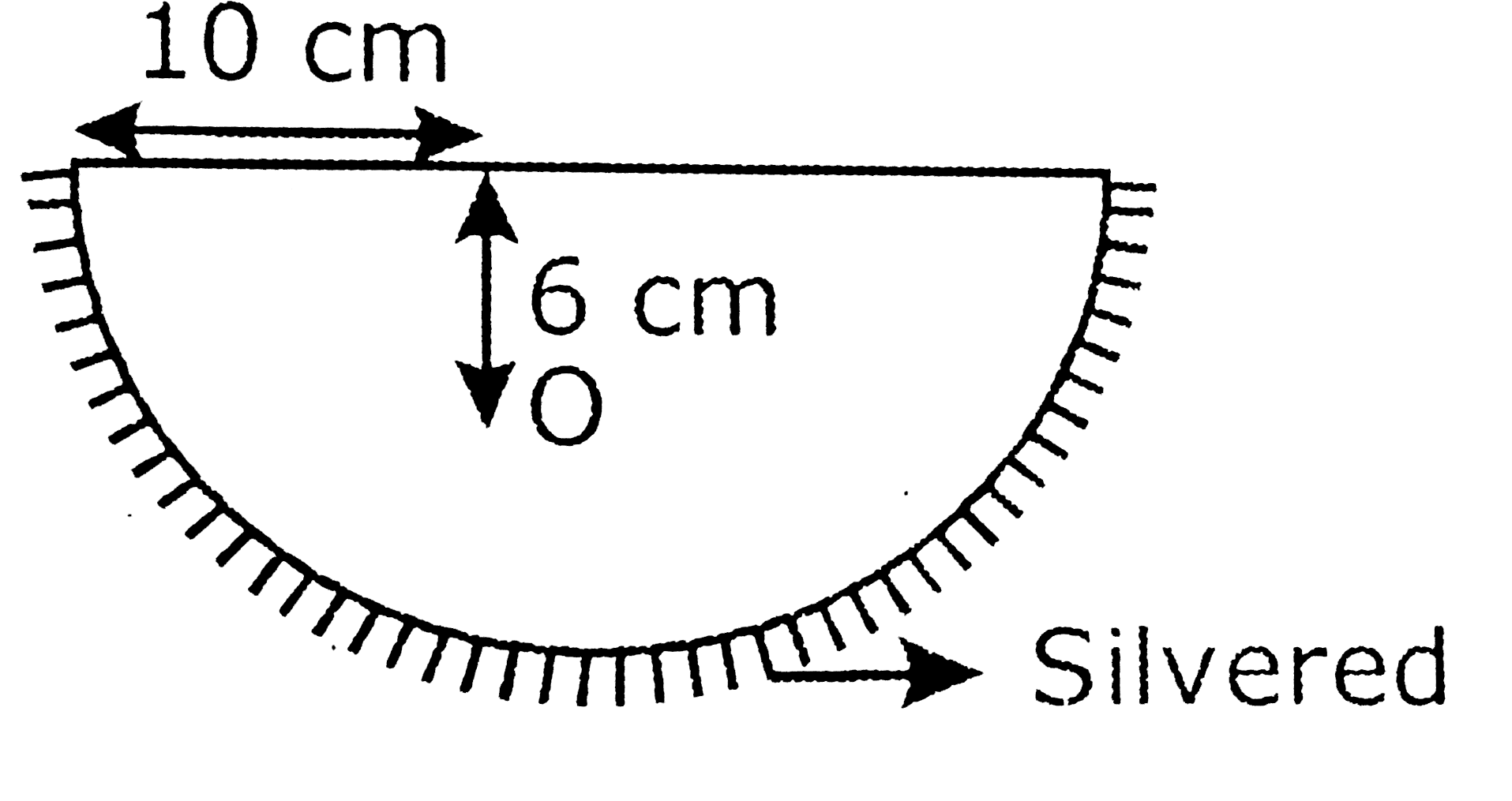
A hemispherical glass body of radius 10 cm and refractive index 1.5 is silvered on its curved surface . A small air bubble is 6 cm below the flat surface inside it along the axis. The position of the image of the air bubble made by the mirror is seen :
View SolutionA glass sphere has radius of 5.0cm and a refractive index of 1.6. A paperweight is constructed by slicing through the sphere on a plate that is 2.0cm from the centre of the sphere and perpendicular to radius of the sphere that passes through the centre of the circle formed by the intersection of the plane and the sphere. The paperweight is placed on a table and viewed from directly above an observer who is 8.0cm from the table top, as shown in figure. When viewed through the paperweight, how far away does the table top appear to the observer?
View Solution
Knowledge Check
A mark placed on the surface of a sphere is viewed through glass from a position directly opposite. If the diameter of the sphere is 10cm and refractive index of glass is 1.5, find the position of the image.
A−20cmB30cmC40cmD−10cm
A glass hemisphere of radius R and of material having refractive index 1.5 is silvered on its flat face as shown in figure., A small object of height h is located at a distance 2R from the surface of hemisphere as shown in the figure. The final image will form.

View SolutionA solid glass sphere with radius R and an index of refraction 1.5 is silvered over one hemisphere. A small object is located on the axis of the sphere at a distance 2R to the left of the vertex of the unsilvered hemisphere. Find the position of final image after all refractions and reflection have taken place.
View SolutionA monochromatic light of λ=500nm is incident on two identical slits separated by a distance of 5×10−4m. The interference pattern is seen on a screen placed at a distance of 1m from the plane of slits. A thin glass plate of thickness 1.5×10−6m and refractive index μ=1.5 is placed between one of the slits and the screen. Find the intensity at the center of the screen if the intensity is I0 in the absence of the plate. Also find the lateral shift of the central maxima and number of fringes crossed through center.
View SolutionA cylinderical glass rod of radius 0.1m and refractive index √3 lies on a horizontal plane mirror. A horizontal ray of light moving perpendicular to the axis of the rod is incident on it. At what height from the mirror should the ray be incident so that it leaves the rod at a height of 0.1m above the plane mirror? At what centre to centre distance a second similar rod, parallel to the first, be placed on the mirror, such that the emergent ray from the second rod is in line with the incident ray on the first rod?

View SolutionA plastic hemisphere has a radius of curvature of 8 cm and an index of refraction of 1.6. ON the axis halfway between the plane surface and the spherical one (4 cm from each) is a small object O. The distance between the two images when viewed along the axis from the two sides of the hemisphere is approximately
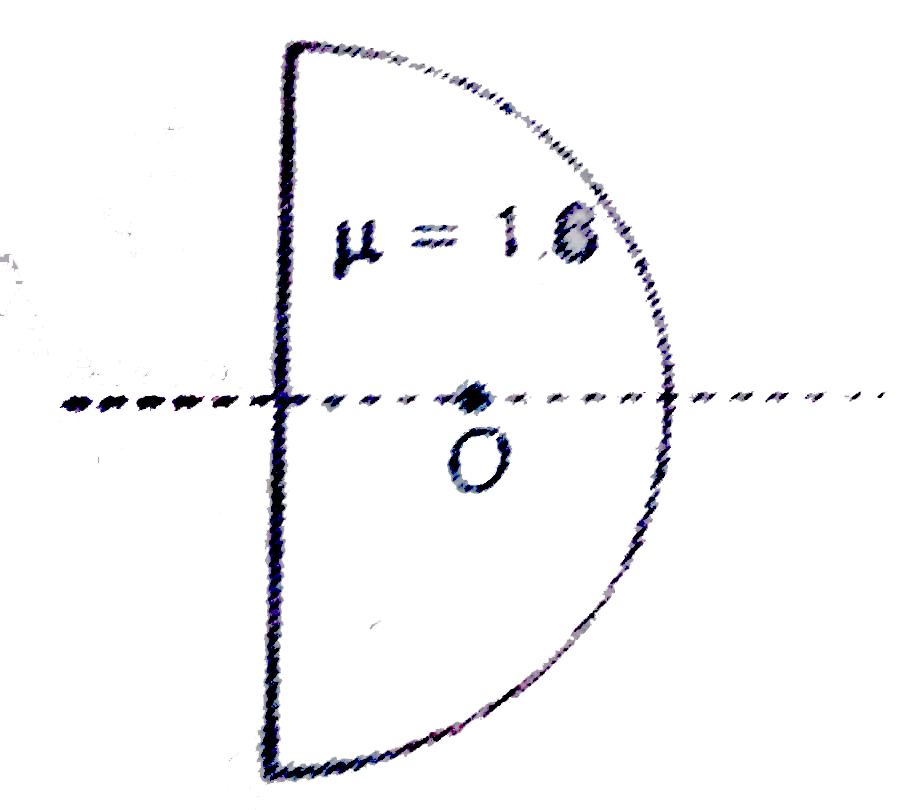
View SolutionA plastic hemisphere has a radius of curvature of 8cm and an index of refraction of 1.6. On the axis halfway between the plane surface and the spherical one (4cm from each) is a small object O.
The distance between the two images when viewed along the axis from the two sides of the hemisphere is approximately.

View SolutionA glass hemisphere of radius 10cm and μ=1.5 is silvered over its curved surface. There is an air bubble in the glass 5cms from the plane surface along the axis. Find the position of the images of this bubble seen by observer looking along the axis into the flat surface of the atmosphere.
View Solution
