Question

Draw the radial prodabilirty distritation corve for $2p$ ans $2s$ elelctron orbitals and compare them

Explanation

To draw the radial probability distribution curves for the 2s and 2p electron orbitals and compare them, we will follow these steps:

Step 1: Understand the Concept of Radial Probability Distribution
The radial probability distribution describes the likelihood of finding an electron at a certain distance from the nucleus in an atom. It is calculated by considering the volume of a spherical shell at a distance r from the nucleus.

Step 2: Draw the Radial Probability Distribution for 2s Orbital
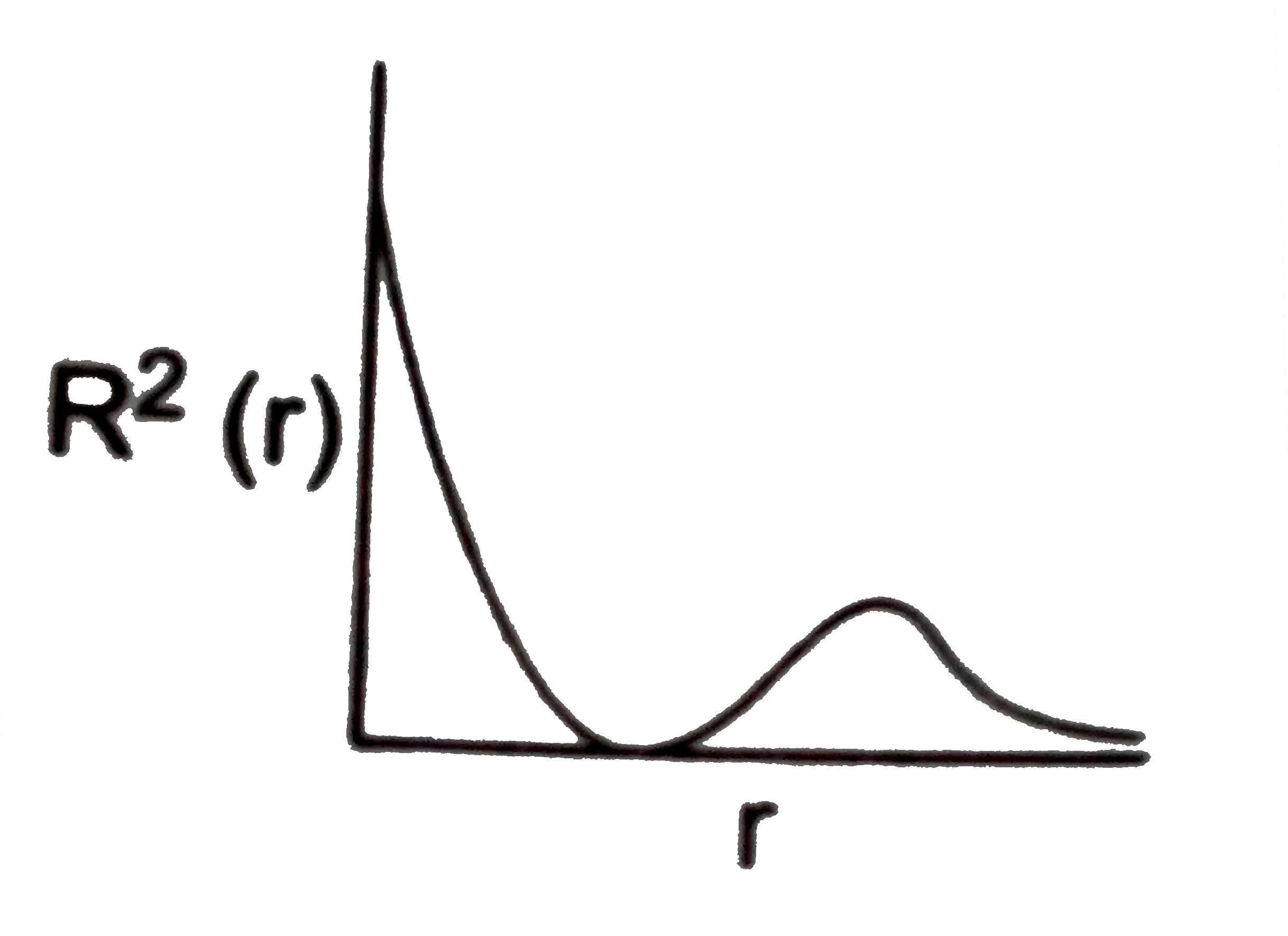
1. Shape of the Curve: The radial probability distribution curve for the 2s orbital has a characteristic shape with two peaks (maxima) and a node (a point where the probability is zero).
2. Label the Axes: The x-axis represents the distance from the nucleus (r), and the y-axis represents the radial probability density.
3. Draw the Curve: Start at the origin (0,0), rise to the first maximum, drop to zero at the node (where r is at a certain distance), then rise again to the second maximum.

Step 3: Draw the Radial Probability Distribution for 2p Orbital
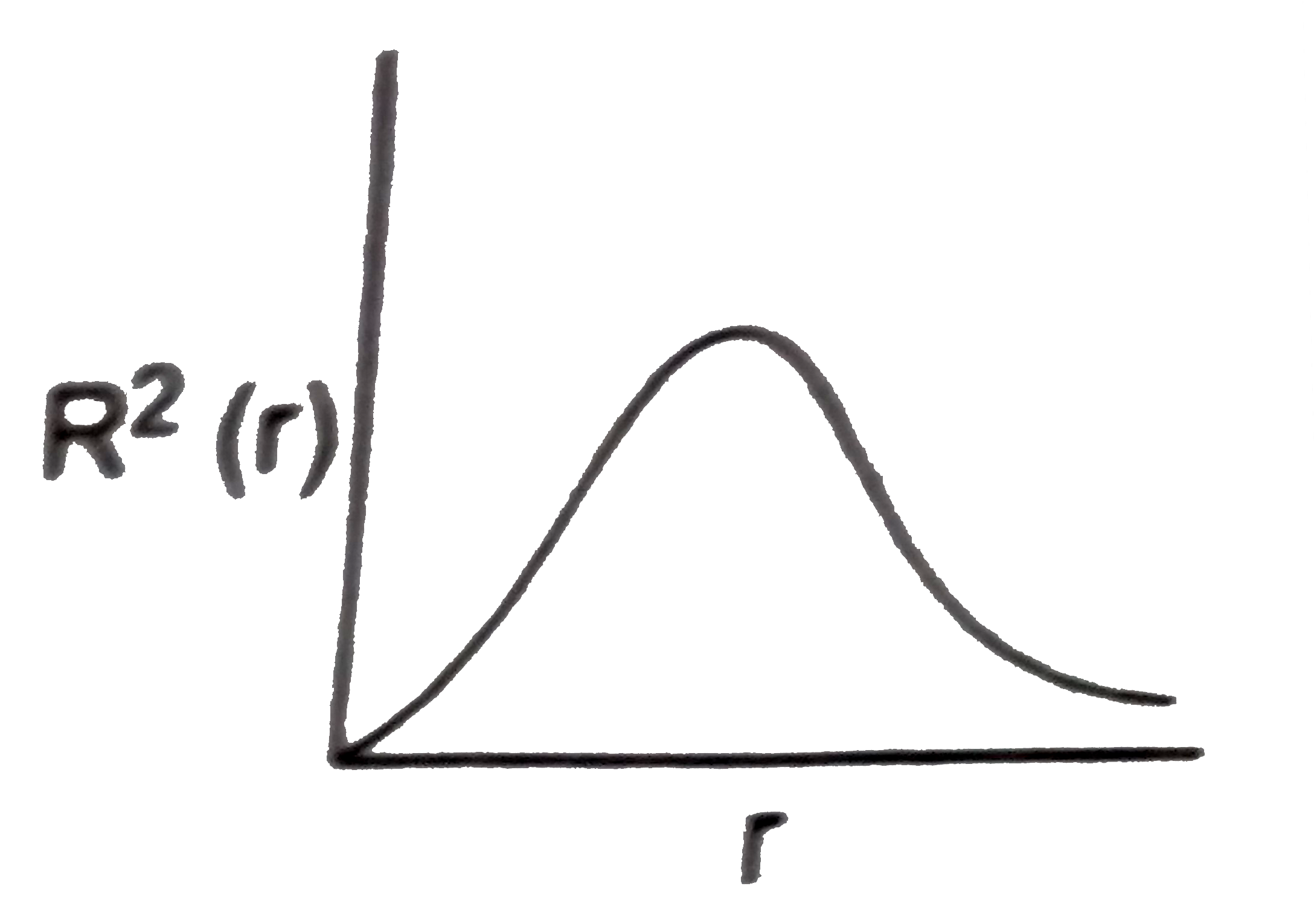
1. Shape of the Curve: The radial probability distribution curve for the 2p orbital has one peak (maximum) and does not have a node.
2. Label the Axes: Similar to the 2s orbital, the x-axis is the distance from the nucleus (r), and the y-axis is the radial probability density.
3. Draw the Curve: Start at the origin (0,0), rise to the maximum, and then gradually decrease as you move away from the nucleus.

Step 4: Compare the Two Curves
1. Number of Maxima: The 2s orbital has two maxima, while the 2p orbital has only one maximum.
2. Node Presence: The 2s orbital has a node (point of zero probability), while the 2p orbital does not have any nodes.
3. Probability Distribution: The 2s orbital shows a more complex distribution with regions of high and low probability, whereas the 2p orbital has a more uniform distribution around its maximum.

Step 5: Conclusion
The radial probability distribution curves for the 2s and 2p orbitals illustrate the differences in electron distribution around the nucleus. The 2s orbital has two peaks and a node, indicating regions of high and zero probability, while the 2p orbital has one peak with no nodes, indicating a more consistent probability of finding the electron.

---